前回、令和元年度秋の応用情報午前の計算問題解説を書いた。
そのまま、過去に向かって解説していくこととしよう。
というわけで、今回の解説対象は「平成31年度 春季 応用情報技術者試験 午前」の計算問題だ。
前回と同じく、かなりの長さになると思うので問題文はここには書かない。
上のリンクから実際の問題に飛べるので、そちらを参照してほしい。
また、誤りがあったら教えていただければ幸いだ。
では、始めていこう。
問1
2進数の演算の問題。
先に、255と256を2進数に直してみよう。
まず、255は1111 1111、256は1 0000 0000となる。
これらと、n+1を演算した場合を考えてみよう。
アについてはn+1が255以下の場合にはn+1が、256の場合は0となるので正しい。
ということで、いきなり答えが出てしまったが、アが正解だ。
他の選択肢についても見てみよう。
イについて、256とANDを取ると、n+1が255以下の場合には0、256の場合には256となってしまうので不適。
ウについて、n+1が255以下の場合に必ず255となってしまうので不適。
エについて、これもぱっと見は正しそうだが、実はn+1が256の時は256、それ未満の場合は256を加算した結果になってしまう。
よって、消去法でもアが選択できる。
なお、具体的な数字で計算してみるのも手だ。
例えば、n=1なんかの簡単な数字で試してみるといいだろう。
問6
シェルソートの問題。
…とはいったものの、アルゴリズムをしっかり読み取れば、シェルソート自体が何なのか分からなくても問題ない。
手順が4つあり、そのうちの3つ目を何回実行するか、というのが問題だ。
というわけで、具体的に処理を追ってみる。
まず、(1)で変数\(H\)にデータ数÷3の整数部分を代入する。
データの個数を数えると9個なので、\(H\)には3が代入される。
次に、(2)で並び替えが行われる。
そして、(3)で、\(H\)を3で割った整数部分を\(H\)に代入しなおす。
今、\(H = 3\)なので、ここで\(H\)は1に置き換わる。
(4)で、今\(H\)は0ではないので、(2)に戻ろう。
(2)で再度整列が行われ、(3)に進む。
ここで、\(H\)には1が入っており、1÷3の整数部分は0なので、\(H\)に0が代入される。
(4)で\(H\)が0なので整列完了、というわけだ。
ここで、(1)~(4)の処理の順番を改めて並べてみると、(1)→(2)→(3)→(4)→(2)→(3)→(4)となっている。
(3)は2回行われているので、答えはアだ。
ちなみに、シェルソートに関しては過去に本ブログで解説している。
理解を深めたかったら、以下の記事も参考にしてみてほしい。
問9
ちょっとややこしい。
データを別のアドレスにまとめて転送するとき、どんな情報を渡せばいいか、という問題だ。
先に、方向から見ていこう。
まず、アドレスの昇順で転送しようとすると、1001の内容が1003へ、1002の内容が1004へ、と転送されていく。
…のだが、この次、1003の内容を転送しようとしたとき、すでに1001だった内容が入ってしまっている。
そのため、昇順で転送しようとするとデータが消失してしまうので、不適。
この時点で方向フラグは1になり、選択肢はイかエのどちらかだ。
ここで、転送元のアドレスを、転送される順番に並び替えると、1004、1003、1002、1001となる。
つまり、最初に1004を転送しなければいけないので、選択肢のエが正解になる。
単純に、どこから(1004)、どちらの方向に向かうのか(小さい方に向かって)を考えればいい。
問10
転送速度の計算問題だ。
まず、バス幅が16ビット、メモリサイクルタイムが80ナノ秒とのことなので、80ナノ秒ごとに16ビットのデータを送れる。
単位を直しておこう。
聞かれている数値の単位がバイト/秒なので、16ビットを2バイト、80ナノ秒を\(80 \times 10^{-9}\)秒としておく。
そうすると、1回の送信で2バイト、それが\(80 \times 10^{-9}\)秒ごとに行われる。
先に、1秒間の回数を出しておこう。
これは、単純に\(1 \div (80 \times 10^{-9})\)で求められる。
それに、1回分の容量2バイトを掛ければいいので、
$$\frac{2}{80 \times 10^{-9}} = 25 \times 10^6$$
と求めることができる。
聞かれているのが何Mバイト/秒か、かつ1Mは\(10^6\)なので、答えは25Mバイト/秒、イが正解だ。
問12
…正直、計算問題に入れるか迷ったが、一応入れてみた。
タイムアウトの設定について、長い順に並べろという問題。
これは、実際の処理の流れを考えてみよう。
- まず、WebサーバがAPサーバへリクエストを送る。
- 次に、APサーバが処理を開始する。
- APサーバは、必要に応じてDBサーバへトランザクションなどの処理を要求する。
- APサーバが処理を終了したら、Webサーバへレスポンスを返す。
- Webサーバが、APサーバからのレスポンスを受け取る。
さて、では①から③のタイムアウトが、処理のどこにあたるかを見ていく。
まず、①はAPに関する処理なので、2~4までの処理部分がこの時間に含まれる。
次に、②はDBに関する処理を見ているので、3の処理だけだ。
最後、③はWebサーバなので、1~5の全ての処理分が含まれている。
よって、長い順に③、①、②で設定する必要があるので、答えはウだ。
タイムアウト云々よりも、処理の流れを理解できているか、という問題だろう。
問13
よくある稼働率の問題。
先に、直列と並列それぞれの稼働率の求め方をおさらいしておこう。
直列の場合は、両方が稼働していなければいけないので、両者の稼働率を掛け合わせたものが全体の稼働率になる。
つまり、稼働率\(r_1\)、\(r_2\)のシステムが直列で繋がっている場合、全体の稼働率\(R\)は
$$R = r_1 \times r_2$$
で表される。
それに対し、並列の場合はどちらか一方だけ稼働していればいいので、1から両方とも稼働していない状態を引くことで求める。
よって、稼働率\(r_1\)、\(r_2\)のシステムが並列で繋がっている場合、全体の稼働率\(R\)は
$$R = 1 – (1 – r_1)(1 – r_2)$$
で表される。
念のため、\(1 – r_1\)、\(1 – r_2\)はそれぞれが稼働していない率、それを掛けることで両者とも稼働していない率を求めることができる。
それを1から引けば、最低でもどちらか一方が稼働している部分を求めることができるのだ。
さて、というわけで問題を見てみよう。
今、全ての装置の稼働率は同じなので、一旦\(r\)としておこう。
まず、Aは単純な並列なので、稼働率\(R_A\)は
$$R_A = 1 – (1 – r)^2$$
となる。
次に、Bについて、並列部分を稼働率\(1 – (1 – r)^2\)の装置と見なすと、直列で繋がっているので、
$$R_B = r \times (1 – (1 – r)^2)$$
となる。
最後に、Cは直列になったものが並列で繋がっているので、
$$R_C = 1 – (1 – r^2)^2$$
となる。
さて、この大小関係を調べたいのだが、具体的な数を入れて計算してしまおう。
\(r = 0.9\)として、それぞれ計算すると、
$$R_A = 1 – (1 – 0.9)^2 = 0.99$$
$$R_B = 0.9 \times (1 – (1 – 0.9)^2) = 0.891$$
$$R_C = 1 – (1 – 0.9^2)^2 = 0.9639$$
ということで、高い順に並び替えると、A、C、Bとなり、イが正解だ。
このように、稼働率が高いものを選ぶ問題の場合、途中まで式をつくり、あとは具体的な数字を入れて計算すれば求めることができる。
多分式同士の比較でも大小関係くらいは求められると思うが、大変なので具体的な数字で確かめていこう。
問14
式さえ立てられれば簡単な問題だ。
まず、今のキャッシュサーバでのヒット率を求めなければいけない。
というわけで、それを0以上1未満の数\(x\)とし、今の平均検索応答時間に関する方程式を作る。
割合\(x\)で0.2秒、割合\(1-x\)で2.2秒かかり、平均で1秒なので…
$$0.2x + 2.2(1 – x) = 1$$
という式を作ることができる。
これを\(x\)について解くと、\(x = 0.6\)となる。
3年後、ヒット率は半分になるので、0.3だ。
それぞれのかかる秒数は変化しないので、あとは計算だ。
$$0.2 \times 0.3 + 2.2 \times (1 – 0.3) = 1.6$$
よって、1.6秒となるので、ウが正解だ。
問15
処理能力の計算問題。
先に計算の方針を書いておくと、まずサーバ、ネットワークそれぞれにおける、1秒間に処理できる件数を求める。
で、それぞれのうち、少ない件数の方が、最終的な処理件数となる。
サーバばかり高性能でも、ネットワークがいっぱいでは処理が届かない。
逆に、ネットワークが高速でも、サーバの性能以上は処理ができない。
だから、少ない方が処理できる上限になるのだ。
というわけで、まずはサーバ観点で見ていこう。
サーバの処理能力は100MIPS、つまり1秒間に100M回の命令を実行できる。
今、1件で100万命令あると書かれており、100万が1Mなので、1秒間に100件処理できることになる。
次に、ネットワークの観点。
転送速度が\(8 \times 10^7\)ビット/秒、バイト単位に直すと\(10^7\)バイト/秒だ。
1件のデータで\(2 \times 10^5\)バイトの容量があるということなので、計算していこう。
$$\frac{10^7}{2 \times 10^5} = 50$$
というわけで、こちらは1秒間に50件処理可能だ。
よって、ネットワークの方が処理件数が少ないので、その50件が答え、つまりアが正解になる。
問16
ジョブのターンアラウンドタイムの問題だ。
先に用語を、ターンアラウンドタイムは、ジョブが到着してから、完了するまでの時間だ。
また、処理時間順方式なので、そのとき待ちになっているジョブのうち、処理時間が短いジョブが優先的に処理される。
さらに、多重度が1なので、同時に1つまでを実行することができる。
これは、処理の流れを図にした方が分かりやすいだろう。
以下に、各ジョブの到着、処理と時刻の関係を表してみる。
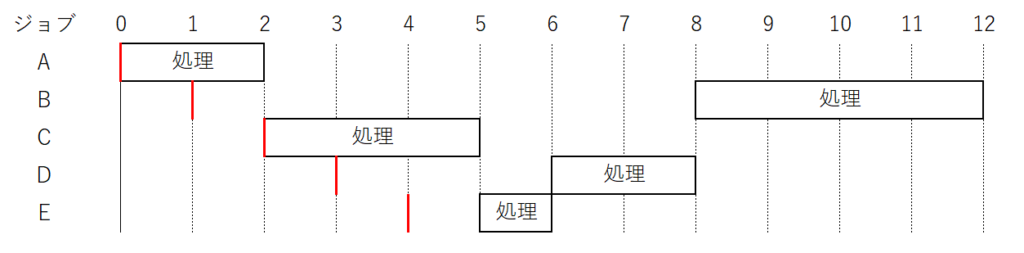
赤い線は、それぞれのジョブの到着時刻を表している。
一点だけ気を付けるべきは、2秒時点だろうか。
ここでCが到着し、BとCを比較するとCの方が処理時間が短いので、そちらが実行されている。
さて、ジョブBについて、到着時刻は1秒、完了時刻は12秒となった。
よって、ターンアラウンドタイムは12 – 1 = 11秒、エが答えになる。
問19
ページ置き換えの問題だ。
これも先に用語を一つ、LRU(Least Recently Used)は、参照されていない時間が最も長いページを置き換える方式だ。
というわけで、実際に各番地の内容を追ってみよう。
| 番地 | 1 | 2 | 3 | 4 | 2 | 5 | 3 | 1 | 6 | 5 | 4 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4000 | 1 | 5 | 5 | ||||||||
| 5000 | 2 | 2 | 6 | ||||||||
| 6000 | 3 | 3 | 4 | ||||||||
| 7000 | 4 | 1 |
ページインが発生するところを赤字にしてみた。
例えば、6番目に来ている5について、この時点ではどの番地にも5は存在しない。
そして、その直前で参照されていない期間が最も長いのは4000番地の1だ。
だから、そこが5で置き換わっている。
というわけで、最後の4がページインするのは6000番地、ウが答えになる。
問22
用語が色々並んでいるが、落ち着いて見てみよう。
まず、10kHzの周波数、16ビットで4秒間サンプリングする、とある。
求める答えがバイト単位なので、16ビットを先に2バイトに直しておこう。
周波数は1秒間の回数なので、以下の式で圧縮前の容量が得られる。
$$10k \times 2 \times 4$$
これを計算したいところだが、一旦先に進もう。
さらに、1/4に圧縮するので、上の式に1/4を掛けてあげる。
$$10k \times 2 \times 4 \times \frac{1}{4}$$
ということで、綺麗に約分ができて、答えは20kバイトとなった。
聞かれているのが何kバイトかなので、イの20が正解だ。
問23
論理回路の問題。
二つの回路の入出力表を書いてもいいのだが、入力が16パターンもありちょっと面倒なので、選択肢の状況だけ見てみよう。
まず、アについては明らかにどちらの回路も当てはまるので誤り。
同じく、エも両方当てはまる。
次に、イを見てみよう。
AとBに0、CとDに1を入力しており、B AND Cは0、ということで左側の回路のE、Fは両方とも0だ。
選択肢はE、Fともに1になっているので、これも違う。
というわけで、消去法でウが正解になる。
念のため、確認しておこう。
(A, B, C, D) = (1, 1, 0, 1)と入力していて、B AND Cは0だ。
なので、AND側の回路のEとFは0になる、ここまでは大丈夫だ。
次に、OR側の回路を見る。
B OR Cは1なので、OR側の回路のEとFは両方とも1、こちらは当てはまらない。
よって、AND回路だけ正しくなっているので、やはりウが正しい、ということになる。
問34
IPアドレス(ネットワークアドレス)の問題だ。
サブネットマスクはネットワークアドレスがどこまでかを表すもので、IPアドレスとサブネットマスクを2進数にし、各ビットでANDを取ることでネットワークアドレスが得られる。
選択肢について、第3オクテットまでは全て同じなので、第4オクテットだけ見ていこう。
まず、問題のIPアドレスの第4オクテットは19なので、2進数に直すと0001 0011だ。
次に、サブネットマスクの第4オクテット240を2進数に直すと、1111 0000となる。
このANDを取ると、0001 0000となり、10進数に戻すと16となる。
よって、ネットワークアドレスの第4オクテットは16、イが正解だ。
問52
申し訳ないが、この問題に関してはまだ私の理解が浅い。
そのため、是非ご自身でも調べて欲しい。
ここは、アーンドバリューマネジメント(以下、EVM)についての問題だ。
このEVMとは、プロジェクトの進捗などを、コスト換算で管理しよう、というもの。
先に今回必要な用語をざっと解説してしまおう。
まず、完成時総予算(以下、BAC)とは、計画段階でのプロジェクト全体でかかるコストのこと。
プロジェクトを細かいタスクに分解して、それぞれにかかるコストを予想した上で合計を求める、という形で算出する。
表より、今回のプロジェクトでは総計100万円のコストがかかる予定だと分かる。
次に、プランドバリュー(以下、PV)は、現時点で予定している総コストのこと。
現在5日目が終了した時点で、そこまでのタスクが完了しているとすると、50万円のコストがかかっている計算だ。
そして、アーンドバリュー(以下、EV)は、実際に終わったタスクに対して予想していたコストの合計だ。
表を見ると40万円となっており、今完了しているタスクで予想されていたコストの合計がこれだ。
そして、表の最後にある実コスト(以下、AC)が、実際にかかったコストだ。
表から、実際には60万円使っていると分かる。
さて、軽く状況を整理しよう。
今、全体で100万円のコストがかかると予想していたプロジェクトで、半分の5日目が終了している。
ここまで、50万円のコストが発生する分のタスクが完了している予定だった。
しかし、実際に終わっているタスクは40万円分、しかも実際のコストは60万円かかっている。
なんとなく、状況は掴めただろうか。
では、問題に戻ろう。
求める完成時コスト見積り(以下、EAC)は、現時点の状況がそのまま続いた場合に予想される総コストだ。
計算の方針としては、三段階に分かれる。
まず、現時点で完了しているタスクの予想コスト(EV)と実コスト(AC)の比を求める。
次に、上で求めた比と計画段階でのコストから、残りのタスクでかかりそうなコストを求める。
それに、現時点でかかったコストを足してあげれば、EACが求まる、ということだ。
早速計算していこう。
まず、EV : ACは40 : 60 = 2 : 3より、この時点で予定より1.5倍のコストがかかっていることになる。
残りタスクの予定コストはBAC – EVで求められ、60万円分だ。
今、1.5倍のズレがあると分かっているので、60 × 1.5 = 90万円が今からかかりそう、ということがわかる。
これに現時点での実コスト60万円を足して、150万円がこの時点でのEACだ。
というわけで、答えはエになる。
問53
作業工数の問題だ。
シンプルに、各選択肢を見ていこう。
まずアについて、Cは前提としてA、Bが終わっていなければいけない。
Bが10日かかるので、最速でも11日目からでないと始めることができず、誤りとなる。
イについて、クリティカルパスを求めてみるとB→C→G→Hとなる。
この中にDはないので、これも誤り。
ウについて、作業C、D、E、Gに注目してみると、C→Gが最長で40日かかる。
E自体は10日で終わるため、40 – 10 = 30日の余裕があり、これが正しい。
ちなみに、選択肢のエ、Fは最速で11日目、最遅で41日目に始めればいいので、誤りだ。
以上から、答えはウだ。
作業工数の問題については、一部の作業が〇日短縮できたら全体は何日短縮できるか?といった問題がよく出る印象がある。
そのため、クリティカルパスは出せるようにしておこう。
問56
バックアップに関するお話だ。
前提として、差分バックアップを行うためには、直前のフルバックアップのデータが必要なことに注意してほしい。
6か月前の同日まで戻すことを考えた場合、まず当月分のフル、差分バックアップは取っているので、2本。
1ヶ月前だと、その月のフル、差分が必要なので+2本。
2ヶ月前だと、その月のフル、差分が必要なので+2本。
という感じで、6か月前だと、今月分+6×2で計14本必要になる。
具体例でも見てみよう。
例えば、この記事を書いている10/8の場合、6か月前だと4/8まで戻せなければいけない。
ということで、10月分、9月分、8月分、…、4月分のフル、差分バックアップが必要になる。
これは7か月分あるので、結局14本、なのでウが正解になる。
ちなみに、4月分のフルバックアップがないと差分バックアップが使えなくなるので、間違えて13としないよう注意だ。
問64
問52と同じく、ここもまだ理解が浅い。
ここに書いてあることは参考程度に読み流してほしい。
この問題は、正味現在価値法という、投資効果を見極める計算だ。
考え方としては、投資によって将来得られるお金は、現在価値にするといくらになるか、というもの。
先に計算式を出してしまおう。
$$現在価値 = \frac{n年後の回収額}{(1 + 割引率)^n}$$
ちょっと具体例で見てみよう。
今、100万円を投じると、1年後に110万円になる投資がある。
割引率を5%としたとき、この1年後に戻ってくる110万円を現在価値に直すと…
$$\frac{110}{(1 + 0.05)^1} = \frac{110}{1.05} \sim 104.8$$
大体105万円くらいになる。
ということは、現在価値に直しても投資額の100万円より高いので、投資すべき、と判断できる。
こんな感じで計算していく。
さて、もう一度式を見てみよう。
$$現在価値 = \frac{n年後の回収額}{(1 + 割引率)^n}$$
これを見ると、同じ割引率の場合、年数が経てば経つほど分母が大きくなる、つまり現在価値は下がっていく。
つまり、大きい金額を先に回収できた方がお得なのだ。
選択肢を見ると、Bが大きい金額を先に回収できるので、一旦AからCの中ではBが最も効果が高いとわかる。
では、投資をしない場合とどちらがいいか、実際にBの現在価値を計算していこう。
$$\frac{120}{(1 + 0.05)^1} + \frac{80}{(1 + 0.05)^2} + \frac{40}{(1 + 0.05)^3} \sim 221.4$$
ということで、投資額の220万円より大きくなったため、Bの投資をした方が効果が高い。
よって、答えはB、イになる。
問75
…三つ目の理解が浅い問題だ。
先にまた用語を見ていこう。
まず、定量発注方式とは、在庫が発注点というラインに達したときに発注する方式のこと。
例えば、この発注点が50個だとすると、在庫が50個になった時点で発注がかかることになる。
次に、経済的発注量とは、発注費用と在庫費用の合計が最も安くなる発注量のこと。
…今回の問題では600個と言われているが、実は計算には関係ない。
安全在庫量とは、需要のブレに対応するために抱えておくべき最低ライン以上の在庫量のこと。
例えば、平均で1日50個売れる商品があったとして、用意するのがちょうど50個だと欠品の可能性が出てくる。
それを防ぐために、これくらいは余分に持っておこう、というのが安全在庫量だ。
さて、問題では発注から納品まで5日あり、1日の平均消費量が50個と言われている。
よって、在庫数が5 × 50 = 250個の時点で発注しないとまずい。
そして、安全在庫量は30個なので、250と足して280個を切った段階で発注をかけることになる。
これが発注点となり、答えはウだ。
問76
費用に関するお話、前回解説した令和元年度秋季だと損益分岐点分析が出てきていた。
が、今回は変動費率周りさえ分かっていれば解ける問題になっている。
まず、その変動費率を求めていこう。
変動費率は売上に対する変動費の割合なので、10,000 / 20,000 = 0.5となる。
これが変わらないので、計算にそのまま使える。
さて、変更後の売上を\(x\)として計算式を作っていこう。
固定費が+1,000、売上総利益を3,000にしたいので…
$$x – 0.5x – (8000 + 1000) = 3000$$
という式が出来上がる。
これを\(x\)について解くと、\(x = 24000\)となる。
さて、聞かれているのが、いくら増加させればいいか、元が20,000だ。
というわけで、増加分は4,000、ウが正解になる。



コメント