【備忘録】平成29年度秋 応用情報 午前の計算問題

過去に進むにつれて、やはり重複する問題が増えるせいか、だんだんと問題を解くスピードが速くなってきた。

知識は知っているかどうかでぱっと答えられるので、いかに計算にかける時間を減らすか、というのも一つのポイントだろう。

是非、時間を測って解くようなことにもチャレンジしてみてほしい。

さて、今回も引き続き過去にさかのぼって応用情報の計算問題を解説していく。

今回の対象は、「平成29年度 秋季 応用情報技術者試験 午前」の計算問題。

いつも通り、問題文は上のリンクから、計算問題は独断と偏見で選んだものだ。

また、気を付けてはいるが、誤りがあったら申し訳ない。

では、始めていこう。

問2

BNFの問題、過去解説した中でいくと平成30年度秋の問4にも出てきている。

一応そのリンクも貼っておいたので、気になる人は見てみよう。

さて、今回のBNFはちょっと複雑なので、生成規則だけ見て解く、というのが面倒だ。

というわけで、選択肢の文字列をBNFの非終端記号に書き換えてみよう。

まず、アから。

• 123
• <\(R_1\)><\(R_2\)><\(R_0\)>
• <B><\(R_2\)><\(R_0\)>
• <A><\(R_0\)>
• <A>

ということで、いきなり答えが出てしまったが、アが正解だ。

ちょっと、ここは丁寧に解説しておこう。

最初、1、2、3それぞれを非終端記号の<\(R_n\)>に置き換える。

次に、先頭の<\(R_1\)>について、<B>の中に<\(R_1\)>単体があるので、置き換える。

そこから、今度は<B><\(R_2\)>という塊で見ると、これは<A>に含まれるので置き換え。

もう一度、<A><\(R_0\)>も<A>に含まれるので、これで置き換えて完了だ。

ちなみに、イ以降もやってみよう。

イについて。

• 124
• <\(R_1\)><\(R_2\)><\(R_1\)>
• <B><\(R_2\)><\(R_1\)>
• <A><\(R_1\)>
• <B>

ウについて。

• 127
• <\(R_1\)><\(R_2\)><\(R_1\)>
• <B><\(R_2\)><\(R_1\)>
• <A><\(R_1\)>
• <B>

エについて。

• 128
• <\(R_1\)><\(R_2\)><\(R_2\)>
• <B><\(R_2\)><\(R_2\)>
• <A><\(R_2\)>
• <C>

こんな感じになる。

問3

ビット変換の割合計算だ。

方針は、まず変換後の1アルファベットに対する平均ビット長を求める。

そのあと、元の2ビットとの比を求めればいい。

では、その変換後の平均ビット長を求めていこう。

変換後のビットの長さに出現確率を掛け、それらを足し合わせればいい。

アルファベットaについて、ビット長は1、出現確率は40%なので掛けて0.4。

同じように、bは0.6、cは0.6、dは0.3となる。

ということで、これらを足し合わせて、変換後の平均ビット長は1.9だ。

最後に、これを変換前の2ビットで割ればいいので…

$$\frac{1.9}{2} = 0.95$$

ということで、答えはエだ。

問6

グラフ構造の隣接行列に関する問題、これは知識が必要になるだろう。

そもそも、グラフ構造とは、点の集合と、そのうち2点を結ぶ辺の集合で定義される数学的な構造だ。

それを隣接行列というもので表すとき、まず各行・列のn番目が点nに対応している。

今回、5行5列の行列なので、点の個数は5個、上からと左から1個目の点、2個目の点、…となっている。

そして、点iと点jが辺で繋がれているとき、i行j列とj行i列に1が入る。

もう一つの用語、木構造についても解説しておこう。

木構造とは、全ての点を辺を通って辿れ、かつ輪っか状になっている個所がないグラフ構造だ。

この、全ての点が辺を通して繋がっている状態を連結、輪っか状になっている部分を閉路とも呼ぶので、覚えておこう。

この用語で言い直すと、木構造とは連結かつ閉路を持たないグラフ構造、となる。

これで、各選択肢の具体的なグラフを見ていってもいいのだが…

実は、木構造の辺の個数は必ず点の個数-1になるという性質がある。

これで、まず辺が4つのものだけ見ればよいことが分かる。

今、1つの辺に対して二つの1があるので、各選択肢について1の個数を数えて2で割れば辺の個数が出てくる。

それを使って数えると、アは5本、イは4本、ウは5本、エは6本。

ということで、辺の個数が点の個数-1になっているのはイだけなので、これが正解だ。

問7

再帰関数の問題。

nの階乗を求めるfact(n)を定義したい。

n=3として、選択肢を順番に見ていこう。

まずはア。

• fact(3) = 3 × fact(2)
• fact(2) = 2 × fact(1)
• fact(1) = 1 × fact(0)
• fact(0) = 0

これでは、どんな非負整数を入れても0になってしまう。

次にイ。

• fact(3) = 3 × fact(4)
• fact(4) = 4 × fact(5)
• …

…数が増えてしまい、終わらないので不適だ。

そしてウ。

• fact(3) = 3 × fact(2)
• fact(2) = 2 × fact(1)
• fact(1) = 1 × fact(0)
• fact(0) = 1
• fact(1) = 1 × 1 = 1
• fact(2) = 2 × 1 = 2
• fact(3) = 3 × 2 = 6

というように、上手くいっている。

最後に、エも見ておこう。

• fact(3) = 3 × fact(4)
• fact(4) = 4 × fact(5)
• …

イと同様に、数が増えてしまい、終わらない。

よって、正しく計算できたのはウだ。

ちなみに、意味から考えていってもいい。

まず、n=0の時、0!=1なので、この時点でア、イは不適。

次に、n! = n × (n – 1) × … × 1 = n × (n – 1)!なので、nと(n-1)!を返せばいいことになる。

ここから、ウが正解、とも導けるのだ。

こちらの場合、具体的な数字による計算は検算として使えるだろう。

問11

これは、まったく同じ問題が令和元年度秋の問10に出ている。

解説はそちらを参照してほしい。

問14

CPU使用率の問題。

色々条件が書かれているので、落ち着いて一つずつ確認していこう。

まず、求めなければいけないのは、ピーク時間帯のCPU使用率だ。

ピーク時間帯は1時間とあるので、そのうちの何秒処理をしているかが分かれば、求めることができる。

CPU処理はトランザクションで、1日平均54,000件、ピーク時はその20%になる。

そのため、ピーク時のトランザクション数は54,000 × 0.2 = 10,800件と分かる。

さらに、トランザクションは1件あたり、100レコードへのアクセスと計算が必要。

レコードアクセスと計算それぞれにかかる時間も提示されているので、あとはひたすら計算だ。

まずレコードアクセスについて。

トランザクション1件あたり100レコードへのアクセス、1レコードへのアクセスは1ミリ秒なので、

$$10800 \times 100 \times 1 = 1080000$$

より、1080000ミリ秒かかる。

のちほど秒単位で計算したいので、先に直してしまうと1080秒だ。

次に計算時間について。

トランザクション1件あたり100ミリ秒の計算時間がかかるので、

$$10800 \times 100 = 1080000$$

レコードアクセスと同じようにミリ秒単位になっているので、秒に直して1080秒だ。

あとは、1時間=3600秒のうち、どれだけ計算しているかの割合を出せばいいので…

$$\frac{1080 + 1080}{3600} = 0.6$$

聞かれているのは%単位なので60%、エが正解になる。

問15

ジョブに関するターンアラウンドタイムの問題。

平成31年度春の問16にも似たようなものは出ていて、その時と同じ考え方で問題ない。

が、数字等違うので、改めて解説しよう。

まず、用語の確認。

ターンアラウンドタイムとは、ジョブが到着してから、そのジョブの処理が完了するまでの時間のことだ。

到着から開始するまで等ではないので気を付けよう。

さて、この手の問題は図に書けば一発で分かる。

というわけで、各ジョブの到着、処理の様子を図にしてみよう。

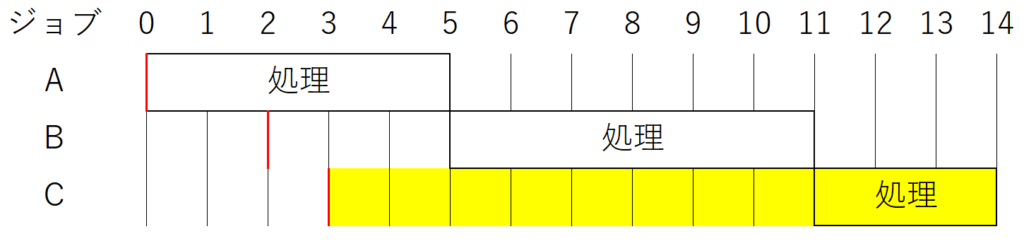
赤線が各ジョブの到着時刻、黄色が今回求めるジョブCのターンアラウンドタイムだ。

今回、多重度が1なので、同時に実行できるジョブの数は1だ。

そして、到着順に処理がされるので、優先度はAが最も高く、Cが最も低い。

よって、上の図のような動きになり、ジョブCのターンアラウンドタイムは11秒、アが答えになる。

問23

論理回路の問題、もはやこれも定番だろう。

ただ、今回は解き方が二通りある。

一つは得たい出力について真理値表を作り、それに合致した回路図を選ぶ。

一つは各選択肢の真理値表を作り、条件を満たしているものを選ぶ。

どちらで解いてもらってもいいが、前者は2つの真理値表であるのに対し、後者は最大8つの真理値表が必要になる。

そのため、前者の方が楽なため、解説も前者で行おう。

入力AとGに対する出力X、入力BとGに対する出力Yをそれぞれ真理値表で表してみる。

A	G	欲しいX
0	0	0
0	1	1
1	0	1
1	1	0

B	G	欲しいY
0	0	0
0	1	1
1	0	1
1	1	0

よって、両方とも排他的論理和の関係になっている。

これを表している回路はウだ。

なお、回路図の素子が何を表しているかは、一応問題冊子の問1前に載っている。

無くなることはないと思うが、一応覚えておいた方がいいだろう。

ちなみに、選択肢アのX手前はAND、Y手前はNAND、イは両方OR、ウは上の通り排他的論理和(XOR)、エのY側のAND手前にあるのがNOTだ。

問29

これまでの解説ではあまり見なかったタイプの問題だ。

グラフで、各トランザクションが待っている資源の関係が表されている。

これで、永久待ち状態になるトランザクションはどれか、という問題。

永久待ち状態になるには、資源を待っている先がループしていることが条件になる。

よって、まずはB, C, Dが該当する。

このとき、これら三つの処理が、互いをずっと待っている状態だ。

つまり、これらの資源を待つ処理も、またずっと待たされることになる。

ということで、B, C, Dに向かう矢印を持つのはFだけ、このFを待つ処理はないので、最終的にB, C, D, Fの4つが永久待ち状態となる。

よって、答えはウだ。

問32

応答時間の問題、基本的に通信速度の問題が分かっていれば苦労することはないだろう。

まずは、その通信にかかる時間を求めていこう。

回線速度は8Mビット/秒、データがバイト単位で表記されているので先に1Mバイト/秒に直しておく。

伝送効率が60%なので、実質の速度は0.6Mバイト/秒だ。

次に、上りのデータ量は1Mバイトなので、上りにかかる時間は、

$$\frac{1}{0.6} = \frac{5}{3}$$

小数に直してもいいが、一旦このまま進む。

下りについて、データ量は2Mバイト、同じように計算していこう。

$$\frac{2}{0.6} = \frac{10}{3}$$

ということで、通信時間はこれらの合計なので、

$$\frac{5}{3} + \frac{10}{3} = \frac{15}{3} = 5$$

綺麗に約分できて、通信だけの時間は5秒と分かった。

最後に、クライアント、サーバでの処理時間を足してあげる。

両方とも送受信を合計した数値で出してくれているので、そのまま1回分ずつ足せばいい。

$$5 + 0.4 + 0.4 = 5.8$$

ということで、答えはエの5.8秒になる。

問39

パスワードの種類数を求める計算、どちらかというと数学に近い問題だ。

今、文字の種類がMあり、それをn個組み合わせるとある。

つまり、1文字目にはMパターン、2文字目にはMパターン、…と続いていく。

同じ文字が連続してはいけない、などの条件は一切ないので、パターン数は単純にこれらを掛け合わせればいい。

よって、Mをn個掛けるので総パターン数は\(M^n\)、アが正解だ。

問53

工数の問題だが、これまで解説してきたタイプとはかなり異なる。

これまでは提示された具体的な工数から問題を解いていたが、今回はその提示されていた部分を作る問題になっている。

まず、問題で与えられているグラフは、作業を点としたグラフ構造になっている。

前提として、FS関係とあるが、これは前の作業が終了したら次の作業を開始できることを表している。

これを、矢印を作業としたグラフ構造に書き直せばいい。

見ると、作業A、作業Dから作業Fに向かって矢印が伸びている。

つまり、Fを開始するためにはこれら二つの作業を終えていることが必要だ。

これを踏まえ、各選択肢を見ていこう。

まずア、これは作業Aが終わっていなくても作業Fに入れてしまうので不適。

次にイ、特に問題がなく、イが正解となる。

念のためウとエについても見てみよう。

ウについて、この形にするには、元の図で作業Aから作業Hに向かう矢印も必要になるので不適。

エについて、アと同じく作業Aが完了していなくても作業Fを開始できてしまうので不適だ。

問55

可用性の割合を求める問題。

まず、可用性を求めるためには、本来稼働しているべき時間と、実際にその中で稼働した時間が分かればいい。

それらが分かれば、稼働した時間を稼働すべき時間で割れば、可用性が出てくる。

というわけで、まずは本来稼働しているべき時間を求めていく。

毎日6時～20時までなので1日は14時間、それが30日あるので、月420時間が稼働すべき時間だ。

それに対し、サービス提供時間内で止まったのは、条件aの7時間だけ。

条件b、cはサービス提供時間外での停止なので、今回の可用性には影響しない。

よって、最終的な計算式は以下の通り。

$$\frac{420 – 7}{420} =0.98333… \sim 0.983$$

以上から、答えは98.3%、ウが正解になる。

問70

部品の計算問題。

まず、製品A1個作るのに必要な部品bの個数を求めていこう。

製品A1個に対し、部品aは3個、bは2個必要。

その部品a1個を作るために、部品bが1個、部品cが2個必要だ。

ここから、製品A1個に対し、部品bは2 + 3 × 1 = 5個必要とわかる。

さて、今製品Aを300個出荷したい。

製品Aは元々100個の在庫があるので、残り200個を作る必要がある。

必要な部品bの総数は1000個だ。

ここで、部品aが100個の在庫ありで、そのために必要だった部品bの個数は100個、より必要な個数は100個減る。

さらに、部品b自体も300個あるので、1000 – 100 – 300 = 600個これから必要になる。

ということで、答えはイだ。

問75

なぜ応用情報の問題なのだろうか、とちょっと思ってしまったくらい数学のお話。

確率の絡む平均が分かっていれば問題なく解けるだろう。

さて、ここで4つの状態に場合分けしてみる。

• パターン1：高速道路が混んでいて、なおかつ交通情報も渋滞と出る場合
• パターン2：高速道路は混んでいるが、交通情報は順調と出る場合
• パターン3：高速道路は空いているが、交通情報は渋滞と出る場合
• パターン4：高速道路が空いており、なおかつ交通情報も順調と出る場合

このそれぞれになる確率を先に求めてしまおう。

まずパターン1、実際に混雑している場合に、渋滞と出る確率は表から0.9と分かる。

これに道路が混雑する確率を掛ければいいので、0.9 × 0.4 = 0.36となる。

同様に、パターン2は0.1 × 0.4 = 0.04だ。

パターン3、道路が混雑していない確率は0.6なので、0.2 × 0.6 = 0.12。

最後、パターン4は0.8 × 0.6 = 0.48。

ちょっと計算が多いので、一旦ここでまとめておこう。

なお、それぞれのパターンで実際にかかる時間も表に入れてみる。

パターン	確率	かかる時間(分)
1	0.36	80
2	0.04	100
3	0.12	80
4	0.48	50

あとは、単純に平均値を求めればいい。

各パターンにおける確率と所要時間を掛け、それらの合計を出せば求まる。

これを計算すると、66.4分となり、およそ66分なので選択肢のイが正解となる。

問77

論理回路と並び定番の損益分岐点分析だ。

今回は、今年度の情報が与えられており、変動費率が変わらない場合に次年度を計算する。

過去私が書いた解説を見てくださっている方にはもうくどいかもしれないが、やはり復習はしておこう。

変動費率とは売上全体に対する変動費の割合で、以下の式で求められる。

$$変動費率 = \frac{変動費}{売上}$$

どんなに簡単な問題でも、この式は毎年必ず使うので覚えておこう。

さて、今年の情報をちょっとまとめて、改めて表に直しておこう。

項目	金額(単位：百万円)
売上高	1,600
変動費	960
固定費	480
利益	160

来年度について、今年度と変動費率が変わらず、固定費を追加して利益を240百万円にしたい。

そのとき、来年度の売上高をいくらにすればいいか聞かれているので、それを\(x\)にする。

今\(x\)が入っているが、その状態で来年の目標を表にしてみよう。

項目	金額(単位：百万円)
売上高	\(x\)
変動費	\(0.6x\)
固定費	480 + 80 + 20 = 580
利益	240

ということで、あとはひたすら計算になる。

売上高から変動費、固定費を引けば利益になるので、以下の式が立てられる。

$$x – 0.6x – 580 = 240$$

これを解くと\(x = 2050\)、よって選択肢のエが正解だ。