本シリーズでは、以下の本に沿って数学を解説している。
前回は、微分の基本を解説した。
微分とは導関数を求めること、導関数はある点における接線の傾きを求めることだ、ということを説明してきた。
また、幾つか導関数をカンタンに求める公式と、微分の線形性についても解説した。
今回の内容に繋がってくる部分もあるので、しっかりと確認しておこう。
以下がその記事だ。
今回は、微分の続きということで、合成関数の微分、関数の最小値について解説していこう。
本当は多変数関数の微分も書きたかったのだが、ちょっと長くなってしまうのでもう一つ区切ることにする。
微分の記号
さて、いきなりだがちょっと横道に逸れたい。
前回の記事で、関数\(f(x)\)を微分して求める導関数は\(f'(x)\)と表記すると説明した。
のだが、実はもう一つ表記方法がある。
関数\(f(x)\)を改めて\(y\)と置いて、これについて導関数\(f'(x)\)は以下のようにも表記できる。
$$f'(x) = \frac{dy}{dx}$$
この意味は、\(y\)を\(x\)で微分している、というものだ。
なぜこれを紹介したかというと、次回解説する多変数関数の微分時に便利だからだ。
元々のプライムだけをつけた導関数の記号では、どの変数に関する微分なのかが分からない。
もうちょっと言い換えると、極限を取っていた\(\Delta x\)が、どの変数に対してのものなのかが分からないのだ。
それに対し、今回の分数のような表記にすると、どの変数で微分しているか、というのが明確になる。
これがあるおかげで非常に分かりやすくなるので、今後は慣れるためにも使える場合はこちらを使っていこう。
また、もう一つメリットがあるのだが…それは解説しながら紹介することとしよう。
合成関数の微分
ようやく本編開始だ。
まずは、合成関数の微分について。
…なのだが、その前にそもそも合成関数とは何ぞやという疑問があると思う。
なので、合成関数から解説をしていこう。
合成関数
合成関数とは、ある関数の変数部分が、さらに別の関数になっているようなもののことだ。
記号で書き直してみる。
ある関数\(y = f(u)\)があり、その変数\(u\)もまた別の関数\(g(x)\)となっているとき、\(y\)は以下のように書き表すことができる。
$$y = f(g(x))$$
このように、関数が入れ子構造になっている状態のとき、この\(y\)を\(f(u)\)と\(g(x)\)の合成関数と呼ぶのだ。
幾つか、具体的な合成関数の例を見てみよう。
例えば、\(y = (x – 1)^2\)。
これはカンタンに展開できるのでありがたみは薄いが、\(u = g(x) = x – 1\)と見なせば…
$$f(u) = u^2$$
と書き直すことができる。
よって、\(f(u) = u^2\)、\(u = g(x) = x – 1\)の合成関数と見なすことができるのだ。
もう一つ、今度は指数関数で出してみよう。
\(y = e^{3x + 2}\)という関数を見てみる。
今度は、\(u = g(x) = 3x + 2\)とすれば、\(f(u) = e^u\)と単純にできる。
このように、ある関数の中に隠れる別の関数を見つけ出すのがポイントになる。
合成関数の微分公式
さて、上で解説したような合成関数を微分したいとしよう。
式変形をして公式を使ったり、最悪導関数の定義を使えばゴリゴリ計算でも求めることはできるだろうが、さすがに骨が折れるだろう。
ということで、もちろん便利な公式が用意されている。
ある関数\(y = f(u)\)があり、さらに\(u = g(x)\)と表されているとする。
このとき、\(y\)を\(x\)で微分するとき、以下のように行うことができる。
$$\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}$$
言葉で説明すると、合成関数\(y\)を\(x\)で微分するとき、まず\(y\)を\(u\)で微分し、それとは別で\(u\)を\(x\)で微分したものと掛けて求められる。
…言葉で説明しても分かりづらいと思うので、具体例で見ていこう。
上の合成関数の例で出した、\(y = (x – 1)^2\)を微分してみる。
先に、答えが合っているか確認するために、普通に展開して微分してみよう。
$$y = x^2 – 2x + 1$$
$$\frac{dy}{dx} = 2x – 2$$
ここまでは前回の復習で大丈夫だと思う。
では、今度は合成関数として微分してみよう。
今回、\(y = u^2\)、\(u = x – 1\)という形の合成関数になっているので、まずはそれぞれで微分してみる。
$$\frac{dy}{du} = 2u$$
$$\frac{du}{dx} = 1$$
こんな感じだ。
では、公式通り、これらを掛け合わせよう。
$$\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} = 2u \cdot 1 = 2u$$
最後に、\(u = x – 1\)だったので、代入して…
$$\frac{dy}{dx} = 2(x – 1) = 2x – 2$$
ということで、同じ答えが出てきた。
さて、もう一度公式を見てみよう。
$$\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}$$
この右辺について、微分の記号を単に文字として見てみると、綺麗に約分できて左辺と同じ形になる。
このように、今回説明した記号を使うと、微分の計算がまるで分数のように解釈できるので、とても便利なのだ。
これが、もう一つのメリットだ。
合成関数の微分公式から求められる公式
さて、合成関数の微分を知っていると、さらに別の公式も導くことができる。
何かというと、分数の形をしている関数の微分だ。
ある関数\(y\)が、以下のような形になっていたとしよう。
$$y = \frac{1}{f(x)}$$
このとき、\(y\)の導関数は以下のようになる。
$$\frac{dy}{dx} = -\frac{f'(x)}{\{f(x)\}^2}$$
これをさくっと証明してみよう。
まず、合成関数として、\(y = \frac{1}{u}\)、\(u = f(x)\)と置く。
これで、\(y\)を\(u\)で微分しよう。
分数は、指数を使って以下のように書き直せる。
$$\frac{1}{u} = u^{-1}$$
これで前回の微分公式を使うと…
$$\frac{dy}{du} = -1 \times u^{-2} = -\frac{1}{u^2}$$
そして、\(u\)を\(x\)で微分したものと掛け合わせ…
$$\frac{dy}{du} \frac{du}{dx} = -\frac{1}{u^2} \times f'(x)$$
両辺整理して…
$$\frac{dy}{dx} = -\frac{f'(x)}{\{f(x)\}^2}$$
ということで、公式が得られた。
これが分かると、例えば関数のところで紹介したジグモイド関数の微分も公式を作ることができる。
ジグモイド関数を再掲しよう。
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
まずは、合成関数として書き直してみよう。
\(f(x) = 1 + e^{-x}\)として、以下のように書き直せる。
$$\sigma(x) = \frac{1}{f(x)}$$
そのまま、分数の微分が使えるので、導関数は以下の通りだ。
$$\sigma'(x) = -\frac{f'(x)}{\{f(x)\}^2}$$
ここで、\(f'(x)\)を求めよう。
\(u = g(x) = -x\)として、合成関数の微分を使う。
$$\frac{d}{du}(1 + e^u) = e^u$$
$$\frac{d}{dx}(-x) = -1$$
これらを掛け合わせて…
$$f'(x) = -e^{-x}$$
となる。
これを、元の式に代入しよう。
$$\sigma'(x) = \frac{e^{-x}}{(1 + e^{-x})^2}$$
これで一応求まったのだが、まだ形が複雑なのでもうちょっと式変形を続けよう。
まず、分母の2乗を分解して、以下のように書き直す。
$$\sigma'(x) = \frac{1}{1 + e^{-x}} \times \frac{e^{-x}}{1 + e^{-x}}$$
右辺の左側がそのままジグモイド関数になっているので、記号で置き直そう。
$$\sigma'(x) = \sigma(x) \times \frac{e^{-x}}{1 + e^{-x}}$$
ちょっと綺麗になったが、右辺の右側もなんとかしたい。
そこで、その部分だけに注目して、以下のように変形してみよう。
$$\frac{e^{-x}}{1 + e^{-x}} = \frac{1 + e^{-x}}{1 + e^{-x}} – \frac{1}{1 + e^{-x}}$$
すると、さらにジグモイド関数の形が出てきた。
これも置き直してみよう。
$$\frac{e^{-x}}{1 + e^{-x}} = 1 – \sigma(x)$$
これを、元の場所に置き直す。
$$\sigma'(x) = \sigma(x) (1 – \sigma(x))$$
これで綺麗になった。
ということで、ジグモイド関数の微分はわざわざ導関数を求めなくても、ただの計算で求めることができる。
これは、後で解説する勾配降下法という手法で用いることになる。
しっかり覚えておこう。
関数の最小値の条件
前回、導関数はある\(x\)におけるグラフ上の傾きを表していると説明したと思う。
それを利用した原理があるので、紹介しておこう。
ある関数\(f(x)\)が\(x = a\)で最小となるとき、\(f'(a) = 0\)である、というものだ。
これは、意味を考えると分かりやすい。
関数が\(x = a\)で最小値となるということは、その少し前では減少していっており、その少し後では増加していっている。
つまり、必ず傾きも前後でマイナスからプラスになっている。
このとき、傾きは一気に飛ぶことはないので、必ず0になる瞬間がある。
そこが、最小となるのだ。
ただ、これは注意が必要な原理でもある。
上で主張しているのは、あくまで「最小値となる部分の接線の傾きがゼロ」というだけで、「接線の傾きがゼロなら最小値」ではない。
具体例として、以下の関数の最小値を求めてみよう。
$$f(x) = 3x^4 – 4x^3 – 12x^2 + 32$$
先にグラフを出すと以下のようになっている。
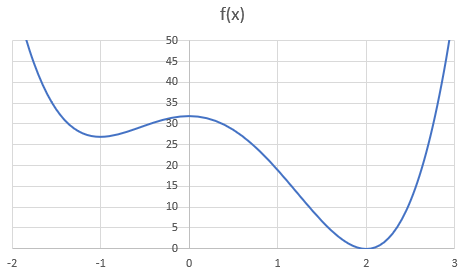
では、この最小値を求めてみよう。
上の原理から、この導関数の値が0となるところを調べればいい。
ということで、まずはその導関数を求めてみよう。
$$f'(x) = 12x^3 – 12x^2 – 24x$$
この\(x\)がいくつの時に\(f'(x)\)がゼロかを見たいので、因数分解をしてみよう。
$$f'(x) = 12x(x^2 – x – 2) = 12x(x + 1)(x – 2)$$
ということで、\(x = 2, 0, -1\)のときに\(f'(x) = 0\)となることが分かった。
ここから、高校の時にやった増減表を書いてみよう。
| x | … | -1 | … | 0 | … | 2 | … |
|---|---|---|---|---|---|---|---|
| f'(x) | – | 0 | + | 0 | – | 0 | + |
| f(x) | ↘ | ① | ↗ | ② | ↘ | ③ | ↗ |
グラフの形とも合っている。
では、最後に①~③の値を求めていこう。
ちなみに、今回求めたいのは最小値であり、②は極大なので本来は求める必要はない。
元の関数にそれぞれの値を代入しれあげればいいだけなので、①は27、②は32、③は0。
\(x\)が-1より小さい、あるいは2より大きいときはそれぞれ\(f(x)\)は大きくなっていくので、最小値は③、つまり\(x = 2\)のときの0ということが分かった。
このように、原理と増減表を組み合わせれば最小値を求めることができる。
また、①、②は最小値ではないが導関数の値がゼロになっているので、逆が成り立たないということも分かってもらえたと思う。
おわりに
今回は、合成関数の微分と関数の最小値に関する原理を紹介した。
このあたりは高校の内容でもやっていたので、復習という人も多いだろう。
しかし、次回扱う多変数関数の微分は大学でやるような内容になる。
これまで以上に複雑な内容になるので、落ち着いて進めていこう。
2020/11/04追記
多変数関数の微分に関する記事を公開した。
2変数をメインに解説しているが、3変数以上でも同じ考え方が使える。
使用時には随時解説を入れていくので、せめて2変数の感覚だけでも掴んでおこう。



コメント