本シリーズでは、以下の本に沿って解説を書いている。

前回は新しい単元に進んで、非決定性有限オートマトンというものを定義した。
前々回までの決定性有限オートマトンとは異なり、同じ記号による遷移先が複数になったり、空集合になったりしてもいいようなものだ。
列による状態遷移がイマイチ分かりづらいかもしれないが、まずは直感的な説明で理解できれば十分だろう。
以下がその記事だ。
さて、今回は以前扱っていた決定性有限オートマトンと、前回紹介した非決定性有限オートマトンの関係について説明していこう。
その証明の中で、これらの書き換え…厳密には、非決定性有限オートマトンを決定性有限オートマトンに変換する方法も紹介する。
それと、決定性有限オートマトンの時は簡単だった、言語の補集合を認識する有限オートマトンについても考えてみる。
これは、直感的に成り立ちそうなことが実は成り立たなかったりするので、注意しておいてほしい。
決定性有限オートマトン、非決定性有限オートマトンの関係
まずはこれから見ていこう。
実は、以下のような定理がある。
ある言語\(L\)を認識する非決定有限オートマトンが存在することと、同じ言語\(L\)を認識する決定性有限オートマトンが存在することは同値である。
何を言っているかというと、決定性、非決定性はそれぞれ書き換えが可能だ、ということ。
もっと言うと、これらで認識できる言語に差がないことを表している。
これを証明していこう。
決定性⇒非決定性
まずは、決定性を前提として、非決定性が存在することを示す。
…と書いたが、これは示すほどのことでもない。
決定性有限オートマトンというのは、実は非決定性有限オートマトンの特別なパターンだからだ。
どういうことかというと、非決定性有限オートマトンの状態遷移関数\(\delta\)について考える。
任意の状態\(s \in K\)、任意の記号\(a \in \Sigma\)による遷移先\(\delta(s, a)\)は、定義によると任意の状態の部分集合いずれかだった。
その要素数が常に1だった場合…つまり\(|\delta(s, a)| = 1\)であれば、それは決定性有限オートマトンなのだ。
これが言っていることは、必ず全ての状態から、全ての記号による遷移先がただ一つ存在する、ということ。
それが決定性有限オートマトンの定義だったので、これはいいと思う。
つまり、決定性有限オートマトンが存在した時点で、それ自身が非決定性有限オートマトンでもあるので、こちらは自明なのだ。
非決定性⇒決定性
問題になるのはこちら。
ある言語\(L\)を認識する非決定性有限オートマトン\(M_N\)が存在したとしよう。
このとき、同じ言語\(L\)を認識する決定性有限オートマトン\(M_D\)も存在する。
添え字の\(N\)、\(D\)については、非決定性有限オートマトンをnfa、決定性有限オートマトンをdfaと略すことが多いので、それぞれの先頭を持ってきてつけた。
さて、この方針なのだが、まずは\(M_N\)を\(M_D\)に変換しよう。
そして、それらが同じ言語を認識することを示せればOKだ。
非決定性から決定性への変換方法
では、この変換方法を紹介する。
変換元の非決定性有限オートマトンを、\(M_N = (K, \Sigma, \delta_N, s_0, F_N)\)としよう。
このとき、変換先となる決定性有限オートマトンを\(M_D = (2^K, \Sigma, \delta_D, \{s_0\}, F_D)\)とする。
状態は前回出したべき集合になり、入力記号の集合はそのまま。
一つ注意として、決定性側の一つの状態は、非決定性側の状態の集合になっている。
例えば、\(\{s_0, s_1\}\)や\(\phi\)という状態が出てくることもあるので、これまでの感覚とちょっとずれるが、混乱しないよう気を付けよう。
初期状態も\(\{s_0\}\)で、ここまでは大丈夫。
問題となるのは、状態遷移関数\(\delta_D\)と受理状態の集合\(F_D\)をどう定義するか。
状態遷移関数から見ていこう。
\(M_D\)内の任意の状態\(s_D \in 2^K\)と任意の記号\(a \in \Sigma\)について、状態遷移関数\(\delta_D\)を以下のように定義する。
$$\delta_D(s_D, a) = \bigcup_{s_N \in s_D}\delta_N(s_N, a)$$
状態\(s_D\)は、上でも書いた通り、\(K\)の部分集合になっている。
その要素一つひとつから、\(M_N\)側において記号\(a\)で遷移することのできる全ての状態を一つの集合に和集合でまとめ、それを遷移先と定義している。
具体例は後で出すのでいったん置いておいて、先にこれが決定性有限オートマトンの定義に沿っているかを確認しよう。
決定性有限オートマトンの状態遷移関数は、状態と記号の組から、状態に向かう関数だ。
今回、状態が\(2^K\)なので、左辺は定義通りになっている。
あとは、右辺が\(2^K\)の要素、言い換えると\(K\)の部分集合になっていれば問題ない。
右辺を見ると、\(s_N \in s_D \in 2^K\)で、まず\(s_N \in K\)となる。
そして、それが状態遷移関数\(\delta_N\)に渡されており、この\(\delta_N(s_N, a)\)は非決定性有限オートマトンの定義から\(2^K\)の要素、言い換えると\(K\)の部分集合。
つまり、右辺は\(K\)の部分集合の和集合なので、結局全て計算した後も\(K\)の部分集合になる。
よって、示したいことが言えたので、この状態遷移関数\(\delta_D\)は決定性有限オートマトンの定義に沿っている。
最後、受理状態の集合\(F_D\)の定義だ。
$$F_D = \{s_D \in 2^K | s_D \cap F_N \not = \phi\}$$
一つでも\(M_N\)側で受理状態になっているような状態を要素に持てば、それ自体を受理状態にする、ということ。
明らかに状態の集合\(2^K\)の要素なので、決定性有限オートマトンの定義に沿っていることは問題ないだろう。
では、具体例で実際に変換の様子を見てみよう。
前回出した非決定性有限オートマトンの例を\(M_N\)とする。
状態遷移図を再掲しよう。
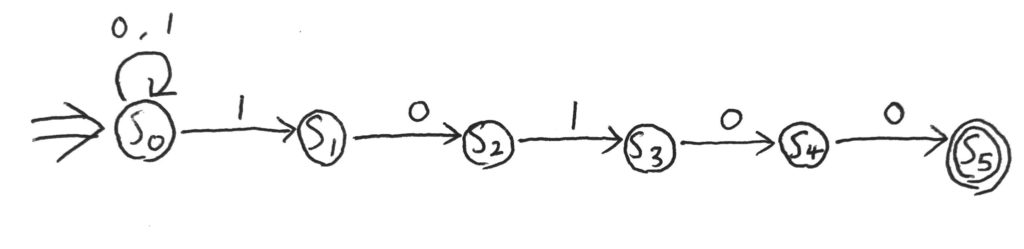
…全部考えようとすると\(M_D\)の状態数が64個ととんでもないことになるが、今回の場合は到達できるものだけに注目すれば最終的には\(M_N\)と同じ状態数になるので、このまま進もう。
さて、定義から\(M_D\)の初期状態は\(\{s_0\}\)だ。
ここから、順番に上で定義した形で状態遷移関数\(\delta_D(s_D, a)\)を決めていこう。
状態遷移関数の定義を再掲しておく。
$$\delta_D(s_D, a) = \bigcup_{s_N \in s_D}\delta_N(s_N, a)$$
まず、\(\delta_D(\{s_0\}, 0) = \delta_N(s_0, 0) = \{s_0\}\)なので、ここは自身へ遷移する。
次に、\(\delta_D(\{s_0\}, 1) = \delta_N(s_0, 1) = \{s_0, s_1\}\)、ここは別の状態へ遷移だ。
新しい状態\(\{s_0, s_1\}\)が出てきたので、これについて見ていこう。
$$\begin{eqnarray}
\delta_D(\{s_0, s_1\}, 0) & = & \bigcup_{s_N \in \{s_0, s_1\}}\delta_N(s_N, 0) \\
& = & \delta_N(s_0, 0) \cup \delta_N(s_1, 0) \\
& = & \{s_0\} \cup \{s_2\} \\
& = & \{s_0, s_2\}
\end{eqnarray}$$
$$\begin{eqnarray}
\delta_D(\{s_0, s_1\}, 1) & = & \bigcup_{s_N \in \{s_0, s_1\}}\delta_N(s_N, 1) \\
& = & \delta_N(s_0, 1) \cup \delta_N(s_1, 1) \\
& = & \{s_0, s_1\} \cup \phi \\
& = & \{s_0, s_1\}
\end{eqnarray}$$
先に言ってしまうと、これを新しい状態が出なくなるまで続ける。
これをやった結果…で結論を出してしまってもいいのだが、それだと味気ないと思うので全部やってみよう。
さて、また新しい状態\(\{s_0, s_2\}\)が出てきたので、これからの遷移を考える。
$$\begin{eqnarray}
\delta_D(\{s_0, s_2\}, 0) & = & \bigcup_{s_N \in \{s_0, s_2\}}\delta_N(s_N, 0) \\
& = & \delta_N(s_0, 0) \cup \delta_N(s_2, 0) \\
& = & \{s_0\} \cup \phi \\
& = & \{s_0\}
\end{eqnarray}$$
$$\begin{eqnarray}
\delta_D(\{s_0, s_2\}, 1) & = & \bigcup_{s_N \in \{s_0, s_2\}}\delta_N(s_N, 1) \\
& = & \delta_N(s_0, 1) \cup \delta_N(s_2, 1) \\
& = & \{s_0, s_1\} \cup \{s_3\} \\
& = & \{s_0, s_1, s_3\}
\end{eqnarray}$$
\(\{s_0, s_1, s_3\}\)は新しい状態だ。
$$\begin{eqnarray}
\delta_D(\{s_0, s_1, s_3\}, 0) & = & \bigcup_{s_N \in \{s_0, s_1, s_3\}}\delta_N(s_N, 0) \\
& = & \delta_N(s_0, 0) \cup \delta_N(s_1, 0) \cup \delta_N(s_3, 0) \\
& = & \{s_0\} \cup \{s_2\} \cup \{s_4\} \\
& = & \{s_0, s_2, s_4\}
\end{eqnarray}$$
$$\begin{eqnarray}
\delta_D(\{s_0, s_1, s_3\}, 1) & = & \bigcup_{s_N \in \{s_0, s_1, s_3\}}\delta_N(s_N, 1) \\
& = & \delta_N(s_0, 1) \cup \delta_N(s_1, 1) \cup \delta_N(s_3, 1) \\
& = & \{s_0, s_1\} \cup \phi \cup \phi \\
& = & \{s_0, s_1\}
\end{eqnarray}$$
\(\{s_0, s_2, s_4\}\)が新しい状態。
$$\begin{eqnarray}
\delta_D(\{s_0, s_2, s_4\}, 0) & = & \bigcup_{s_N \in \{s_0, s_2, s_4\}}\delta_N(s_N, 0) \\
& = & \delta_N(s_0, 0) \cup \delta_N(s_2, 0) \cup \delta_N(s_4, 0) \\
& = & \{s_0\} \cup \phi \cup \{s_5\} \\
& = & \{s_0, s_5\}
\end{eqnarray}$$
$$\begin{eqnarray}
\delta_D(\{s_0, s_2, s_4\}, 1) & = & \bigcup_{s_N \in \{s_0, s_2, s_4\}}\delta_N(s_N, 1) \\
& = & \delta_N(s_0, 1) \cup \delta_N(s_2, 1) \cup \delta_N(s_4, 1) \\
& = & \{s_0, s_1\} \cup \{s_3\} \cup \phi \\
& = & \{s_0, s_1, s_3\}
\end{eqnarray}$$
\(\{s_0, s_5\}\)が新たな状態。
$$\begin{eqnarray}
\delta_D(\{s_0, s_5\}, 0) & = & \bigcup_{s_N \in \{s_0, s_5\}}\delta_N(s_N, 0) \\
& = & \delta_N(s_0, 0) \cup \delta_N(s_5, 0) \\
& = & \{s_0\} \cup \phi \\
& = & \{s_0\}
\end{eqnarray}$$
$$\begin{eqnarray}
\delta_D(\{s_0, s_5\}, 1) & = & \bigcup_{s_N \in \{s_0, s_5\}}\delta_N(s_N, 1) \\
& = & \delta_N(s_0, 1) \cup \delta_N(s_5, 1) \\
& = & \{s_0, s_1\} \cup \phi \\
& = & \{s_0, s_1\}
\end{eqnarray}$$
これで、ようやく新たな状態が出なくなった。
全部の式変形の様子も書いてしまったので、非常に長くなってしまった。
状態遷移の様子を表でまとめよう。
| 現状態\(s_D\) | 入力記号\(a\) | 次状態\(\delta_D(s_D, a)\) |
|---|---|---|
| \(\{s_0\}\) | 0 | \(\{s_0\}\) |
| \(\{s_0\}\) | 1 | \(\{s_0, s_1\}\) |
| \(\{s_0, s_1\}\) | 0 | \(\{s_0, s_2\}\) |
| \(\{s_0, s_1\}\) | 1 | \(\{s_0, s_1\}\) |
| \(\{s_0, s_2\}\) | 0 | \(\{s_0\}\) |
| \(\{s_0, s_2\}\) | 1 | \(\{s_0, s_1, s_3\}\) |
| \(\{s_0, s_1, s_3\}\) | 0 | \(\{s_0, s_2, s_4\}\) |
| \(\{s_0, s_1, s_3\}\) | 1 | \(\{s_0, s_1\}\) |
| \(\{s_0, s_2, s_4\}\) | 0 | \(\{s_0, s_5\}\) |
| \(\{s_0, s_2, s_4\}\) | 1 | \(\{s_0, s_1, s_3\}\) |
| \(\{s_0, s_5\}\) | 0 | \(\{s_0\}\) |
| \(\{s_0, s_5\}\) | 1 | \(\{s_0, s_1\}\) |
これ以外の\(K\)の部分集合については、明らかに初期状態から到達することはできない。
そのため、そちらを考えるのは無駄なのでこれで十分だ。
では、受理状態\(F_D\)がどうなっているかを見てみる。
今、\(F_N = \{s_5\}\)なので、\(M_D\)側では各状態の要素に\(s_5\)が入っていればそれが受理状態になる。
該当するのは一つだけ、\(F_D = \{\{s_0, s_5\}\}\)だ。
以上の内容をもとに状態遷移図を書くと、以下のようになる。
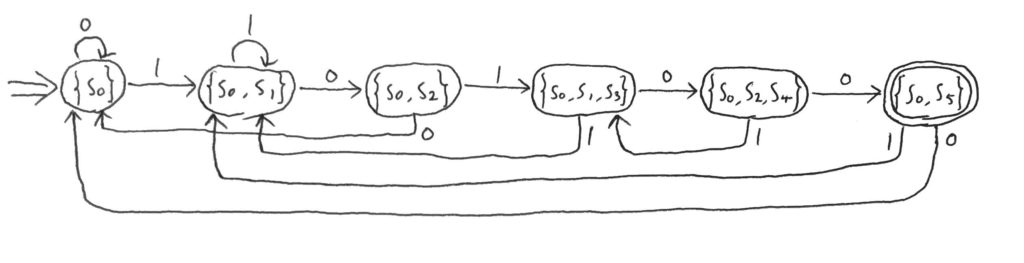
上の式で何をしていたか、分かっただろうか。
これで、とりあえず変換して決定性有限オートマトン\(M_D\)が作れた。
ここで出していた具体例はあくまで変換の具体例なので、ここからは一般的な話に戻ろう。
同じ言語を認識することの証明
…さて、最後に一つ証明しなければいけないことが残っている。
\(L(M_N) = L(M_D)\)だろうか、という点だ。
これは集合のイコールなので、任意の列\(x \in \Sigma^*\)に対し、以下が成り立っていることを示せばいい。
$$x \in L(M_N) \Leftrightarrow x \in L(M_D)$$
…これまでだと、状態遷移関数を列でも成り立つよう拡張し、そこから証明していた。
しかし、それをやろうとしたらめちゃくちゃ式が複雑になってしまった。
そのため、証明する方針を変えよう。
これらの有限オートマトンについて、任意の列\(x \in \Sigma^*\)を考える。
そのとき、以下が成立する。
$$\hat{\delta}_D(\{s_0\}, x) = \hat{\delta}_N(s_0, x)$$
…とりあえず、今回は初期状態からの列による遷移があればいいので、そこだけ考えたというわけだ。
では、列\(x\)の長さに関する帰納法でこれを示していこう。
まず、\(|x| = 0\)…\(x = \varepsilon\)について。
これは明らかに両辺とも\(\{s_0\}\)なのでいいだろう。
次に、列\(x\)で成り立っていると仮定する。
$$\hat{\delta}_D(\{s_0\}, x) = \hat{\delta}_N(s_0, x)$$
この前提の元、任意の記号\(a \in \Sigma\)を\(x\)の後ろに足して、列\(xa\)で以下の式が成り立つかを見てみる。
$$\hat{\delta}_D(\{s_0\}, xa) = \hat{\delta}_N(s_0, xa)$$
まず、左辺を決定性有限オートマトンの列の遷移の定義で書き換える。
$$\hat{\delta}_D(\{s_0\}, xa) = \delta_D(\hat{\delta}_D(\{s_0\}, x), a)$$
上で定義した\(M_D\)の状態遷移の定義から、以下のように書き換えができる。
$$\delta_D(\hat{\delta}_D(\{s_0\}, x), a) = \bigcup_{s_N \in \hat{\delta}_D(\{s_0\}, x)}\delta_N(s_N, a)$$
一旦ここで止めておこう。
次に、示したい内容の右辺を変形していく。
非決定性有限オートマトンの列による状態遷移の定義から、以下の変形が可能だ。
$$\hat{\delta}_N(s_0, xa) = \bigcup_{s_N \in \hat{\delta}_N(s_0, x)}\delta_N(s_N, a)$$
帰納法の仮定から、\(\hat{\delta}_D(\{s_0\}, x) = \hat{\delta}_N(s_0, x)\)が分かっているので…
$$\bigcup_{s_N \in \hat{\delta}_N(s_0, x)}\delta_N(s_N, a) = \bigcup_{s_N \in \hat{\delta}_D(\{s_0\}, x)}\delta_N(s_N, a)$$
両辺それぞれから出発して、同じ形に変形することができた。
よって、左辺=右辺が示せたので、これで\(\hat{\delta}_D(\{s_0\}, x) = \hat{\delta}_N(s_0, x)\)が使えるようになった。
では、ようやく本題の証明を。
左から出発して、右に同値関係を結んでいく。
非決定性有限オートマトンの列を受理することの定義から、以下が成り立つ。
$$x \in L(M_N) \Leftrightarrow \hat{\delta}_N(s_0, x) \cap F_N \not = \phi$$
今示した内容で右側を書き換える。
$$x \in L(M_N) \Leftrightarrow \hat{\delta}_D(\{s_0\}, x) \cap F_N \not = \phi$$
ここで、\(F_D\)の定義を再掲しよう。
$$F_D = \{s_D \in 2^K | s_D \cap F_N \not = \phi\}$$
これらから、明らかに以下が言える。
$$\hat{\delta}_D(\{s_0\}, x) \cap F_N \not = \phi \Leftrightarrow \hat{\delta}_D(\{s_0\}, x) \in F_D$$
決定性有限オートマトンの受理することの定義から…
$$\hat{\delta}_D(\{s_0\}, x) \in F_D \Leftrightarrow x \in L(M_D)$$
よって、成立だ。
以上から、今回考えていた\(M_D\)は、元にした\(M_N\)と同じ言語を認識する決定性有限オートマトンだ。
非常に長くなってしまったが、これで決定性、非決定性それぞれで認識できる言語に差がないことが示せた。
…証明の流れが分からなくても、とりあえず決定性・非決定性いずれかで書き表せる言語は他方でも書けるんだなぁ程度の認識はしておいてほしい。
言語の補集合を認識する非決定性有限オートマトン
本記事の最後に、これを見ていこう。
ある非決定性有限オートマトン\(M\)で認識する言語は\(L(M)\)だ。
さて、ではこの補集合\(\Sigma^* – L(M)\)を認識する非決定性有限オートマトンはどのように求めればいいのだろうか。
直感的には、決定性の時のように受理状態かどうかを入れ替えれば作れる…と思うのだが、それでは上手くいかない。
例えば、これまでも出していた以下の状態遷移図を見てみる。

これで受理状態・非受理状態を入れ替えると、なんと\(\Sigma^*\)を認識してしまう。
今、どんな列\(x \in \Sigma^*\)を入れたとしても、\(s_0\)には絶対遷移するパターンが存在する。
遷移先に受理状態が常に含まれているので、非決定性有限オートマトンが受理する列の定義から、どんな列も受理してしまうのだ。
これでは今回欲しい非決定性有限オートマトンは作れない。
ではどうするかというと、先にひと手間加える。
上の証明内で使ったような決定性有限オートマトンへの変換を行ってから、その受理・非受理を入れ替えてあげるのだ。
先の説明の通り、決定性有限オートマトンは非決定性有限オートマトンでもあるので、こちらで提示しても一切問題ない。
決して、そのまま入れ替えることはしないよう気を付けよう。
おわりに
今回は、非決定性有限オートマトンと決定性有限オートマトンの関係について解説した。
これらで認識できる言語には差がないこと、非決定性から決定性に変換する方法は是非覚えておいて欲しい。
また、補集合は先に決定性に変換してから受理・非受理を入れ替えてあげれば完成する。
直感とは異なると思うので、気を付けよう。
さて、次回はまたしても新しい有限オートマトンが出てくる。
その名も、\(\varepsilon\)入力付き非決定性有限オートマトン。
…名前からどんなものかなんとなく想像できるかもしれないが、色々と定義したいこともある。
その後も使う重要な考え方なので、しっかり身に付けていこう。
オマケで、これも別記事になるが、集合や論理あたりも一度まとめようかと今考えている。
これまで集合をガンガン使っているし、証明の方針も特に解説せずに決めてしまっていた。
そのあたりが不安な方もいらっしゃるかもしれないので、改めて解説しておこう。
2020/12/26追記
次回の内容である、\(\varepsilon\)入力付き非決定性有限オートマトンを解説した。
これまでの内容と混同しないよう気を付けながら進めていこう。
以下がその記事だ。
また、別で進めていた補足シリーズも一旦書き終えた。
初回の集合編をリンクで貼っておくので、そのあたりに自信がない方はそちらも見るといいだろう。



コメント