本シリーズでは、以下の本に沿って解説を書いている。

前回は、ある言語がnfaで認識できるなら、その言語を生成するような正規表現が存在することを示した。
これで、これまで紹介した3種の有限オートマトンと正規表現がそれぞれ同じ言語を構成することが示せた。
証明まで理解できなくともいいが、この事実と、それぞれの変換方法は把握しておこう。
以下が前回の記事だ。
さて、今回は正規言語というやつを見ていこう。
とはいえ、実際は名前の紹介みたいなものだ。
また、全ての言語が正規言語というわけでもない。
そのあたりも少し見てみよう。
正規言語
これまで、言語を表すものとして、以下4つを見てきた。
- dfa : 決定性有限オートマトン
- nfa : 非決定性有限オートマトン
- \(\varepsilon\)nfa : \(\varepsilon\)入力付き非決定性有限オートマトン
- 正規表現
前回まで示してきたり、そして冒頭にも書いたが、これらによって構成される言語には差がない。
この、4種類が構成できるような言語のことを正規言語と呼ぶ。
つまり、例えばある言語が正規言語であることを示せと言われれば、この4種類のどれかでその言語を構成できることを示せばいい、ということだ。
逆に、ある言語が正規言語でないことを示す場合には、いずれかで構成できないことを言えばいい、ということでもある。
これを使って、正規言語の限界について見てみよう。
正規言語の限界
さて、これまで色々な具体例を使ってきた。
例えば、dfaの説明のところでは、0と1の個数がそれぞれ偶数個であるような列からなる言語。
前回は、1と加算記号\(+\)のみからなる数式の言語。
このように、これらで構成できる言語は色々と存在する。
…しかし、実はこれらで構成できない…つまり、正規言語でないような言語ももちろん存在する。
明確にどんな条件なら、ということは触れないが、そんな例を幾つか証明してみよう。
具体例1:括弧の対応
一つ目にこれだ。
先頭から開き括弧がある数だけ並んでいて、その後に閉じ括弧が同じ数だけ並んでいる、という言語。
具体的な列を挙げると、以下のような感じ。
$$\varepsilon, (), (()), ((())), …$$
これが、正規言語でない例の一つ。
さっと証明してみよう。
括弧のままでは分かりづらいので、開き括弧一つを\(0\)に、閉じ括弧一つを\(1\)に置き換える。
すると、この言語\(L\)は、数式で以下のように書き表すことができる。
$$L = \{0^n1^n | n \in \mathbb{Z}, n \geq 0\}$$
では、この言語\(L\)を構成するdfa\(M\)が存在すると仮定しよう。
そう、背理法だ。
さて、この\(M\)の状態数を\(m\)としておく。
そして、初期状態\(s_0\)から、まず列の先頭である\(0\)を読み込んでいこう。
このときの状態を…
- \(s_1 = \delta(s_0, 0)\)
- \(s_2 = \delta(s_1, 0)\)
- …
- \(s_i = \delta(s_{i – 1}, 0)\)
と置いておこう。
さて、列\(0^n1^n\)の\(n\)が\(m\)より大きい場合を見てみる。
このとき、状態数が\(m\)なので、鳩ノ巣原理から\(s_1\)から\(s_n\)までのいずれかは重複している。
これを、\(s_l\)と、\(s_{l + k}\)と置く。
ただし、\(k\)は自然数だ。
このとき、列\(0^l1^l\)は言語の定義から受理状態に遷移する。
…のだが、列\(0^{l + k}1^l\)も受理してしまう。
図にすると以下のようなイメージだ。
なお、今考えている\(M\)はdfaではあるが、以下の図では全ての状態遷移を書いているわけではないので注意。
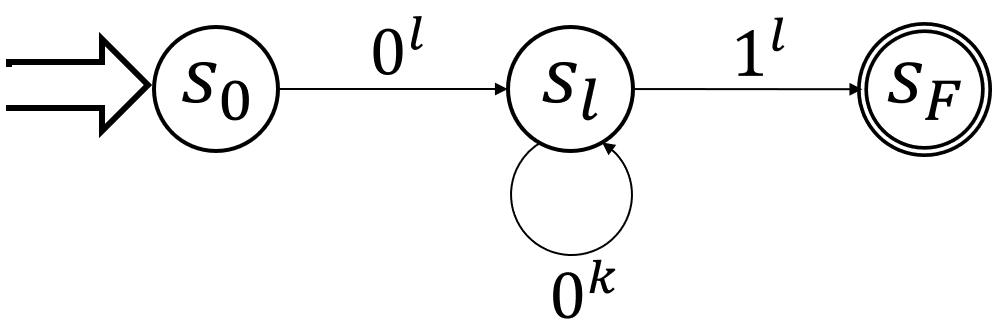
他の遷移は分からないが、とりあえずここの部分だけはこうなっている、という感じだ。
この図から、列\(0^{l + k}1^l\)を受理してしまうことが分かると思う。
一応数式でも書いておこう。
$$\begin{eqnarray}
\delta(s_0, 0^{l + k}1^l) & = & \delta(s_l, 0^k1^l) \\
& = & \delta(s_l, 1^l) \\
& = & s_F \in F
\end{eqnarray}$$
よって、\(M\)は言語\(L\)を認識すると仮定していたが、今それ以外の列を受理できてしまったので、矛盾。
以上から、この言語\(L\)を認識するdfa\(M\)は存在しない。
言い換えれば、この言語\(L\)は正規言語ではないのだ。
具体例2:同じ列の繰り返し
次に、以下のような言語を見てみよう。
$$L = \{xx | x \in \{0, 1\}^*\}$$
何を言っているかというと、アルファベット上の同じ列を2回繰り返したような列からなる言語だ。
これも、正規言語ではない。
上と同じように、証明してみよう。
こちらも背理法を使い、この言語\(L\)を認識するようなdfa\(M\)が存在すると仮定する。
また、この\(M\)の状態数を\(m\)としておこう。
ここで、\(m + 1\)個の記号\(a_1, a_2, …, a_{m + 1} \in \{0, 1\}\)を用意する。
これを\(M\)に入力すると、これまた鳩ノ巣原理から、途中で必ず同じ状態になる部分が出てくる。
今、初期状態から列\(a_1a_2…a_i\)を読み終えた時の状態と、列\(a_1a_2…a_ia_{i + 1}…a_{i + j}\)を読み終えた時の状態が一致しているとする。
このとき、まず列\(a_1a_2…a_ia_1a_2…a_i\)は仮定から受理される。
そして、\(a_1a_2…a_ia_{i + 1}…a_{i + j}a_1a_2…a_i\)も受理されてしまう。
ここで、例えば\(a_1\)のみ\(1\)で、他は\(0\)だったとする。
すると、一つ目の列は先頭が\(1\)、そこから\(i – 1\)個の\(0\)、という内容が2回繰り返される列になる。
そして、二つ目の列は先頭が\(1\)、そこから\(i + j – 1\)個の\(0\)、1個の\(1\)、\(i – 1\)個の\(0\)という列になる。
0の部分に注目すると、\(j > 0\)より必ず\(i + j – 1\)の方が大きくなる。
つまり、同じ列の繰り返しとはなり得ない。
よって、\(L\)に属さない列も受理してしまうので、矛盾だ。
以上からこのような\(M\)は存在せず、言語\(L\)は正規言語でないことが示せた。
具体例3:正規表現
実は、正規表現自体も正規言語ではない。
注意して欲しいのは、正規表現で表現できる言語ではなく、その正規表現自身のことを言っているということ。
なお、実際はどちらでも同じことなのだが、簡略化のためにここでは括弧が省略されていない正規表現を前提とさせてもらう。
例えば、\(\{0, 1\}\)上の正規表現を見てみると…
$$\varepsilon, 0, 1, (0 + 1), (((0)^*) + 1), ((((1 + 0)1) + 0)^*), …$$
などなど。
これらを列として構成される言語は正規言語ではない、ということだ。
これも、上までと同じような方法で証明できる。
まず、正規表現を列とし、それによって構成される言語を認識するdfa\(M\)が存在すると仮定する。
この状態数を\(m\)とする。
今、先頭から括弧が\(m+1\)回出てくるような正規表現を考えてみる。
これを\(M\)に入力すると、これまた鳩ノ巣原理で括弧の途中で同じ状態になる部分が出てくる。
例えば自然数\(i, k\)を使って、\(i\)個目と、\(i + k\)個目で同じ状態だとしよう。
すると、今考えた正規表現は仮定から受理される。
…のだが、この最初の括弧を\(k\)個減らしたものも受理されてしまう。
開き括弧だけ減らしたので、もはや括弧の対応は取れていないことは明らかなのだが、それでも受理してしまっているので、矛盾だ。
よって、正規表現は正規言語ではない。
個別で証明はしないが、括弧を考えた数式も同じ理由で正規言語ではない。
つまり、この講座を始めたきっかけである数式をプログラムで扱うという要望にはまだ応えられていない。
じゃあどうするの?
実は、もうちょっと表現できる言語の幅を広げた、文脈自由言語というものが存在する。
そして、これを構成するような、文脈自由文法というものがある。
これを使うことで、これまで扱うことのできなかった言語の一部が扱えるようになる。
…一部と書いたが、この文脈自由文法も万能ではない。
が、そこまでいくと何章も先になるので、今はこのくらいに留めておこう。
おわりに
今回は、正規言語を簡単にではあるが取り扱った。
とりあえず、これまでやっていたオートマトンや正規表現で作れる言語が正規言語であるということと、それには限界があることを知っておいてもらえれば十分だろう。
さて、次回はようやく参考書でいう次の章に移る。
さっきも名前を出したが、文脈自由文法という内容に入っていこう。
これまでの内容も使わないわけではないので、不安がある場合はしっかり復習しておこう。
2021/1/22追記
次回の内容である、文脈自由文法の解説を公開した。
これまでの内容としっかり区別しておこう。



コメント