本シリーズでは、以下の本に沿って解説を書いている。

前回は、nfaと\(\varepsilon\)nfaで認識できる言語に差がないことを示した。
これで、dfa、nfa、\(\varepsilon\)nfaの3つそれぞれで認識できる言語に差がないことを示せたことになる。
証明が理解できなくとも、この定理はしっかり把握しておこう。
前回の記事は以下だ。
さて、今回は同じような定理をもう一つ証明する。
何かというと、だいぶ前に解説した正規表現から生成される言語と、今書いた3タイプの有限オートマトンで認識できる言語に差がない、という定理。
そのうち、まず正規表現から生成される言語を有限オートマトンで認識できることを示していく。
逆方向の証明が複雑になりそうだったので、二回に分けたというわけだ。
落ち着いて、ゆっくり進めていこう。
ちなみに、正規表現って何だっけという方は、本文中でも定義を再掲するが、以下の記事も併せて見ておくといいだろう。
復習:正規表現
上にリンクを貼ったばかりだが、正規表現を復習しておこう。
\(\Sigma\)をアルファベットとし、\(\Sigma\)上の正規表現\(S\)と、その正規表現から生成される言語\(L(S)\)を以下で定義する。
- \(\phi\)は正規表現であり、\(L(\phi) = \phi\)である。
- \(\varepsilon\)は正規表現であり、\(L(\varepsilon) = \{\varepsilon\}\)である。
- 任意の記号\(a \in \Sigma\)は正規表現であり、\(L(a) = \{a\}\)である。
- \(R_1\)、\(R_2\)を正規表現としたとき、以下3つを定義する。
- \((R_1 + R_2)\)は正規表現であり、\(L((R_1 + R_2)) = L(R_1) \cup L(R_2)\)である。
- \((R_1 \cdot R_2)\)は正規表現であり、\(L((R_1 \cdot R_2)) = L(R_1)L(R_2)\)である。
ただし、この\(\cdot\)は省略してもよい。 - \((R_1^*)\)は正規表現であり、\(L((R_1^*)) = L(R_1)^*\)である。
基本的な事項を定義1から3で決めておき、定義4の三つを使って再帰的に正規表現とそれが生成する言語を決定している形だ。
また、この定義のままだと括弧の数がえげつないことになるので、優先順位を決めて省略できることにしていた。
その優先順位は、高い順に\({}^*, \cdot, +\)。
ただし、これを無視して高い優先度で見たい場合には、そこの括弧を残すこととしていたことも思い出そう。
とはいえ、この優先順位や括弧の省略については表記上の問題で、今回の記事では使用しない。
今回証明する定理
正規表現の復習が終わったところで、改めて今回証明する定理を。
言語\(L\)がある正規表現\(S\)から生成されるとき、その言語\(L\)を認識する\(\varepsilon\)nfaが存在する。
冒頭にも書いた通り、3タイプの有限オートマトンはいずれも認識できる言語に差がないので、そのうち一つだけで示すことができればOKだ。
この証明の方針としては、正規表現から実際に\(\varepsilon\)nfaを作り、それが\(L\)を認識することを示していく。
もうちょっと具体的に書くと、以下のような流れだ。
- (初期段階)一番細かい単位では成り立つことを示す
- (帰納段階)ある時点で成り立つことを仮定し、それより一つ大きい単位で成り立つことを示す
ちょっと分かりにくいかもしれないが、帰納法だ。
では、始めていこう。
初期段階
ここでは、正規表現の定義のうち、定義1から3の内容それぞれについてを示していく。
実際に作成する\(\varepsilon\)nfaを\(M = (K, \Sigma, \delta, s_0, F)\)とし、状態の集合と受理状態の集合は以下で共通としよう。
- \(K = \{s_0, s_1\}\)
- \(F = \{s_1\}\)
入力記号の集合\(\Sigma\)は正規表現のアルファベットと同一だ。
では、順番に見ていく。
まず、正規表現\(S = \phi\)の時、言語は\(L = \phi\)だ。
この時は、状態遷移関数を定義しない。
すると、任意の列を読み込んでも受理状態に遷移できないので、\(L(M) = \phi\)、成立。
次に、正規表現\(S = \varepsilon\)の時、言語は\(L = \{\varepsilon\}\)。
この時は、状態遷移関数を以下のように定義する。
$$\delta(s_0, \varepsilon) = \{s_1\}$$
すると、何も入力されていない状態では受理状態の\(s_1\)に遷移でき、何か一つでも記号を読み込んだ瞬間に遷移先がなくなり、受理しなくなる。
よって、\(L(M) = \{\varepsilon\}\)となり、これもOK。
そして、任意の記号\(a \in \Sigma\)について、正規表現\(S = a\)の時、言語は\(L = \{a\}\)となる。
この時の状態遷移関数は、以下を定義。
$$\delta(s_0, a) = \{s_1\}$$
こうすれば、記号\(a\)を一つだけ読み込んだ時に限り受理状態に遷移する。
つまり、\(L(M) = \{a\}\)、成立。
以上より、定義1から3の形になっている場合は成立することが分かった。
これで、初期段階の証明は完了だ。
…なのはいいが、一つポイントがある。
それは、どれも受理状態がただ一つだけということ。
後でこの\(M\)を一部に持つような\(\varepsilon\)nfaを構成するが、その時に初期状態と受理状態が重要になる。
これを頭の片隅に置いておいて欲しい。
帰納段階
では、次の段階に進もう。
今、帰納法の仮定として、二つの正規表現\(R_1\)、\(R_2\)について、それぞれが生成する言語を認識する\(\varepsilon\)nfaが存在するとしよう。
その\(\varepsilon\)nfaについて、\(R_1\)に対応するものは\(M(R_1) = (K_1, \Sigma, \delta_1, s_0, \{s\})\)、\(R_2\)に対応するものは\(M(R_2) = (K_2, \Sigma, \delta_2, t_0, \{t\})\)と表記する。
各状態については、\(K_1 = \{s_0, s_1, …, s_n = s\}\)、\(K_2 = \{t_0, t_1, …, t_m = t\}\)と置こう。
上に書いたように、両方とも受理状態の集合はただ一つの状態のみを含んでいることに注意だ。
これを前提とし、この二つの正規表現を組み合わせてできる正規表現が生成する言語を認識する\(\varepsilon\)nfa\(M\)を作っていこう。
もちろん、この\(M\)も受理状態はただ一つ。
そうすれば、前提を満たすようになるので、繰り返し同じ方法で拡張していくことができる。
定義4の三種類それぞれについて見ていく。
まず、正規表現\(S = (R_1 + R_2)\)について。
状態の集合は両方の状態の和集合にさらに2状態を追加、\(K = K_1 \cup K_2 \cup \{ss, tt\}\)。
初期状態は今追加した\(ss\)、受理状態の集合はこれまた今追加した\(\{tt\}\)となる。
状態遷移関数について、まず両者の定義をそのまま全て取り入れる。
その上で、以下3定義を追加。
- \(\delta(ss, \varepsilon) = \{s_0, t_0\}\)
- \(\delta(s, \varepsilon) = \{tt\}\)
- \(\delta(t, \varepsilon) = \{tt\}\)
図に書くと以下のような感じだ。
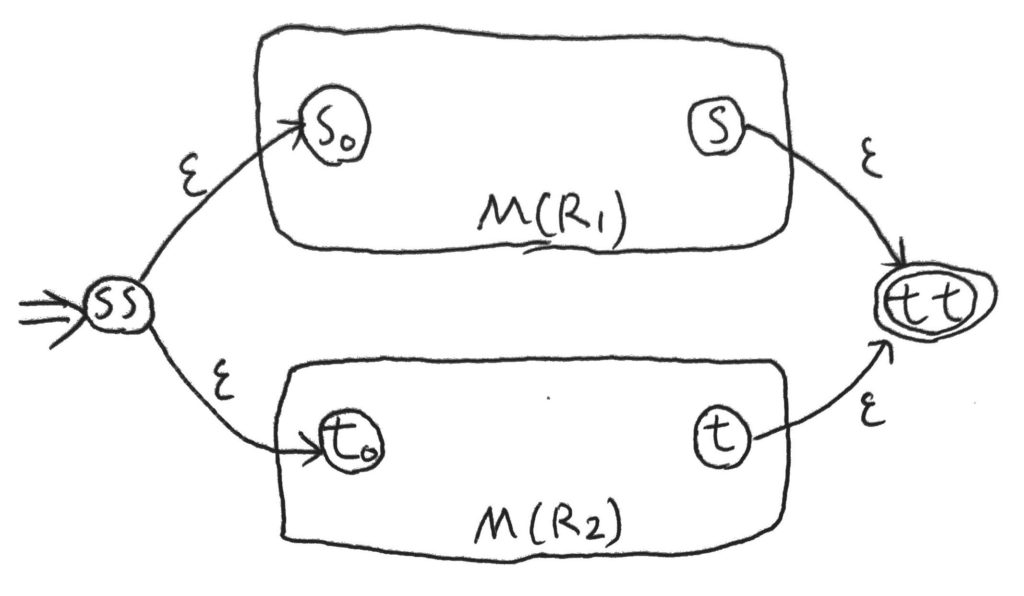
こうすることで、\(M(R_1)\)、\(M(R_2)\)いずれかで受理できれば、全体で受理できる。
ほぼ自明なので、そこは割愛しよう。
ということで、このパターンはOKだ。
次に、正規表現\(S = R_1R_2\)について。
状態の集合は両方の状態の和集合、\(K = K_1 \cup K_2\)。
初期状態は\(M(R_1)\)の初期状態\(s_0\)、受理状態の集合は\(M(R_2)\)の受理状態の集合\(\{t\}\)だ。
そして、状態遷移関数はまず両者の定義を取り入れ、その上で以下一つを追加する。
- \(\delta(s, \varepsilon) = \{t_0\}\)
図だと以下のようなイメージ。
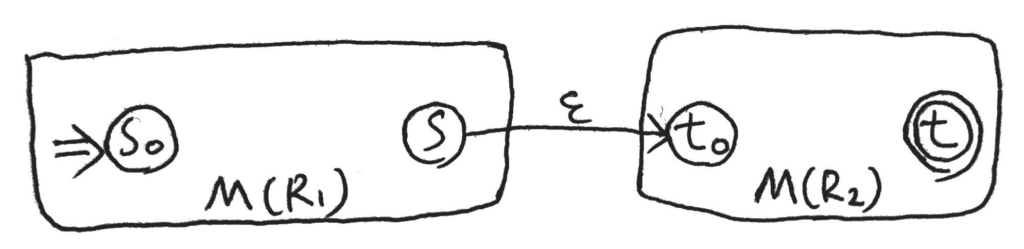
これで、列を前半、後半の二つに分けたとき、前半を\(M(R_1)\)、後半を\(M(R_2)\)で受理できれば、全体でも受理可能。
ここも割愛させてもらうが、これで二つ目のパターンもOK。
最後、正規表現\(S = (R_1^*)\)を見よう。
これは、状態遷移関数以外は\(M(R_1)\)のまま。
状態遷移関数は、以下二つを追加してあげる。
- \(\delta(s_0, \varepsilon) = \{s\}\)
- \(\delta(s, \varepsilon) = \{s_0\}\)
これを図にすると以下。
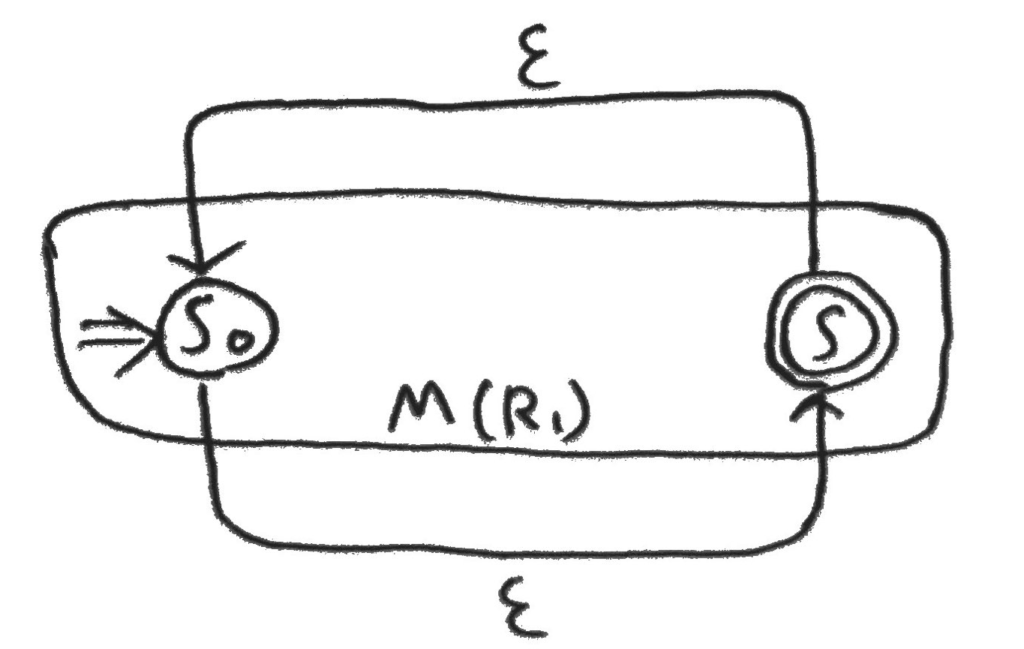
これで、何も読み込まなくても受理状態に行けるし、一回受理状態になるような列の繰り返しを入力しても再度初期状態に遷移することで何度でも受理状態に到達できる。
よって、これもOK。
3パターンとも成立したので、帰納段階が示せた。
以上で、帰納法より、定理の証明が完了だ。
具体例で見てみよう
さて、やってみたはいいものの、具体例がないとなかなか難しいと思う。
そこで、以下の正規表現を実際に\(\varepsilon\)nfaに変換してみよう。
$$S = ((0 + (1 \cdot 1))^*)$$
正規表現の解説の際に出していた例だ。
まず変換する前に、細かい単位に分解していこう。
一つ目、\(R_1 = (0 + (1 \cdot 1))\)とする。
$$S = (R_1^*)$$
二つ目、\(R_2 = 0\)、\(R_3 = (1 \cdot 1)\)。
$$R_1 = (R_2 + R_3)$$
三つ目、\(R_4 = 1\)、\(R_5 = 1\)。
$$R_3 = (R_4 \cdot R_5)$$
これ以上は分解できないので、ここまでにしよう。
では、逆に細かい単位から\(\varepsilon\)nfaを作っていく。
添え字を先頭から順番にしたいので、中途半端なところから始まるが気にしないで欲しい。
まず、\(M(R_4)\)と\(M(R_5)\)は状態名が異なるだけで同型になり、以下のような形になる。

次に、これらを含む\(M(R_3)\)。
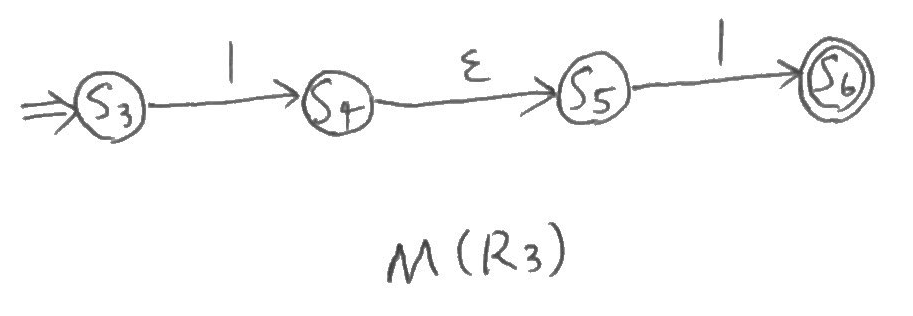
そして、ちょっと別で\(M(R_2)\)を出しておこう。
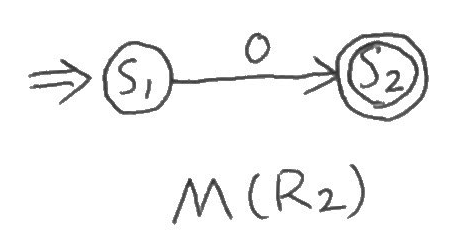
\(M(R_2)\)と\(M(R_3)\)を組み合わせた\(M(R_1)\)。
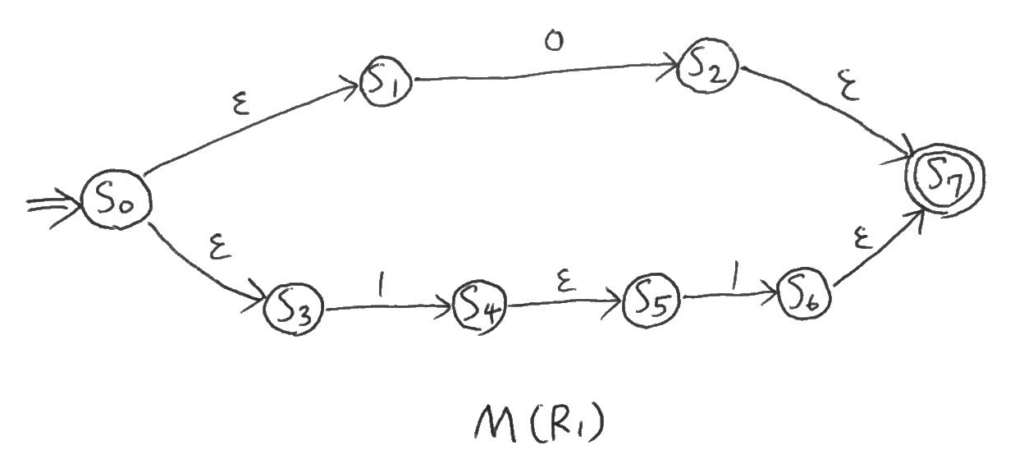
最後、\(M(S)\)は以下のような形。
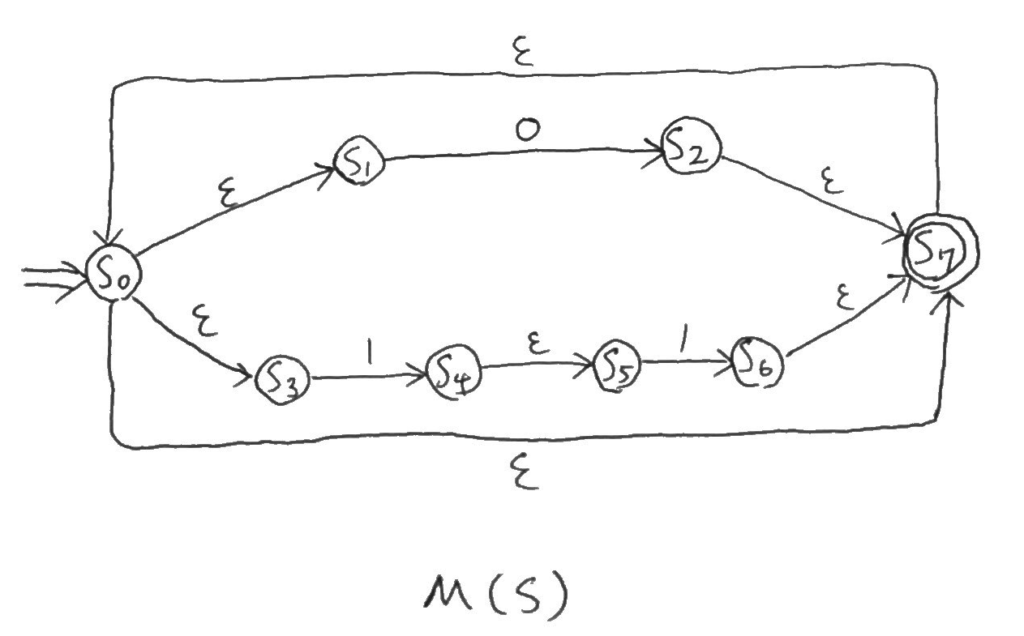
これで、正規表現\(S\)で生成された言語を受理する\(\varepsilon\)nfa\(M(S)\)の完成だ。
心配であれば、実際に正規表現から列を生成し、それを受理するか確認してみてほしい。
おわりに
今回は、正規表現で生成可能な言語について、それを認識するような\(\varepsilon\)nfaが存在することを示した。
そんなに難しくなかったと思う。
…問題は、次回の逆方向の証明だ。
まだ軽く見た程度だが、なかなかに複雑そうだったので、できる限り分かりやすく解説していきたい。
2021/1/21追記
次回の内容を更新して、こちらに追記するのを忘れていた…申し訳ない。
予告通り、今回とは逆方向の証明を行った。
なかなかに難しいので、最悪理解できなくとも、変換方法は覚えておきたい。




コメント