本シリーズは、論理回路で電卓を作ろうと思い、そのために勉強した結果を残しているものだ。
前回は、同期式フリップフロップの使用例として、カウンタと呼ばれる回路を作成した。
特定の信号が0→1になった回数を記録する回路だ。
また、それを使って順序回路としての乗算・除算回路も作成した。
そちらは今後使わないが…まあ、そんなこともできるのか程度に思ってもらえれば大丈夫だ。
以下がその記事だ。
さて、今回は乗算回路を組み直す。
というのも、当初は前回作ったものを使う予定で考えていたのだが、必要なクロックの回数が計算によって変わるのはあまり良くないだろう。
そこで、組合せ回路として…つまり、クロック不要で答えを出すように作り直していこう。
…除算については、記事が長くなる予感がしたので、次回に分けることにする。
組合せ回路での乗算作成方針
まずは方針から。
とはいえ、この方針自体は非常に単純なものだ。
イメージは、筆算。
さすがに筆算自体は分かると思うので、2進数版の筆算から試してみよう。
例えば、1001と0110という2数を乗算してみる。

まあ、通常の10進数における筆算と同じやり方だ。
後者の下の桁から順番に前者の数を掛け合わせ、それをずらしながら配置する。
そして、その結果を(桁に注意しながら)全て足し合わせることで乗算の完了となる。
考え方自体はこれだけで、非常にシンプルなことが分かるだろう。
回路の作成
では早速、回路を作っていこう。
一旦入力は2つの4桁2進数で計8個、出力は全て表せるように用意したい。
4桁の2進数最大値は\((1111)_2 = (15)_{10}\)なので、出力の最大値は\((15^2)_{10}=(225)_{10} = (11100001)_2\)だ。
そのため、8桁用意すれば問題ないだろう。
先ほど書いた方針通りに作成していく。
筆算の中段部分の回路
まずは、中段部分から作成していこう。
まあ、1桁同士の2進数の乗算は両者が1の時のみ1なので、シンプルに各桁をANDで取っていけばいいだろう。
とはいえ、最終的な回路にそのまま書くと図が非常に大きくなりそうなので、ここだけで中間回路を作成する。
入力は5つ、乗算する数の片方\(I_1 = I_{13}I_{12}I_{11}I_{10}\)ともう片方の1桁\(I_{2n}\)、出力は4つでその桁に対応する途中結果\(O’_n = O’_{n3}O’_{n2}O’_{n1}O’_{n0}\)。
シンプルにANDを取ればいいので、各出力は以下の式で表すことができる。
$$O’_{nm} = I_{1m}I_{2n}$$
これを図にすると以下の通りだ。
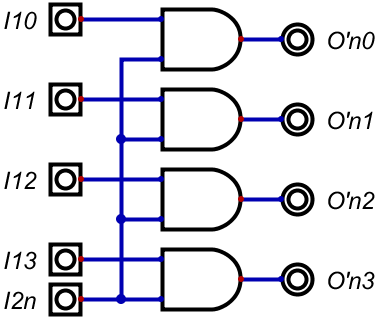
ここはそんなに難しくないので大丈夫だと思う。
中段部分の和
さて、頭を使わなければいけないのはここだろう。
今、中段部分の各行は上の回路で得ることができた。
あとは、それらをずらしながら全て足し合わせるだけだ。
ここで、考え方を少し変えてみよう。
筆算では、最下位の桁から順に足し、繰り上げも考えながら結果を求めていた。
これを、中段の行を1行ずつ足していく、と考えなおす。
どういうことかというと、例えば\((1011)_2 \times (0110)_2\)という計算を例に考えてみる。
まず、中段までの筆算を以下に出そう。
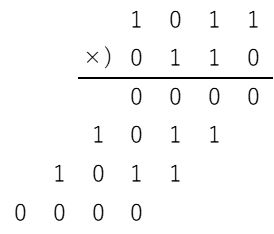
ここで、何もせずとも最下位の結果は出ている。
中段一行目の一番右、0が最下位の結果だ。
次に、1行目と2行目を、桁に注意しながら加算する。
すると、以下のようになる。
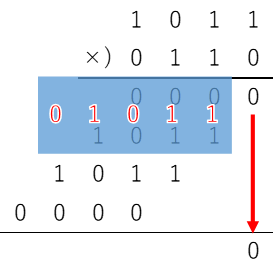
4桁の加算なのだが、出力は上位桁へのキャリー(上の図だと青枠内一番左の0)も必要になるので注意。
これで、下から2桁目も1で確定した。
今度は、今足した部分とさらに次の1行を、同じように足す。
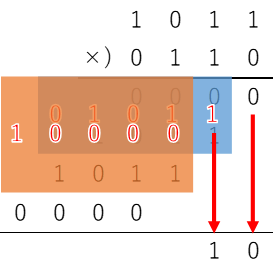
また1つ、桁が確定。
そして、残りは足した結果がそのままそれぞれの桁の結果になるので…
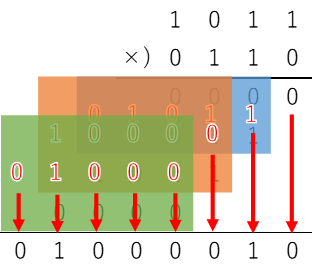
これで、最終的に答えを出せた。
このように、各桁を1つずつずらしながら加算していけばOKだ。
一つ注意としては、上にも書いたが以前作成した4桁加算器そのままではなく、上位桁へのキャリー\(C\)も必要になること。
出力を一つ増やすだけなので具体的な回路図は載せないが、名前は作り直しと付けておいた。
これを踏まえ、回路全体を組んだものが以下だ。
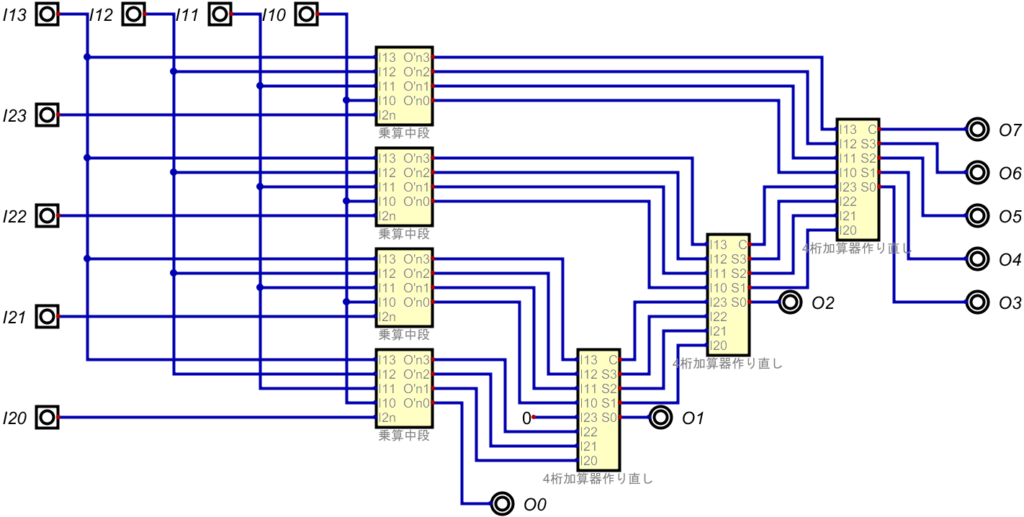
これで、組合せ回路版の乗算器の完成だ。
ちなみに、1つ補足で一番下にある4桁加算器の\(I_23\)への入力。
ちょうど、出力\(O_1\)の加算器を挟んで反対側に出ている部分だ。
ここに入っている「0」という記号は、常に0を出力しているものだと思ってほしい。
幾つか具体的な数で計算してみて、合ってそうなことは確認できた。
おわりに
冒頭にも書いた通り、除算器の方が厄介なイメージがあったので、一旦今回はここまでにしよう。
作って思ったのだが、最初考えていたよりはだいぶスッキリまとまった印象がある。
もちろん、実際に電卓を作る際も乗算器はこの形を採用しよう。
なお、桁数を増やす時も同じ考え方で可能だ。
さて、次回は除算器を同じく組合せ回路として作成してみる。
考え方(というか方針)も似ているため、その気がある方は一度自分で組んでみるのも面白いだろう。




コメント
続きまってます!