前回は、二つ目の高速なソートアルゴリズムであるマージソートを解説した。
残る、高速なソートアルゴリズムは一つだ。
今回は、その残っているヒープソートを解説していこう。
…とはいっても、実は今回ほとんど解説することがない。
どういうことか含め、本文中で説明をしていこう。

分かりやすいけど組みにくい、
そんな印象を受けたよ
前提知識
今回は、以下の知識が必要になる。
- ヒープ
そう、今回のヒープソートとは、このヒープというやつを使うソートなのだ。
というわけで、そちらは以前の解説をご参照頂きたい。
【連結リスト・ヒープ】高速なソートアルゴリズム前提知識 -データ構造編- | Shino’s Mind Archive
ヒープソート
上でちらっと書いてしまったが…
ヒープソートとは、データ構造であるヒープを使用したソートのこと。
いったんヒープを構成すれば、最小要素を取り出して再構成する、という動作を繰り返すだけで、ソートが完了してしまう。
その最小要素は一番上に来ているので、それを順番に取り出せば完了だ。
…実は、これで説明終わり。
ただ、プログラムを組むときにちょっとコツがいるので、今回はそちらの説明を厚くしておこう。
ヒープソートの計算量
高速なアルゴリズムに分類されている通り、ある程度高速にソートができる。
計算量は、\(O(n \log(n))\)だ。
なお、本来であれば、ヒープを構成する用の領域が必要になる。
だが、プログラムをうまいこと組めば、その領域もいらなくなる。
今回のサンプルでは、このうまいこと組んだものを提示しよう。
ヒープソートのサンプルプログラム
では、そのサンプルプログラムだ。
…の前に、一個だけ先に補足を。
ヒープをどのようにプログラムで構成するか、という問題だ。
前提知識の記事に書いた通り、配列だけで実現ができる。
その実現方法は、図にすると以下のような感じになる。
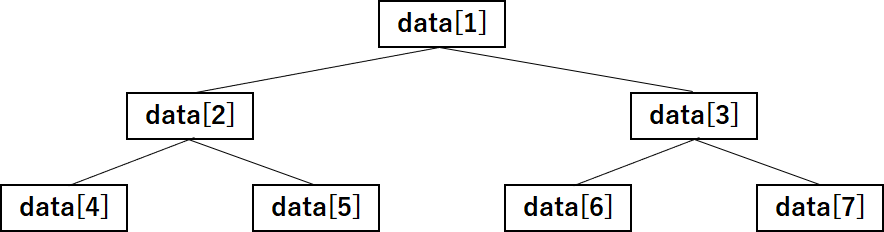
このように、添え字を1から開始して、上から順番に敷き詰めるように配置する。
そうすると、ある要素の子が表しやすくなるのだ。
ある要素iの子は、必ずi * 2とi * 2 + 1で表せるのが分かるだろうか。
こうすることで、うまくプログラムで扱えるようになる。
これを確認したうえで、サンプルソースは以下の通りだ。
function downheap(data, from, to){
let val = data[from];
let i = from;
while(i <= Math.floor(to / 2)){
let j = i * 2;
if(j + 1 <= to && data[j] <= data[j + 1]){
j++;
}
if(val > data[j]){
break;
}
data[i] = data[j];
i = j;
}
data[i] = val;
}
function HeapSort(data){
let n = data.length;
for(let i = n; i > 0; i--){
data[i] = data[i - 1];
}
data[0] = 0;
for(let i = Math.floor(n / 2); i >= 1; i--){
downheap(data, i, n);
}
for(i = n; i >= 2; i--){
let tmp = data[1];
data[1] = data[i];
data[i] = tmp;
downheap(data, 1, i - 1);
}
}メインの処理は、下にあるHeapSort()。
添え字を1から始めるため、ちょっとデータに手を加えてから処理を開始する。
どのように処理をしているかというと、まず右下の部分から順番に、部分的なヒープを構成していく。
上の図でいうdata[3]、data[6]、data[7]の部分だけヒープにするイメージだ。
これを、一つずつずらしながらヒープを構成していく。
そして、全部終わった段階で、この構造自体がヒープとなる。
downheap()という処理が入っているが、ちょっと飛ばして先に全体像を。
ヒープを構成した後、まず根にあたるdata[1]を、一番後ろのデータと入れ替える。
そして、その状態で、末尾を除いた部分でもう一度ヒープを構成する。
次に、また根にあたるdata[1]を、後ろから2番目と入れ替えて、この二つを除いた部分で再度ヒープを構成する。
これを繰り返すことで、最終的に並び替えていくのだ。
では、飛ばしたdownheap()の説明を。
これは、指定した範囲で、根にあたる要素を適した箇所まで沈める処理だ。
これを、範囲を指定しながら呼び出すことで、部分的なヒープを構成できるようになっている。
さて、勘のいい方なら、違和感を覚えていると思う。
最小の要素から順番に末尾に入れていっているので、逆順になるのでは…?ということだ。
実際、その通り。
普通にヒープを構成してしまうと、根には最小となる要素が浮かび上がってくる。
そのため、そこから末尾に入れているので、ソートが降順となるのだ。
これを防いで昇順にするために、今回のヒープは根が一番大きくなるよう、条件を変えている。
ただヒープを作りたい場合は、7行目、10行目の比較を変えてあげれば大丈夫だ。
おわりに
考え方は簡単だが、ソースを組む際には気を付けなければならないことが多いソートだったように思う。
というわけで、今回はヒープソートを解説してきた。
構造の意味さえ分かっていれば、直感的にはわかりやすいのかなという印象だ。
さて、次回以降どうするかは現在模索中だ。
他に解説した方が良さそうなソートなどあれば、解説するとしよう。



コメント