本シリーズでは、以下の本に沿って数学を解説している。
前回は微分編第三回、多変数関数の微分について解説した。
多変数関数については、その独立変数の一つに着目し、それ以外を定数として見なして微分する偏微分という方法を使う。
今回の内容にも出てくるので、復習しながら進めていこう。
以下がその記事だ。
今回は、勾配降下法というものを解説する。
先に意味と公式を紹介し、なぜそうなるのかを説明する形にしよう。
勾配降下法
いきなりだが、この勾配降下法で何ができるかから解説を始めていこう。
なお、前回から引き続き、まずは2変数関数の場合で解説し、その後多変数に拡張しよう。
ある関数\(z = f(x, y)\)が与えられ、この\(z\)を最小にするような変数\(x\)、\(y\)の値を求めたいとしよう。
このときに、この勾配降下法というものを使う。
イメージは、ある時点での現在地の座標を\((x, y, z)\)としよう。
このとき、\(z\)が小さくなるように、\(x\)、\(y\)を少しずつ動かしていくのだ。
公式は、この少しずつ動かす\(x\)、\(y\)の変化量を求めるものになる。
この動かす量を、それぞれ\(\Delta x\)、\(\Delta y\)と置こう。
この二つは、以下の式で求めることができる。
$$(\Delta x, \Delta y) = -\eta(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})$$
この中の\(\eta\)は正の小さい定数で、これを調整すると、一度の移動でどの程度動かせるかを変えることができる。
言葉で説明すると、各独立変数を動かす量は、その変数で偏微分したものに\(-\eta\)を掛けることで求められる。
3変数以上でも、同じ言葉の説明になる。
この式を使って求めた\(\Delta x\)、\(\Delta y\)を元の\(x\)、\(y\)に足すことで、より小さい\(z\)を求めることができる。
これを繰り返し、\(\Delta x\)、\(\Delta y\)が0になれば、そこが最小だ、ということだ。
さて、いきなりこんなことを言われてもわけがわからないと思う。
そこで、なんでこの方法、式で求められるのかを解説していく…のだが。
多変数関数の最小の条件
その前に、1変数関数で考えていた関数の最小を、2変数関数に拡張しておこう。
もちろん、3変数以上でも同じだ。
1変数関数における最小の条件は、その導関数の値がゼロであるということだった。
これを2変数関数に拡張すると、以下のようになる。
関数\(f(x, y)\)が最小となるとき、以下の2式が成り立っている必要がある。
$$\frac{\partial f(x, y)}{\partial x} = 0, \frac{\partial f(x, y)}{\partial y} = 0$$
要するに、関数が最小となるためには、各独立変数それぞれで偏微分した結果がゼロになっている必要があるのだ。
逆が成り立つとは限らないのも1変数の時と同じ。
試しに、簡単な2変数関数\(z = x^2 + y^2\)における最小値を求めてみよう。
ぱっと見で\(x = y = 0\)のときに\(z = 0\)で最小というのは分かるが、練習で上の条件を使ってみよう。
まず、\(x\)、\(y\)それぞれで偏微分してみる。
$$\frac{\partial z}{\partial x} = 2x$$
$$\frac{\partial z}{\partial y} = 2y$$
ということで、両方とも0であれば導関数が0になる。
それ以外では0にはならず、\(z\)の値は増えてしまうので、両方とも0の場合に関数が最小となることが分かった。
ということで、これを満たす箇所を見れば…といきたいところだが、実際にはこれを解くことが難しい場合がある。
そういう時に、直接求めるのではなく、繰り返し計算して手探りで求めていく、というのが勾配降下法になる。
関数の近似公式
勾配降下法の式を出す際の出発点になるのが、この関数の近似公式というものだ。
まずは、1変数で考えよう。
先に、導関数の定義を再掲しておく。
$$f'(x) = \lim_{\Delta x \to 0}\frac{f(x + \Delta x) – f(x)}{\Delta x}$$
これについて、リミットを取っ払って、\(\Delta x\)を小さい値とする。
すると、以下の近似式が得られる。
$$f'(x) \sim \frac{f(x + \Delta x) – f(x)}{\Delta x}$$
これを変形すると以下の形になり、これが1変数関数の近似公式というものだ。
$$f(x + \Delta x) \sim f(x) + f'(x)\Delta x$$
これを、2変数に拡張すると、以下の通り。
$$f(x + \Delta x, y + \Delta y) \sim f(x, y) + \frac{\partial f(x, y)}{\partial x}\Delta x + \frac{\partial f(x, y)}{\partial y}\Delta y$$
もうちょっと変形を行う。
今、関数\(f(x, y)\)を\(z\)と置き直そう。
そして、\(x\)、\(y\)が変化した際の関数の変化量を、\(\Delta z\)とみなす。
式で表すと、\(\Delta z = f(x + \Delta x, y + \Delta y) – f(x, y)\)だ。
これを使うと、近似公式が以下の形に変形できる。
$$\Delta z \sim \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y$$
かなり綺麗な形になった。
近似式をベクトルの内積として捉える
さて、近似式の右側は、ベクトルの内積と捉えることができる。
具体的には、以下二つのベクトルだ。
$$(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y})$$
$$(\Delta x, \Delta y)$$
ちょっと、状況を整理しよう。
最終的にやりたいことは、元の関数\(z = f(x, y)\)を最小にしたい、ということだった。
そして、今二つのベクトルの内積で求められるのは、関数の変化量\(\Delta z\)。
よって、この内積が最も小さくなるように二つ目のベクトルの値を決定すればよい。
では、ベクトルの内積を思い出してみよう。
二つのベクトルの内積が最小となる条件はというと、この二つのベクトルの向きが真逆を向いているときだ。
つまり、\(\eta\)を正の数として、以下の関係式が成り立っているときに、内積が最小となる。
$$(\Delta x, \Delta y) = -\eta(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})$$
逆に言えば、この式を満たすよう\(\Delta x\)、\(\Delta y\)の値を決めてあげれば、関数の値はどんどん小さくなるはずだ。
これこそが、勾配降下法の考え方になる。
紹介の最後に、3変数以上の場合に拡張しておこう。
関数\(y = f(x_1, x_2, …, x_n)\)に対する勾配降下法の公式は以下の通りだ。
$$(\Delta x_1, \Delta x_2, …, \Delta x_n) = -\eta (\frac{\partial y}{\partial x_1}, \frac{\partial y}{\partial x_2}, …, \frac{\partial y}{\partial x_n})$$
勾配降下法を使う際のステップ
では、具体的な関数に対してこの勾配降下法を使ってみよう。
先に、方針を全てまとめてしまう。
- 事前に、関数を各独立変数で偏微分しておく
- 定数\(\eta\)の値と、初期の各独立変数の値を決める
- 以下の内容を、各独立変数の変化量の値が0になるまで続ける
- 現在の各独立変数の値から、それぞれの変化量を求める
- 変化量として求まった値を、各独立変数に足す
- その時点での各独立変数の値のときに関数値が最小となるとして出力する
こんな感じになる。
対象となる関数は、\(z = x^2 + y^2\)とする。
上で一回求めているので、本当に求まるのかを確認しやすいだろう。
では、ステップ1として、先に偏微分をしてしまおう。
$$\frac{\partial z}{\partial x} = 2x$$
$$\frac{\partial z}{\partial y} = 2y$$
次にパラメータと初期値だが、\(\eta = 0.1\)、\(x = 5\)、\(y = 4\)とでもしておこう。
ここから、ひたすら計算だ。
最初一回分の計算の様子だけお見せしよう。
まず、各独立変数の増分を求める。
ここで、勾配降下法の公式を使用する。
2変数のものを再掲すると、以下の通りだ。
$$(\Delta x, \Delta y) = -\eta(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})$$
まず\(\Delta x\)について、\(x\)で偏微分したものに\(-\eta\)を掛ければいいので、
$$\Delta x = -0.1 \times 2 \times 5 = -1$$
同じように、\(\Delta y\)は、
$$\Delta y = -0.1 \times 2 \times 4 = -0.8$$
と求められる。
まだ0ではないので、次の回のために\(x\)、\(y\)の値を調整しよう。
新しいそれぞれの値は、今求めた変化量を足せばいいので…
$$x = 5 + (-1) = 4$$
$$y = 4 + (-0.8) = 3.2$$
となり、ここからまた変化量を求めることになる。
これを繰り返すと、最終的に\(x = y = 0\)で落ち着くまで求められるので、よかったらExcelなどで計算してみてほしい。
ちなみに、Excelで小数第二位まで表示すると、32回目の計算時点で\(x\)、\(y\)の値が0になる。
勾配降下法の注意点
ここまで、勾配降下法の説明と具体的な使用方法を解説してきた。
で、これを使えば関数の最小値が求められる、とも説明したのだが…実は、状況によっては上手く求められないパターンがある。
どういう状況かというと、極小値が最小値とは別で存在し、その極小値に向かってしまうような状況だ。
具体的に、以下の関数で計算をしてみよう。
$$f(x) = 3x^4 – 4x^3 – 12x^2$$
これは1変数関数だが、勾配降下法はそのまま使える。
なお、グラフを描いてみると以下のようになる。
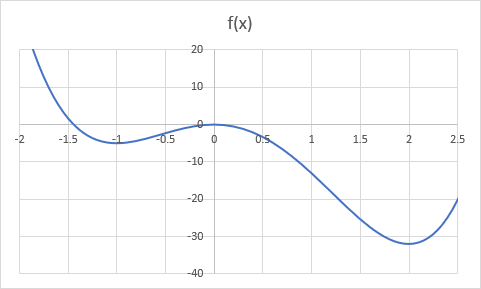
先に、高校の内容を使って最小値を求めてみる。
増減表を書くために\(f(x)\)を微分しよう。
$$f'(x) = \frac{df(x)}{dx} = 12x^3 – 12x^2 – 24x$$
この\(f'(x) = 0\)となる\(x\)を求めると、\(x = 2, 0, -1\)となる。
これを元に、増減表を書くと以下の通りだ。
| \(x\) | … | -1 | … | 0 | … | 2 | … |
|---|---|---|---|---|---|---|---|
| \(f'(x)\) | – | 0 | + | 0 | – | 0 | + |
| \(f(x)\) | ↘ | -5 | ↗ | 0 | ↘ | -32 | ↗ |
この結果より、\(x = 2\)のとき、最小値-32となることが分かる。
では、勾配降下法を使ったパターンで解いてみよう。
微分をした結果は上の通りだ。
各パラメータについて、\(\eta = 0.001\)、\(x\)の初期値は-5としてみよう。
この条件で勾配降下法を使うと、なんと結果が\(x = -1\)のとき-5が最小と出てしまう。
これは、\(\eta\)が小さすぎて、真ん中の山を飛び越えられずに極小値に向かってしまうことが原因だ。
上のグラフで言うと、一番左から近づけていて、真ん中の山を飛び越えられていないイメージだ。
このように、状況によっては上手く求められない場合があることを覚えておこう。
ちなみに、他にもまずい状況はある。
例えば、\(\eta\)の値を0.1とすると、今度は移動距離が大きすぎてグラフの右、左を行ったり来たりして結果的に関数の値が増えていってしまう。
こんな状況になった時は、\(\eta\)や変数の初期値をうまく調整していこう。
なお、今回の場合は、\(\eta = 0.001\)、初期値\(x = 3\)とすれば上手く求められる。
おわりに
今回は、勾配降下法を解説した。
恐らく、一回見ただけでは分からないことが多いと思うので、繰り返し読んで、あるいは他のサイト様も是非参考にしてみてほしい。
また、Excelなどで具体的に使ってみるのもいいだろう。
さて、次回は最適化問題と、その題材として回帰分析を扱う。
メインは回帰分析の解説になると思うが、最適化問題の考え方はニューラルネットワークにも使えるので、ここで感覚を掴んでしまおう。



コメント