本シリーズでは、以下の本に沿って解説を書いている。
前回は、形式言語の形に合わせた正規表現を定義した。
今回はちょっとその範囲から外れるが、後でまた戻ってくるので忘れないようにしてほしい。
以下がその記事だ。
さて、今回は前回解説できなかった有限オートマトンに進んでいく。
記号が増えたり考え方が複雑になったりするが、落ち着いて一個一個見ればそんなに難しくない。
カンタンな例も紹介しながら進めるので、自分のペースで進めていこう。
なお、前回まで形式言語と書いていたところを、今回から単に言語と表記させていただく。
もし自然言語と区別する場合は、補足することとしよう。
有限オートマトン
さて、前回解説した正規表現だが、イメージとしてはこの決まりにしたがって、列を生成していくもの、ということを書いたと思う。
今回扱う有限オートマトンは、逆にすでにある文字列に対し、それが言語に該当するかをチェックするようなイメージになる。
ということで、これも言語の条件を表記する方法の一つだ。
やることのイメージ
先に、どんなことをしていくか、イメージを詳細に書いてみよう。
今、入力となる列\(x\)がテープに書かれていたとする。
これを、機械で先頭から1文字ずつ読み込んでいく。
その際、状態というものを考え、読み込んだ文字によってこの状態を変化させていく。
状態というと難しそうだが、入力記号とは別の数字や文字があって、それが変わっていくところを想像してもらいたい。
そして、入力の列\(x\)を全て読み終えた時に、その時の状態から機械は\(x\)が言語\(L\)に含まれるかどうかを判定する。
こんなことをする機械が、有限オートマトンだ。
このイメージは今後別のオートマトンを考える際には使えないが、今回解説する内容に対しては問題ない。
有限オートマトンの定義
上のイメージでは、有限オートマトンを機械として考えてもらった。
しかし、実際は数学的なモデルだ。
ということで、定義をしていこう。
有限オートマトンは、\(M = (K, \Sigma, \delta, s_0, F)\)という5つの要素の組で与えられる。
また、この有限オートマトン\(M\)で構成される言語を\(L(M)\)としよう。
このそれぞれが何を表しているかは以下の通り。
- \(K\) : 状態の有限集合
- \(\Sigma\) : 入力記号の有限集合(=言語のアルファベット)
- \(\delta\) : 状態遷移関数、\(K \times \Sigma \rightarrow K\)の写像
- \(s_0 \in K\) : 初期状態
- \(F \subset K\) : 受理状態の有限集合
これで定義した有限オートマトン\(M\)に対し、ある列\(x \in \Sigma^*\)を入力したとしよう。
まず、最初の状態を初期状態\(s_0\)とする。
これで、\(x\)の先頭から1文字ずつ読み込んで、状態遷移関数\(\delta\)によって状態を変化させていく。
状態遷移関数\(\delta\)は、ある時の状態を\(s \in K\)、そのときに記号\(a \in \Sigma\)を読み込んで状態\(s’ \in K\)に変化することを以下のように表記する。
$$\delta(s, a) = s’$$
全ての状態に対し、全ての入力記号による遷移を定義するので、括弧内の組合せは入力の数と入力記号の数の乗算だけある。
例えば状態数が4つ、入力記号が2つなら、状態遷移関数は全部で8個定義されている必要がある。
\(x\)の最後まで読み込んだ時、状態が\(s\)だったとしよう。
この\(s\)が\(F\)の要素だったとき、その列\(x\)は\(M\)で受理されるといい、\(x \in L(M)\)だ。
逆に\(s \not \in F\)のときは、列\(x\)は\(M\)で受理されない、\(x \not \in L(M)\)となる。
そして、この\(L(M)\)を、\(M\)が認識する言語、という言い方をする。
これで有限オートマトンが定義された。
…と書いたが、これだけではさっぱりだと思う。
そこで、具体的な内容を使って、実際に有限オートマトンを動かしてみよう。
具体例
有限オートマトンを考えるときは、状態遷移図というものを書くと非常に分かりやすい。
そこで、以下のような状態遷移図で表される有限オートマトン\(M = (K, \Sigma, \delta, s_0, F)\)を考えてみよう。
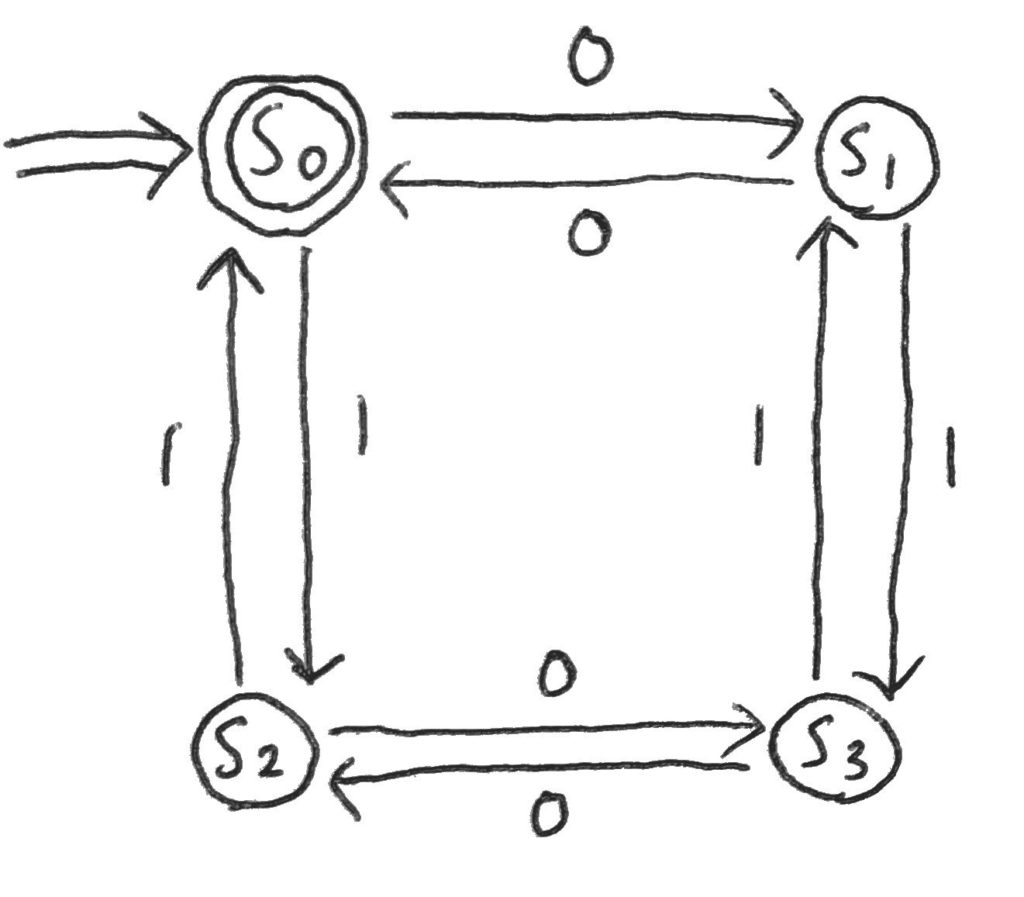
…手書きで汚いが申し訳ない。
が、何が書いてあるかは分かると思うのでこれでやらせてもらおう。
これについて、先に各要素の具体的な内容を書くと以下の通りになる。
- \(K = \{s_0, s_1, s_2, s_3\}\)
- \(\Sigma = \{0, 1\}\)
- \(F = \{s_0\}\)
また、状態遷移関数\(\delta\)は以下の通りだ。
| 現状態\(s\) | 入力\(a\) | 次状態\(\delta(s, a)\) |
|---|---|---|
| \(s_0\) | 0 | \(s_1\) |
| \(s_0\) | 1 | \(s_2\) |
| \(s_1\) | 0 | \(s_0\) |
| \(s_1\) | 1 | \(s_3\) |
| \(s_2\) | 0 | \(s_3\) |
| \(s_2\) | 1 | \(s_0\) |
| \(s_3\) | 0 | \(s_2\) |
| \(s_3\) | 1 | \(s_1\) |
これらと照らし合わせながら、状態遷移図の見方を説明しよう。
まず、\(s_0\)から\(s_3\)が丸で囲まれている。
このそれぞれが\(M\)の状態を表しており、今回は\(K = \{s_0, s_1, s_2, s_3\}\)となる。
次に、\(s_0\)に向かって二重線の矢印が書かれていて、これは初期状態を表している。
そして、状態間に一本線の矢印と、数字の0とか1が書かれている。
これが状態遷移の様子を表している。
例えば、今状態が\(s_1\)で、その時に記号1を読み込むと、次の状態は\(s_3\)になる、ということを表している。
式で書けば、\(\delta(s_1, 1) = s_3\)だ。
これを全て書き出すと、上の表の通りになる。
最後、\(s_0\)だけ二重丸で囲まれている。
これが受理状態を表しており、今回は\(F = \{s_0\}\)となる、ということだ。
今回は一つだが、もちろん複数あっても、もっと言えば空集合でも問題ない。
…が、空集合の場合は任意の列を受理しないため、その時のオートマトンが認識する言語は空集合\(\phi\)となる。
では、実際に列を二つほど読み込んでみよう。
まず、011という列で試してみる。
初期状態は\(s_0\)だったので、先頭から順番に遷移させてみよう。
- \(\delta(s_0, 0) = s_1\)
- \(\delta(s_1, 1) = s_3\)
- \(\delta(s_3, 1) = s_1\)
ということで、全て読み終えた段階で状態は\(s_1\)だ。
これは受理状態の集合\(F\)に含まれないので、この列011は\(M\)で受理されない、つまり\(011 \not \in L(M)\)だ。
次に、0101という列を読み込んでみる。
- \(\delta(s_0, 0) = s_1\)
- \(\delta(s_1, 1) = s_3\)
- \(\delta(s_3, 0) = s_2\)
- \(\delta(s_2, 1) = s_0\)
今度は、最後に\(s_0\)になった。
これは受理状態の集合\(F\)に含まれるため、列0101は\(M\)で受理され、\(0101 \in L(M)\)であることが分かった。
なんとなく、動き方は分かっただろうか。
今回のオマケで、この有限オートマトン\(M\)が認識する言語\(L(M)\)がどんな言語かを説明するので、よかったらそちらも見てみよう。
状態遷移関数の拡張
さて、このままでもいいのだが、一つ拡張をしよう。
状態遷移関数\(\delta\)について、今の定義だと記号\(a \in \Sigma\)による遷移しか使えない。
そこで、列\(x \in \Sigma^*\)を読み終えた際にどこへ遷移するか、というものを表せるよう拡張しよう。
新たに\(\hat{\delta} : K \times \Sigma^* \rightarrow K\)という写像を導入する。
状態を\(s \in K\)、記号(長さ1の列)を\(a \in \Sigma\)、列を\(x \in \Sigma^*\)として以下のように定義する。
- \(\hat{\delta}(s, \varepsilon) = s\)
- \(\hat{\delta}(s, xa) = \delta(\hat{\delta}(s, x), a)\)
これが何を言っているか、これまた具体例で見てみよう。
上の状態遷移図を書いた有限オートマトン\(M\)で、さっきと同じく011を読み込んでみる。
このとき、\(\hat{\delta}(s_0, 011)\)は以下のように計算できる。
まず、定義の二つ目から細かい単位に分解していこう。
- \(\hat{\delta}(s_0, 011) = \delta(\hat{\delta}(s_0, 01), 1)\)
- \(\hat{\delta}(s_0, 01) = \delta(\hat{\delta}(s_0, 0), 1)\)
- \(\hat{\delta}(s_0, 0) = \delta(\hat{\delta}(s_0, \varepsilon), 0)\)
ここで、\(\hat{\delta}(s, \varepsilon) = s\)を使って最後の式が確定する。
これを使って逆順に埋めていくと…
- \(\hat{\delta}(s_0, 0) = \delta(s_0, 0) = s_1\)
- \(\hat{\delta}(s_0, 01) = \delta(s_1, 1) = s_3\)
- \(\hat{\delta}(s_0, 011) = \delta(s_3, 1) = s_1\)
ということで、上で求めた通り\(s_1\)に遷移すると求めることができた。
これで列に対しても一つの数式で書けるようになった…のだが。
ここで、任意の記号\(a \in \Sigma\)に対して…
$$\begin{eqnarray}
\hat{\delta}(s, a) & = & \hat{\delta}(s, \varepsilon a) \\
& = & \delta(\hat{\delta}(s, \varepsilon), a) \\
& = & \delta(s, a)
\end{eqnarray}$$
が成立している。
よって、わざわざこの二つを分けて表記する必要もないだろう。
ということで、ここから特に断りをしなければ\(\hat{\delta}\)を\(\delta\)と書くこととする。
受理する・認識する、を数式で表現
上で列に対する状態遷移関数を定義したので、有限オートマトン\(M\)で受理される列\(x\)やこれが認識する言語\(L(M)\)、というのを数式で書けるようになった。
まず、有限オートマトンを\(M = (K, \Sigma, \delta, s_0, F)\)と置こう。
これに対し、まず列\(x \in \Sigma^*\)が\(M\)で受理されるとは、
$$\delta(s_0, x) \in F$$
と表記できる。
そして、有限オートマトン\(M\)が認識する言語\(L(M)\)は、
$$L(M) = \{x \in \Sigma^* | \delta(s_0, x) \in F\}$$
と書くことができる。
こういった表記は、今後の証明内で使うことになるので、覚えておこう。
加算のみ定義された数式を受理する有限オートマトン
最後に、いつもやっている「足し算だけ定義されている数式」を表す言語を受理するような有限オートマトン\(M\)を考えてみる。
先に、入力記号の集合\(\Sigma\)は以下で問題ないだろう。
$$\Sigma = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +\}$$
初期状態は\(s_0\)としておこう。
先頭は数字が来るはずなので、0から9までの数字を読み込んだら\(s_1\)に遷移するとしておく。
その次も数字であれば同じ状態だ。
で、数字だけであっても問題ないので、\(s_1\)は受理状態の集合\(F\)の要素だ。
また、最初にいきなり\(+\)を読み込んだらアウトなので、その時は\(s_2\)に遷移させておこう。
そして、そこからは何を読み込んでもアウトのままなので、自身に遷移させて、これは受理状態には入れないでおく。
次に、\(s_1\)の状態から\(+\)を読み込んだ場合を考えよう。
一旦、\(s_3\)に遷移するとし、そこからまた数字かプラスかで状態が変わってくる。
この\(s_3\)を読み込んだ時点ではプラスで終わっているので、これは受理状態ではない。
\(s_3\)からまた\(+\)を読み込んでしまうと、プラスが2連続で出てきてしまうので、NG。
このときは\(s_4\)に遷移させて、そこからは何を読み込んでも同じ状態とする。
また、\(s_4\)は受理状態には含まれない。
で、\(s_3\)で数字を読んだ場合には、今度は\(s_5\)に遷移させておく。
数字は何度連続で読み込んでもいいので、\(s_5\)から数字による遷移先は\(s_5\)だ。
ここでは最後が数字なので、受理状態で問題ないだろう。
この\(s_5\)でプラスを読み込んだ場合は問題ないので、また別の\(s_6\)…とする前に。
この後の流れを考えると、プラスを読んだらアウト、数字を読み込んだらOK、と続いていくので、これは\(s_3\)と同じだ。
よって、\(s_5\)からプラスを読み込んだら\(s_3\)に戻る。
意味から考えても、ここの部分は数式で例えば1 + 2と来た時、後ろに+ 3が続くかどうか、といった部分になる。
そのため、ここからは同じことを繰り返し考えていくので、状態が循環するのも自然だろう。
こんな流れで状態遷移図を書くと、以下のようになる。
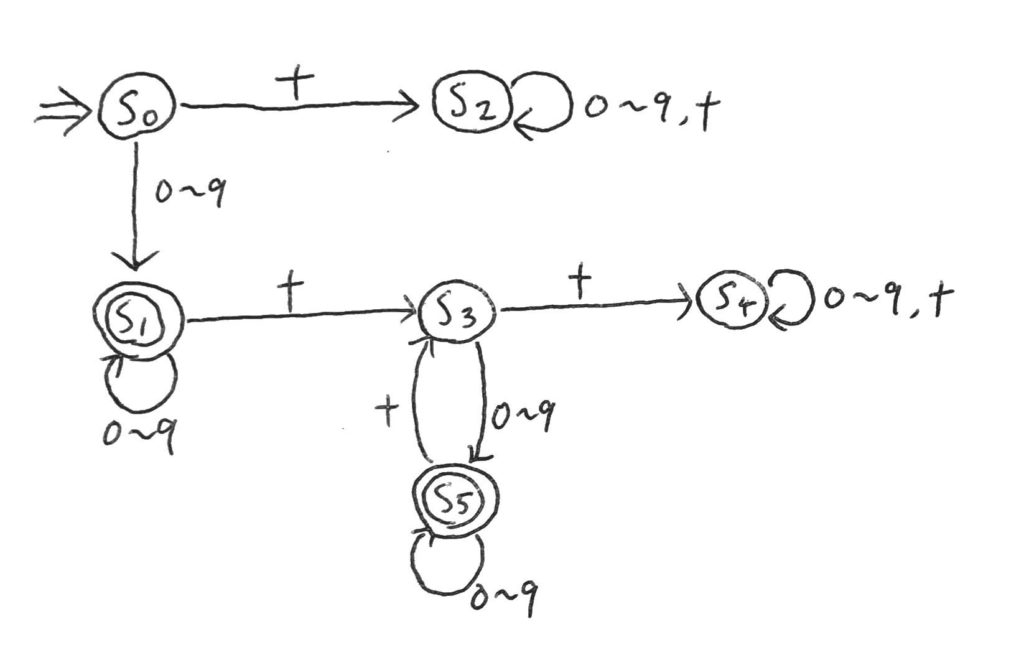
補足で、入力が空列\(\varepsilon\)の場合はNGとしている。
もしそれをOKとする場合は、\(F\)に\(s_0\)も追加してあげればいい。
この有限オートマトン\(M = (K, \Sigma, \delta, s_0, F)\)について、\(K\)、\(F\)は以下の通りだ。
- \(K = \{s_0, s_1, s_2, s_3, s_4, s_5\}\)
- \(F = \{s_1, s_5\}\)
また、状態遷移関数\(\delta\)をまとめると以下の通り。
| 現状態\(s\) | 入力\(a\) | 次状態\(\delta(s, a)\) |
|---|---|---|
| \(s_0\) | 0~9 | \(s_1\) |
| \(s_0\) | + | \(s_2\) |
| \(s_1\) | 0~9 | \(s_1\) |
| \(s_1\) | + | \(s_3\) |
| \(s_2\) | 0~9 | \(s_2\) |
| \(s_2\) | + | \(s_2\) |
| \(s_3\) | 0~9 | \(s_5\) |
| \(s_3\) | + | \(s_4\) |
| \(s_4\) | 0~9 | \(s_4\) |
| \(s_4\) | + | \(s_4\) |
| \(s_5\) | 0~9 | \(s_5\) |
| \(s_5\) | + | \(s_3\) |
これで加算だけ定義された数式は表現できた。
…のだが、無駄なことをしていることが分かるだろうか。
例えば、状態\(s_2\)、\(s_4\)に注目すると、これは両方とも何を読み込んでもアウトな状態。
ということは、同じ状態を表しているので一つにまとめてしまっても問題ないだろう。
このように、有限オートマトンを考えると二つの状態が同じことを表している部分が出てくる。
そして、この\(M\)には、実は他にもこのような状態の組が存在する。
上のようにぱっと見で分かるものであればいいが、他の組は見つけられるだろうか。
そもそも、こういった状態は実際どうなっているのか。
どうやって見つけて、削除すればいいのか。
そのあたりを、次回見ていこう。
おわりに
今回は、有限オートマトンの定義を解説した。
恐らく、これまで扱ったことのない内容だったと思う。
しかし、それぞれ何を表しているか、何をすればいいか一個一個見ていけばそんなに難しくない。
不安になったら、随時確認しながら進めていこう。
次回は、本文中にも書いた通り、同じことを意味する状態について書いていく…のだが、その時に使える直積オートマトンというものがあるので、そこから解説しよう。
当然のごとく、今回の内容をガンガン使うので、ある程度理解してから進めていきたい。
2020/11/30追記
次回の内容を投稿した。
上に書いた通り、直積オートマトンと状態の等価、そしてそれらに関する定理を3つほど紹介している。
記事の長さがかなり長いが、最悪証明はすっ飛ばしてもいいので、それぞれ何を言っているかは理解しておこう。
オマケ:例で出した有限オートマトンが認識する言語
オマケで、有限オートマトンの例で出したものが、どんな言語を認識するかを見てみよう。
状態遷移図を再掲しておく。

数式で書いたものも再掲しておこう。
この有限オートマトン\(M = (K, \Sigma, \delta, s_0, F)\)について、各集合は以下の通り。
- \(K = \{s_0, s_1, s_2, s_3\}\)
- \(\Sigma = \{0, 1\}\)
- \(F = \{s_0\}\)
また、状態遷移関数\(\delta\)は以下の表で定義されている。
| 現状態\(s\) | 入力\(a\) | 次状態\(\delta(s, a)\) |
|---|---|---|
| \(s_0\) | 0 | \(s_1\) |
| \(s_0\) | 1 | \(s_2\) |
| \(s_1\) | 0 | \(s_0\) |
| \(s_1\) | 1 | \(s_3\) |
| \(s_2\) | 0 | \(s_3\) |
| \(s_2\) | 1 | \(s_0\) |
| \(s_3\) | 0 | \(s_2\) |
| \(s_3\) | 1 | \(s_1\) |
では、これが認識する言語\(L(M)\)を見ていく…のだが。
勘のいい方ならもうお気づきかもしれない。
この言語\(L(M)\)は、0と1がそれぞれ偶数個であるような列で構成される。
これを数式で表現するために、表記を定義しよう。
ある列\(x \in \Sigma^*\)に含まれる記号\(a \in \Sigma\)の個数を\(\sharp_a(x)\)と定義する。
例えば、\(x = 011\)、\(a = 1\)のとき、\(\sharp_1(011) = 2\)だ。
これで、言語\(L(M)\)を数式で表現できる。
$$L(M) = \{x \in \Sigma^* | \sharp_a(x) = 2n, n \in \mathbb{N} \cup \{0\}, a \in \Sigma\}$$
では、これを証明していこう。
…が、直接証明するのではなく、まずは各状態がどんな状態かを説明し、それが正しいことを証明していこう。
今回の各状態は、入力列\(x\)を読み終えた後、以下の条件で遷移する。
言い換えると、\(\delta(s_0, x)\)の結果は、以下の条件で決定できる。
- \(s_0\) : \(\sharp_0(x)\)が偶数、\(\sharp_1(x)\)が偶数
- \(s_1\) : \(\sharp_0(x)\)が奇数、\(\sharp_1(x)\)が偶数
- \(s_2\) : \(\sharp_0(x)\)が偶数、\(\sharp_1(x)\)が奇数
- \(s_3\) : \(\sharp_0(x)\)が奇数、\(\sharp_1(x)\)が奇数
これが正しいことが証明できれば、\(s_0\)のみ受理状態なので明らかに命題を満たすだろう。
というわけで、これを証明していく。
方針としては、数学的帰納法だ。
まず、長さ0の列\(\varepsilon\)について命題が成立することを示す。
長さ0ということは各記号も0個、つまり偶数だ。
そして、状態は遷移しないので\(s_0\)、よって成立だ。
次に、列\(x \in \Sigma^*\)について命題が成立していると仮定する。
この後ろに記号\(a \in \Sigma\)を足し、列\(xa\)を読んでも成立するかを確認する。
これは、\(x\)を読んだ際のパターンと、\(a\)が0か1かの組合せしかないので、全パターン確認してしまおう。
まず、\(x\)を読み終えた時点で、状態が\(s_0\)だったとする。
このとき、帰納法の仮定から\(x\)内の0, 1の個数はそれぞれ偶数だ。
ここに、記号\(a\)を読み込ませる。
- \(\delta(s_0, 0) = s_1\)
- \(\delta(s_0, 1) = s_2\)
\(a = 0\)のとき、列\(xa\)は状態\(s_1\)に遷移する。
この中の0の個数は偶数に1増えるので奇数、1の個数は変わらないので偶数。
これは\(s_1\)の条件に当てはまっているので問題ない。
\(a = 1\)のときは、列\(xa\)は\(s_2\)に遷移する。
個数を見ると、0は変わらないので偶数、1は偶数から1個だけ増えてるので奇数。
\(s_2\)の条件と合致したので大丈夫だ。
こんな感じで確認していくと、以下の表のようになる。
| \(\delta(s_0, x)\) | \(\sharp_0(x)\) | \(\sharp_1(x)\) | \(a\) | \(\delta(s_0, xa)\) | \(\sharp_0(xa)\) | \(\sharp_1(xa)\) |
|---|---|---|---|---|---|---|
| \(s_0\) | 偶数 | 偶数 | 0 | \(s_1\) | 奇数 | 偶数 |
| \(s_0\) | 偶数 | 偶数 | 1 | \(s_2\) | 偶数 | 奇数 |
| \(s_1\) | 奇数 | 偶数 | 0 | \(s_0\) | 偶数 | 偶数 |
| \(s_1\) | 奇数 | 偶数 | 1 | \(s_3\) | 奇数 | 奇数 |
| \(s_2\) | 偶数 | 奇数 | 0 | \(s_3\) | 奇数 | 奇数 |
| \(s_2\) | 偶数 | 奇数 | 1 | \(s_0\) | 偶数 | 偶数 |
| \(s_3\) | 奇数 | 奇数 | 0 | \(s_2\) | 偶数 | 奇数 |
| \(s_3\) | 奇数 | 奇数 | 1 | \(s_1\) | 奇数 | 偶数 |
これを見てもらうと、\(xa\)の最終的な遷移先の条件と、\(xa\)内の0, 1の奇遇が綺麗に一致していることが分かる。
よって、各状態の条件が正しいことが証明できた。
上で書いた通り、受理状態は\(s_0\)のみで、この\(s_0\)は0と1の両方とも偶数個なので、命題も成立だ。



コメント