オートマトン・言語と計算理論「直積オートマトンと状態の等価性」

本シリーズでは、以下の本に沿って解説を書いている。

Amazon.co.jp

前回は、有限オートマトンを解説した。

色々と定義したが、細かい単位で見れば難しいことはないはず。

不安になったら、それが何を言っていたか、定義を見直してみよう。

以下がその記事だ。

今回は、前回のラストに書いた通り、まずは直積オートマトンを解説する。

その後、状態の等価性というものを紹介し、それらに関する定理を幾つか証明していこう。

…証明はかなり長くなりそうだが、頑張ってついてきてほしい。

直積オートマトン
1. 参考書の具体例
2. 到達不可能な状態
状態の等価性
1. 等価な状態を考える理由
等価を使った定理
おわりに
1. オマケ：さりげなく使っていた内容の証明

直積オートマトン

前回は、一つの有限オートマトンに対して解説を行った。

これに対し、複数の有限オートマトンを一つにまとめる、ということを今回解説しよう。

それが、タイトルにもある通り、直積オートマトンというもの。

これは、二つの有限オートマトンを同時に動かしているイメージだ。

例えば、一つは列内の0の個数が偶数の場合に受理し、もう一つは列内の1の個数が偶数の場合に受理する、とする。

このとき、同時に動かせば、前回の例でやったような0と1の個数がともに偶数、といった列を受理させることができるようになる。

では、定義を。

入力記号の集合$\Sigma$が等しい二つの有限オートマトンをそれぞれ$M_1 = (K_1, \Sigma, \delta_1, s_0, F_1)$、$M_2 = (K_2, \Sigma, \delta_2, t_0, F_2)$とする。

このとき、これらの直積オートマトンを$M = (K, \Sigma, \delta, (s_0, t_0), F)$とし、各内容を以下で定義する。

$K = K_1 \times K_2 = \{(s, t) | s \in K_1, t \in K_2\}$
$\delta : K \times \Sigma \rightarrow K$
$F \subset K$

ちょっと補足をしていこう。

まず、状態の集合$K$は、元の二つの有限オートマトンそれぞれの状態の組になっている。

次に、状態遷移関数$\delta$だが、$s \in K_1$、$t \in K_2$、$a \in \Sigma$として以下のようになっている。

$$\delta((s, t), a) = (\delta_1(s, a), \delta_2(t, a))$$

要するに、組になっているそれぞれの状態に対し、記号$a$で遷移させたものの組が直積オートマトン上での状態遷移となる。

この定義にするため、入力記号$\Sigma$は一致している必要があるのだ。

最後、ここが注意点なのだが、受理状態の集合$F$は条件によって異なる。

例えば、上で出したように、元の有限オートマトンの両方で受理されるものとすれば、この$F$は…

$$F = \{(s, t) \in K | s \in F_1 かつ t \in F_2\}$$

となる。

また、どちらかのみでも受理されればOKの場合は、上の「かつ」が「または」になる。

このように、何がしたいかによって受理状態は変化するので、そこに気を付けよう。

参考書の具体例

では、実際にこの直積オートマトンを作ってみよう。

ここでは、参考書に載っている例をそのまま引用させてもらう。

受理状態は、元の両方ともが認識するものとする。

先に、直積させる二つの有限オートマトンを紹介しよう。

入力記号はともに同じで、$\Sigma = \{0, 1\}$だ。

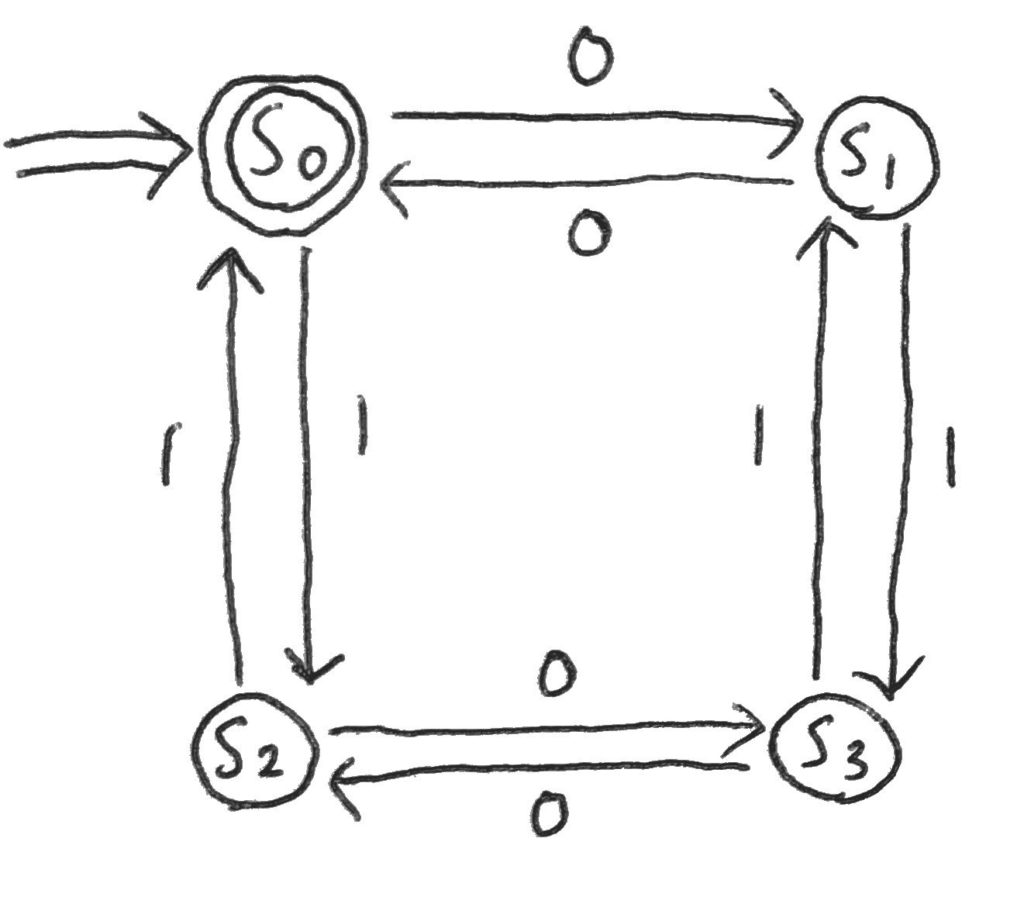
有限オートマトン$M_1$

一つ目は、任意の列$x \in \Sigma^*$について、その0の個数と1の個数がともに偶数であるような列を受理する。

これは前回出した例そのままだ。

状態遷移図だけ再掲するので、詳細は前回の記事を参照してほしい。

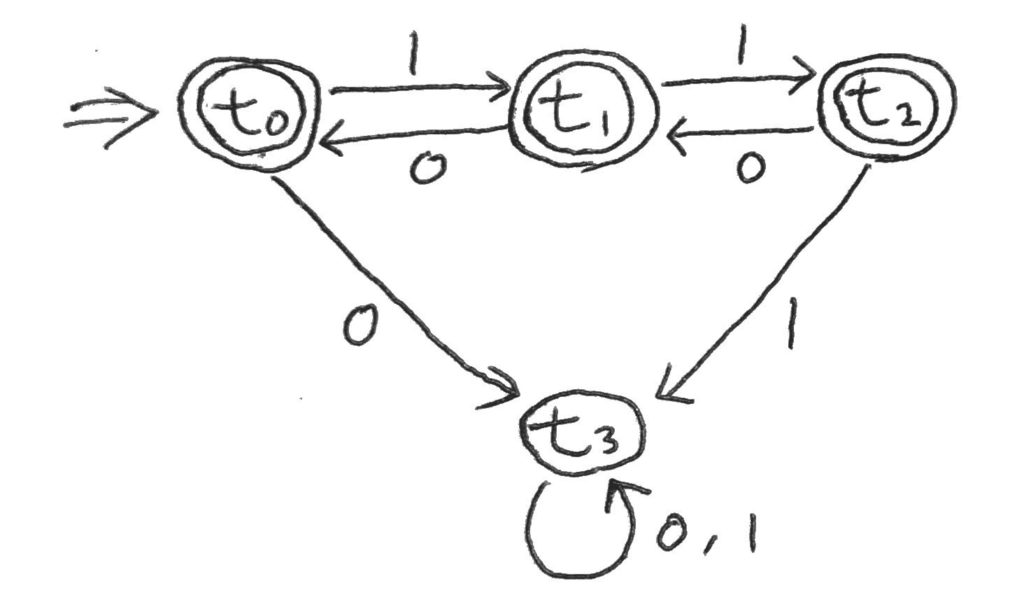
有限オートマトン$M_2$

二つ目は、任意の列$x \in \Sigma^*$について、先頭から0と1の個数をカウントしていく。

その時、1の個数から0の個数を引いたものが常に0以上2以下であるような列を受理する、というもの。

なお、ある列$x$について$x = yy’$と書けるとき、この$y$を$x$のプレフィックスと呼ぶ。

これを使うと、言語$L(M_2)$は以下のように表記できる。

$$L(M_2) = \{x \in \Sigma^* | 0 \leq \sharp_1(y) – \sharp_0(y) \leq 2, yはxのプレフィックス\}$$

ここから有限オートマトンを作る部分まで解説すると非常に長くなってしまうので、ここでは結果の状態遷移図だけ載せよう。

余力があれば、これを作ってみてほしい。

直積オートマトン

では、これらの直積オートマトンを考えていこう。

まず状態だが、定義は以下の通りだった。

$$K = K_1 \times K_2 = \{(s, t) | s \in K_1, t \in K_2\}$$

これに当てはめると、以下のようになっていることが分かる。

$$\begin{eqnarray}
K = & \{ & (s_0, t_0), (s_0, t_1), (s_0, t_2), (s_0, t_3), \\
& & (s_1, t_0), (s_1, t_1), (s_1, t_2), (s_1, t_3), \\
& & (s_2, t_0), (s_2, t_1), (s_2, t_2), (s_2, t_3), \\
& & (s_3, t_0), (s_3, t_1), (s_3, t_2), (s_3, t_3) \}
\end{eqnarray}$$

ちょっと数が多いが、めげずに進めよう。

次に状態遷移関数を考えるが、幾つか具体例を挙げるにとどめよう。

でないと、全部で32個のパターンになってしまうので、~~さすがにつらい~~見づらくなってしまうだろう。

例えば、状態$(s_0, t_0)$から順番に1, 1, 0と読んでみる。

$\delta((s_0, t_0), 1) = (\delta_1(s_0, 1), \delta_2(t_0, 1)) = (s_2, t_1)$
$\delta((s_2, t_1), 1) = (\delta_1(s_2, 1), \delta_2(t_1, 1)) = (s_0, t_2)$
$\delta((s_0, t_2), 0) = (\delta_1(s_0, 0), \delta_2(t_2, 0)) = (s_1, t_1)$

こんな感じだ。

そして、受理状態$F$について、今回は両方とも受理状態になっているものなので…

$$\begin{eqnarray}
F & = & \{(s, t) \in K | s \in F_1, t \in F_2\} \\
& = & \{(s_0, t_0), (s_0, t_1), (s_0, t_2)\}
\end{eqnarray}$$

の三つが該当する。

これらをもとに、この直積オートマトンの状態遷移図を…頑張って書いてみた。

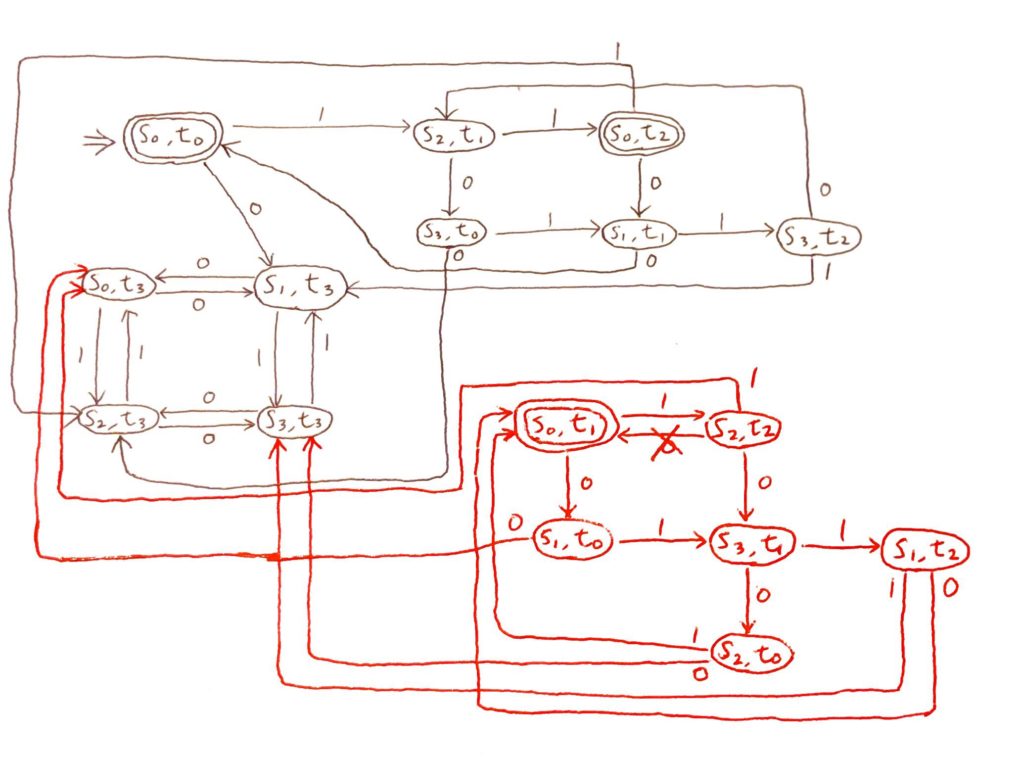
赤い部分については、後で解説する。

一か所だけ、参考書で間違っている部分があったので補足をしておこう。

状態$(s_2, t_2)$から、0による遷移が2本書かれていた。

そのうち、$(s_0, t_2)$に向かう遷移は誤りで、正しいのは$(s_3, t_1)$への遷移のみだ。

上の図でも×印で消してあるので、そこだけ注意。

というわけで、これが直積オートマトンだ。

到達不可能な状態

さて、上の直積オートマトン$M$で、赤くしたところに注目しよう。

ここの部分なのだが、実は初期状態$(s_0, t_0)$からはどう頑張っても到達することができない。

そういった状態を考えるのは明らかに無駄だろう。

ということで、今後はこういった部分は省いて考える。

つまり、上の直積オートマトンについても、そこを省いて以下のような状態遷移図として考えていくことにする。

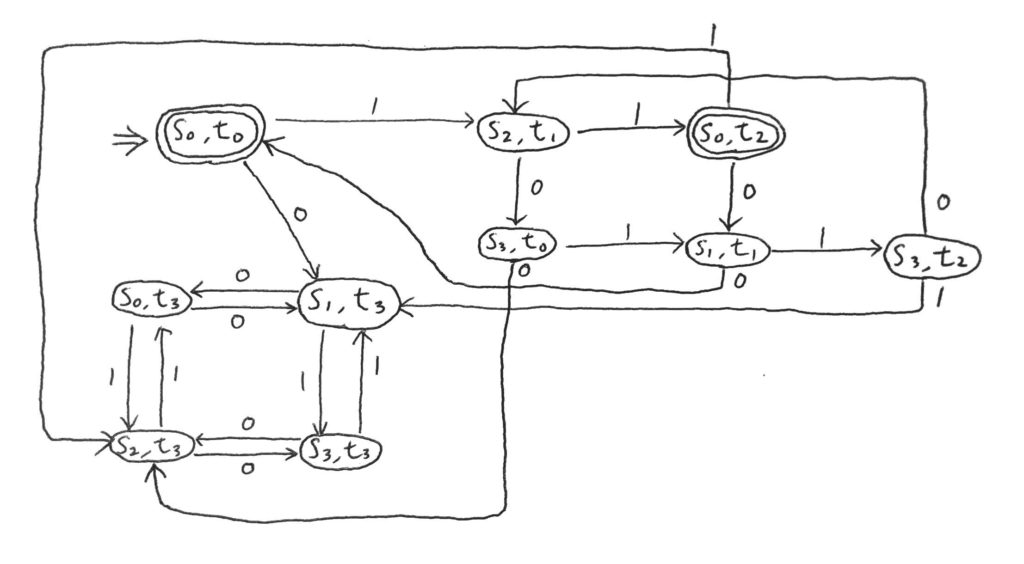
このことを考えると、直積オートマトンの状態$K$の定義を少し変えた方がいいだろう。

先に状態遷移関数$\delta$が定義されているとし、状態$K$は以下のように定義できる。

$$K = \{\delta((s_0, t_0), x) | x \in \Sigma^*\} \subset K \times K$$

これは、初期状態$(s_0, t_0)$から列$x \in \Sigma^*$で遷移できる状態の集合だ。

状態の等価性

さて、ここから話は再度一つの有限オートマトン$M$に戻る。

ここから、今回のメインである状態の等価性というものを解説していこう。

前回の本編最後にお見せした、加算のみの数式を認識する有限オートマトンで、同じことを表現する状態が複数存在する、ということを書いたと思う。

もうちょっと詳しく書くと、二つの状態$s_1, s_2 \in K$からどんな列を読んでも、その結果受理状態になるかどうかが一致している、ということだ。

このとき、その二つの状態のことを等価であるという。

これも、数式で定義してしまおう。

有限オートマトン$M = (K, \Sigma, \delta, s_0, F)$内の二つの状態$s_1, s_2 \in K$に注目する。

任意の列$x \in \Sigma^*$について以下が成り立っているとき、$s_1, s_2$は等価であるといい、$s_1 \equiv s_2$と表記する。

$$\delta(s_1, x) \in F \Leftrightarrow \delta(s_2, x) \in F$$

どういうことか、具体例で見てみよう。

数式の状態遷移図を再掲してみる。

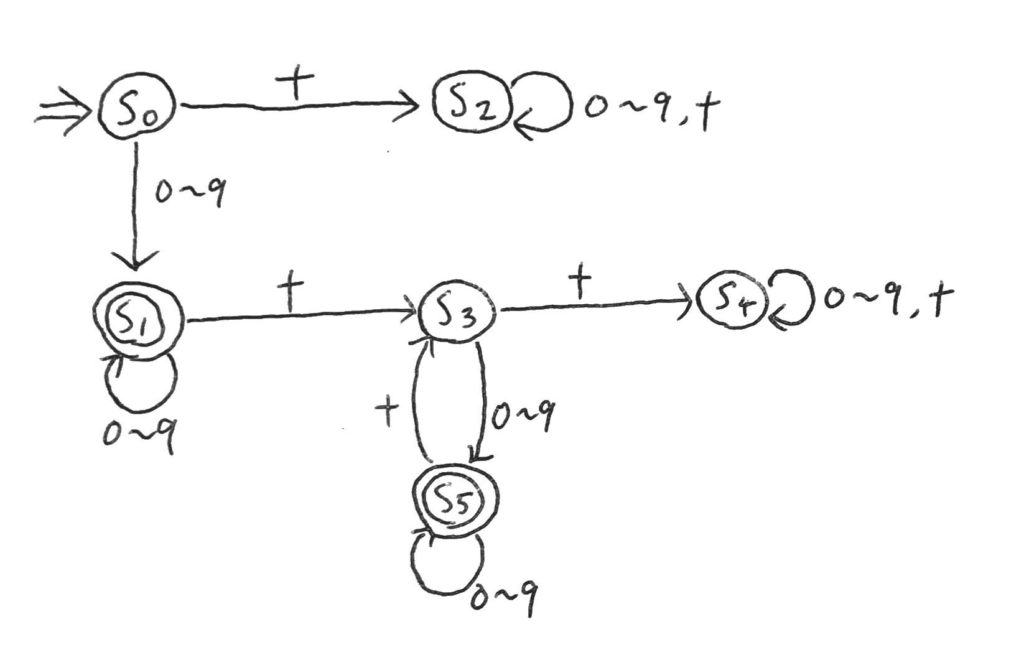
これについて、$s_2$と$s_4$はそこからどんな記号を読んでも自身に遷移し、受理しないことが分かる。

つまり、任意の列$x \in \Sigma^*$について…

$$\delta(s_2, x) \not \in F かつ \delta(s_4, x) \not \in F$$

が成り立っている。

この二つの状態が等価であるための条件は、$x \in \Sigma^*$を任意の列として…

$$\delta(s_2, x) \in F \Leftrightarrow \delta(s_4, x) \in F$$

となってこれは成り立っているので、この二つは等価、$s_2 \equiv s4$となるのだ。

等価な状態を考える理由

等価の定理に入る前に、これを少し考えてみよう。

なぜ、こういった等価な状態を考える必要があるのか、という部分だ。

最終的には、こういったオートマトンをプログラムで組んで、実際に文字列を判定することになる。

その際、この状態の数だけ容量が多く必要になってしまうのだ。

そのため、できるだけ状態数は少ない方が効率が良くなる。

そして、この後解説するのだが、こういった等価な状態というのは、まとめて1つの状態にすることができる。

この状態数の削減ができるかどうかの判定、できるならどこを削減するかの探索に使えるから、等価を考えているのだ。

等価を使った定理

では、等価な状態が絡んだ定理を幾つかご紹介…の前に、証明や操作などで使いたい記号があるので、先に定義してしまおう。

等価な状態を一つの集合にまとめる記号だ。

有限オートマトン$M = (K, \Sigma, \delta, s_0, F)$内で、ある状態$s \in K$に注目する。

このとき、$s$と等価な状態の集合を、$[s]$と表記する。

$$[s] = \{s’ \in K | s \equiv s’\}$$

一つ注意として、$s \equiv s$はどんな状態にも成り立つので、必ず$s \in [s]$だ。

これを踏まえた上で、定理を見ていこう。

定理1：等価な状態とより少ない状態数の有限オートマトン

一つ目は、以下のような定理だ。

二つの有限オートマトン$M$について、等価な2状態が存在すれば、同じ言語を認識し、状態数が$M$より1個少ない有限オートマトン$M’$が存在する。

これが証明できれば、等価な2状態が存在したとき、同じ言語を認識するより状態数が少ない有限オートマトンを作ることができるのだ。

では、証明していく。

方針としては、実際に$M$からそれよりも状態数が少ない有限オートマトン$M’$を作り、それらが同じ言語を認識することを示す。

早速$M’$を作っていこう。

元の有限オートマトンを$M = (K, \Sigma, \delta, s_0, F)$とし、新たに$M’ = (K’, \Sigma, \delta’, s’_0, F’)$を作る。

このとき、$M’$の各要素は以下のように定義する。

$K’ = \{[s] | s \in K\}$
$\delta'([s], a) = [\delta(s, a)]$　※$a \in \Sigma$
$s’_0 = [s_0]$
$F’ = \{[s] | s \in F\}$

どうやって$M’$を作るか、言葉でも説明しておこう。

元の有限オートマトン$M$に対し、以下の手順を行うことで$M’$を作る。

ある状態$s$と等価な状態$s_1, s_2, …, s_n$をひとまとめにし、それを新たな一つの状態$[s]$とする
$s_1, s_2, …, s_n$への遷移があった場合に、その遷移先を$[s]$に変更する

このとき、$M’$の方が状態数が少ないことは明らかだろう。

では、$M$と$M’$が同じ言語を認識することを証明していく…前に、一つ気になる部分がある。

$M’$の状態遷移関数$\delta’$は上の定義で問題ないのだろうか。

操作では、等価な状態に向かう遷移に関して操作を行っていた。

確かに、向かう元から等価な状態への遷移は大丈夫なのだが、そこから先はこの定義に変えていいのだろうか。

例えば、今$s_1, s_2 \in K$が等価で、$\delta(s_1, a) = s_3$、$\delta(s_2, a) = s_4$だったとしよう。

上の定義によると、$\delta'([s_1], a) = [\delta(s_1, a)] = [s_3]$となり、$\delta'([s_2], a) = [\delta(s_2, a)] = [s_4]$だと分かる。

しかし、$s_1 \equiv s_2$より$[s_1] = [s_2]$なので、$[s_3] = [s_4]$も言えてしまうのだ。

そこで、まずはこれで問題ないことを示していこう。

このためには、等価な2状態$s_1, s_2$と任意の記号$a \in \Sigma$に対して、$\delta(s_1, a) \equiv \delta(s_2, a)$が言えればいい。

なお、ここから行う証明では、記号に対する遷移$\delta$と列に対する遷移$\hat{\delta}$を分けて書いた方が分かりやすい。

そのため、本記事においてはハット記号$\hat{}$は省略せず書くこととしよう。

補題1：等価な状態からの遷移

有限オートマトン$M = (K, \Sigma, \delta, s_0, F)$内の異なる2状態$s_1, s_2 \in K$に注目する。

このとき、$s_1 \equiv s_2$ならば、任意の記号$a \in \Sigma$に対して$\delta(s_1, a) \equiv \delta(s_2, a)$が成立する。

等価な2状態に対して、同じ記号によって遷移した先も等価だ、という内容。

上に書いた通り、これが証明できれば定義に問題はない。

では、証明していこう。

まず、任意の列$x \in \Sigma^*$について、$\hat{\delta}(\delta(s_1, a), x) \in F \Leftrightarrow \hat{\delta}(s_1, ax) \in F$が成立する。

これは、$s_1$からまず記号$a$で遷移してから列$x$で遷移しているものと、列$ax$で遷移しているもので、そもそもこの二つは等しい。

次に、$\hat{\delta}(s_1, ax) \in F \Leftrightarrow \hat{\delta}(s_2, ax) \in F$が言える。

これは、前提から$s_1 \equiv s_2$なので、等価の定義から問題ない。

そして、$\hat{\delta}(s_2, ax) \in F \Leftrightarrow \hat{\delta}(\delta(s_2, a), x) \in F$が成立。

これは一つ目の変形と逆のことをしているだけなので、大丈夫だろう。

これらから、以下の内容が言えたことになる。

$$\hat{\delta}(\delta(s_1, a), x) \in F \Leftrightarrow \hat{\delta}(\delta(s_2, a), x) \in F$$

今、$\delta(s_1, a)$という状態と、$\delta(s_2, a)$という状態から同じ任意の列$x$を読んだ遷移先について、受理されるかどうかが一致している。

これは、等価の定義そのものだ。

よって、$\delta(s_1, a) \equiv \delta(s_2, a)$が証明できた。

これにより、$M’$の状態遷移関数$\delta’$に問題ないことが分かったので、先に進もう。

本題の証明に…戻る前に、もう二つほど補題を証明しておく。

これらが証明できれば、カンタンな変形だけで元の定理が証明できる。

そのための準備と思ってもらいたい。

補題2：変形前後の受理状態

今回メインで証明したい有限オートマトン$M, M’$に注目する。

このとき、$s \in F \Leftrightarrow [s] \in F’$が成立する。

早速、証明していこう。

まずは右向き矢印、$s \in F \Rightarrow [s] \in F’$を見ていこう。

前提から$s \in F$、$F’$の定義は$F’ = \{[s] | s \in F\}$だったので、もはや成り立つのは自明だろう。

次に、左向き矢印、(前提)⇒(結論)に直して$[s] \in F’ \Rightarrow s \in F$を見ていく。

ここで、$[s] = \{s_1, s_2, …, s_n\}$と具体的に置いて、任意の$s_i \in [s]$について$s_i \in F$となることを示す。

$F’$の定義から、とりあえずある$j$について$s_j \in F$が成り立つ。

また、$s_j$は$s$と等価な状態のうちの一つなので、$s_j \in [s] = \{s_0, s_1, …, s_n\}$が言える。

このとき、$s_i \in [s]$から$s_i \equiv s_j$なので、任意の列$x \in \Sigma^*$について以下が成立する。

$$\hat{\delta}(s_i, x) \in F \Leftrightarrow \hat{\delta}(s_j, x) \in F$$

さて、$x$は任意の列なので、空列$\varepsilon$でも大丈夫だ。

これを入れてみると…

$$\hat{\delta}(s_i, \varepsilon) = s_i \in F \Leftrightarrow \hat{\delta}(s_j, \varepsilon) = s_j \in F$$

が言えた。

さて、さっき$s_j \in F$と分かっていたので、左向きに見て$s_i \in F$となり、これも成立だ。

よって、$s \in F \Leftrightarrow [s] \in F’$が証明できた。

補題3：列に対する遷移

今回メインで証明したい有限オートマトン$M, M’$に注目する。

このとき、どんな状態$s \in K$に対しても、任意の列$x \in \Sigma^*$について以下が成立する。

$$\hat{\delta’}([s], x) = [\hat{\delta}(s, x)]$$

定義では記号に対する遷移だったが、列に拡張できる、ということを言っている。

これは、列$x$の長さに関する帰納法で証明しよう。

まず、$|x| = 0$…つまり、$x = \varepsilon$の場合。

左辺は$\hat{\delta’}([s], \varepsilon) = [s]$。

右辺は$[\hat{\delta}(s, \varepsilon)] = [s]$。

よって、問題ない。

次に、列$x$に対して成立していると仮定し、その前に記号$a \in \Sigma$を足して$ax$について見てみよう。

左辺から変形していき、最終的に右辺の形まで持っていく。

まず、$\hat{\delta’}([s], ax) = \hat{\delta’}(\delta'([s], a), x)$、これはさっきもやった遷移の分解だ。

次に、$\hat{\delta’}(\delta'([s], a), x) = \hat{\delta’}([\delta(s, a)], x)$、これは$\delta’$の定義を使っての変形だ。

そして、$\hat{\delta’}([\delta(s, a)], x) = [\hat{\delta}(\delta(s, a), x)]$、ちょっと分かりづらいかもしれないが、これは帰納法の仮定から言える。

最後に、分けていた遷移をひとまとめにして$[\hat{\delta}(\delta(s, a), x)] = [\hat{\delta}(s, ax)]$。

これで、全部繋げると$\hat{\delta’}([s], ax) = [\hat{\delta}(s, ax)]$となったので、成立だ。

メインの証明

ここまできて、ようやくメインとなる内容の証明だ。

ちょっと間が空いてしまったので、証明する内容を再掲しておこう。

元の有限オートマトンを$M = (K, \Sigma, \delta, s_0, F)$とし、新たに$M’ = (K’, \Sigma, \delta’, s’_0, F’)$を作る。

このとき、$M’$の各要素は以下のように定義する。

$K’ = \{[s] | s \in K\}$
$\delta'([s], a) = [\delta(s, a)]$　※$a \in \Sigma$
$s’_0 = [s_0]$
$F’ = \{[s] | s \in F\}$

これで、$M$と$M’$が同じ言語を認識することを示せばよかった。

同じ言語を認識する、というのは任意の列$x \in \Sigma^*$について、

$$x \in L(M) \Leftrightarrow x \in L(M’)$$

が言えればいい。

ということで、順番に見ていこう。

左側から出発し、同値を繋げて右側に持っていく。

まず、受理の定義から$x \in L(M) \Leftrightarrow \hat{\delta}(s_0, x) \in F$が成立する。

次に、補題2から$\hat{\delta}(s_0, x) \in F \Leftrightarrow [\hat{\delta}(s_0, x)] \in F’$。

補題3から$[\hat{\delta}(s_0, x)] = \hat{\delta’}([s_0], x)$なので、$[\hat{\delta}(s_0, x)] \in F’ \Leftrightarrow \hat{\delta’}([s_0], x) \in F’$。

そして、$[s_0] = s’_0$なので、$\hat{\delta’}([s_0], x) \in F’ \Leftrightarrow \hat{\delta’}(s’_0, x) \in F’$。

列が受理されることの定義から、$\hat{\delta’}(s’_0, x) \in F’ \Leftrightarrow x \in L(M’)$。

以上から、同値条件を繋げていけば$x \in L(M) \Leftrightarrow x \in L(M’)$なので、成立だ。

長くなってしまったが、これで等価な状態を含む有限オートマトンに対し、それよりも少ない状態数にできることと、その方法が証明できたことになる。

定理2：定理1の逆

実は、定理1の逆も成り立つ。

ある有限オートマトン$M$と同じ言語を認識し、かつ状態数が少ない別の有限オートマトン$M’$が存在したとする。

このとき、$M$内には等価な2状態が必ず存在する、という内容だ。

そんなに難しくないので、サクッと証明してしまおう。

これには背理法を使う。

同じ言語を認識する二つの有限オートマトン$M, M’$について、$|K| = n > |K’|$としよう。

このとき、$M$内の任意の2状態$s_1, s_2 \in K$について$s_1 \not \equiv s_2$と仮定しておく。

まず、$M$内の各状態に遷移するような列$x$を列挙する。

どういうことかというと、$\hat{\delta}(s_0, x_0) = s_0, \hat{\delta}(s_0, x_1) = s_1, …$といった感じで列$x_0, x_1, …, x_n$を決めてしまう。

このとき、どの2状態も等価ではないので、列挙した列の中身は全て異なっている。

次に、この列挙した列を全て$M’$に読み込ませてみよう。

このとき、鳩ノ巣原理から、必ず同じ状態に遷移する二つの列$x_i, x_j$が存在する。

前提で$n > |K’|$と置いており、$n$個の列を鳩、$n$より少ない数の状態を巣箱と見なせばいい。

ここで、$M$内では$\hat{\delta}(s_0, x_i) = s_i$、$\hat{\delta}(s_0, x_j) = s_j$となり、$M’$内では$\hat{\delta’}(s’_0, x_i) = \hat{\delta’}(s’_0, x_j) = s’_k$になったとしよう。

背理法の仮定から、$s_i \not \equiv s_j$が使える。

ここから、$\hat{\delta}(s_i, y) \in F$かつ$\hat{\delta}(s_j, y) \not \in F$となる列$y$が存在することがわかる。

本当はこの受理・非受理を入れ替えたパターンもあるのだが、文字を置き換えれば同じ議論で進められるのでこう置いておこう。

このとき、$M$に対しては列$x_iy$は受理され、列$x_jy$は受理されない。

今度は$M’$で見てみよう。

列$x_iy, x_jy$をそれぞれ入力すると、以下のようになる。

$\hat{\delta’}(s’_0, x_iy) = \hat{\delta’}(\hat{\delta’}(s’_0, x_i), y) = \hat{\delta’}(s’_k, y)$
$\hat{\delta’}(s’_0, x_jy) = \hat{\delta’}(\hat{\delta’}(s’_0, x_j), y) = \hat{\delta’}(s’_k, y)$

ということで、まったく同じ先に遷移する。

つまり…

$$x_iy \in L(M’) \Leftrightarrow x_jy \in L(M’)$$

が言えたことになる。

さて、$M$では列$x_iy, x_jy$はどちらかが受理され、どちらかが受理されなかった。

それに対し、$M’$は両方とも受理される、あるいはされないのどちらか。

これでは認識する言語が変わってしまうので、矛盾だ。

よって、仮定で置いた等価な状態が存在しない、というのが間違っていることがわかった。

以上から、成立だ。

ちょっとオマケで、この定理が成り立つと何が嬉しいかを紹介しておこう。

定理の対偶を取ると、以下のようになる。

ある有限オートマトン$M$内のどの2状態も等価でないならば、それよりも状態数が少なく、同じ言語を認識する有限オートマトン$M’$は存在しない。

言い換えると、どの2状態も等価でないなら、その有限オートマトン$M$は、同じ言語を認識する物の中で状態数が最小である、となるのだ。

このことから、等価な状態を探し、それを定理1の方法で削減していくだけで、同じ言語を認識する最小の有限オートマトンが得られるのだ。

本では紹介されていないが、この最小の有限オートマトンのことを既約と呼ぶらしい。

定理3：等価な2状態を見つける方法

ここまでは、等価な2状態があればより小さくできることと、逆に等価な2状態が無ければそれが最小であることを示してきた。

今度は、その2状態を見つける方法に使える定理だ。

やることが複雑になるので、丁寧に進めよう。

まず、有限オートマトン$M$内の2状態$s_i, s_j \in K$が等価か調べたいとする。

このとき、以下の手順で$M$と$M$直積オートマトン$M’$を作る。

初期状態を$(s_i, s_j)$とする。
状態遷移関数は通常の直積オートマトンの定義に従って定義する。
状態$K$は、初期状態から辿れるもののみとする。
受理状態は使用しないので$F’ \subset K$と置き、中身は定義しない。

初期状態が重要な意味を持つので、この$M’$を$M[s_i, s_j]$と表記することにしよう。

ただし、この表記だけは本記事のみで使用しているものなので、そこだけ注意。

つまり、この$M[s_i, s_j] = (K’, \Sigma, \delta’, (s_i, s_j), F’)$は…

$K’ = \{\delta'((s_i, s_j), x) \in K \times K | x \in \Sigma^*\}$
$\delta'((s_k, s_l), a) = (\delta(s_k, a), \delta(s_l, a))$　※$s_k, s_l \in K, a \in \Sigma$
$F’ \subset K’$

こんな形になっている。

ここで、以下のような状態の部分集合$D \subset K’$を考える。

$$D = \{(s_k, s_l) \in K’ | s_k \in F \Leftrightarrow s_l \in F\}$$

要するに、元の有限オートマトン$M$内のある2状態$s_k, s_l \in K$について、受理状態かどうかが一致していれば、$M’$内の状態$(s_k, s_l)$を$D$に含める。

このとき、以下が成立する。

$$s_i \equiv s_j \Leftrightarrow K’ = D$$

日本語で書けば、$s_i$と$s_j$が等価であることと、$M[s_i, s_j]$内の任意の状態$(s_k, s_l) \in K’$について、$s_k, s_l \in F$か$s_k, s_l \not \in F$となることが同じだと言っている。

これでもちょっと分かりづらいが、これを証明した後に、実際に見つける流れを例題としてやってみるので、そこで理解してほしい。

ということで、まずは証明だ。

先に右向き矢印、$s_i \equiv s_j \Rightarrow K’ = D$を見ていくのだが、今回は集合のイコールだ。

このとき、通常は$K’ \subset D$かつ$D \subset K’$を示すのだが、$D$の定義から$D \subset K’$はすでに言えている。

つまり、$K’ \subset D$が示せればよい。

これをさらに言い換えて、$(s_k, s_l) \in K’ \Rightarrow (s_k, s_l) \in D$を示す。

さて、最初に$K’$の定義を少し書き換えよう。

$$K’ = \{(\delta(s_i, x), \delta(s_j, x)) \in K \times K | x \in \Sigma^*\}$$

$\delta’$の定義に従って書き換えただけだ。

これにより、任意の列$x \in \Sigma^*$に対し、$(\delta(s_i, x), \delta(s_j, x)) \in D$を言えばいい、ということになる。

前提から$s_i \equiv s_j$だったので、$\delta(s_i, x) \in F \Leftrightarrow \delta(s_j, x) \in F$だ。

これが$D$の条件なので、$(\delta(s_i, x), \delta(s_j, x)) \in D$は成り立つ。

これで右向きはOKだ。

次に左向き、$K’ = D \Rightarrow s_i \equiv s_j$を示そう。

まず、$K’$の定義から、任意の列$x$に対して、$(\delta(s_i, x), \delta(s_j, x)) \in K’$。

$K’ = D$、$D$の定義から、$\delta(s_i, x) \in F \Leftrightarrow \delta(s_j, x) \in F$が言える。

これは等価の定義なので、$s_i \equiv s_j$、よってこちらも成立だ。

両向きともいえたので、定理が証明できた。

実際に状態を減らしてみた

最後に、ここまでの内容を使って実際に状態を削減してみよう。

具体例として、前回作った加算のみの数式を受理する有限オートマトンでやってみる。

状態遷移図を再掲しよう。

数式でも書いておくと、$M = (K, \Sigma, \delta, s_0, F)$として…

$K = \{s_0, s_1, s_2, s_3, s_4, s_5\}$
$\Sigma = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +\}$
$F = \{s_1, s_5\}$

また、状態遷移関数$\delta$の内訳を以下の表に示しておく。

現状態$s$	入力$a$	次状態$\delta(s, a)$
$s_0$	0～9	$s_1$
$s_0$	+	$s_2$
$s_1$	0～9	$s_1$
$s_1$	+	$s_3$
$s_2$	0～9	$s_2$
$s_2$	+	$s_2$
$s_3$	0～9	$s_5$
$s_3$	+	$s_4$
$s_4$	0～9	$s_4$
$s_4$	+	$s_4$
$s_5$	0～9	$s_5$
$s_5$	+	$s_3$

$M$における状態遷移関数$\delta$

これで、実際に見ていく…前に、方針をまとめよう。

まず、全ての2状態$s_i, s_j \in K$を初期状態とする直積オートマトン$M[s_i, s_j]$を作る。

このとき、同じ状態の組は必ず等価になるので、考える必要はないだろう。

また、二つの順番を入れ替えたものは明らかに同じ結果になるので、片方の組合せだけ見ればいい。

次に、$M[s_i, s_j]$内の全ての状態$(s_k, s_l) \in K’$について、$s_k, s_l$がそれぞれ$M$における受理状態かどうかを見よう。

これが、全て$s_k \in F, s_l \in F$もしくは$s_k \not \in F, s_l \not \in F$となっていれば、$s_i \equiv s_j$なので、まとめて$[s_i]$として縮小する。

逆に、一つでも$s_k \in F, s_l \not \in F$もしくは$s_k \not \in F, s_l \in F$となっているものがあれば、その時点で$s_i \not \equiv s_j$と分かるので、この時は何もしない。

これを繰り返し見ていく、という感じになる。

ということで、今回の場合は以下の組合せだけ直積オートマトンを作ればいい。

$M[s_0, s_1]$
$M[s_0, s_2]$
$M[s_0, s_3]$
$M[s_0, s_4]$
$M[s_0, s_5]$
$M[s_1, s_2]$
$M[s_1, s_3]$
$M[s_1, s_4]$
$M[s_1, s_5]$
$M[s_2, s_3]$
$M[s_2, s_4]$
$M[s_2, s_5]$
$M[s_3, s_4]$
$M[s_3, s_5]$
$M[s_4, s_5]$

…計15個。

さすがに手で全て計算するには骨が折れるので、今回は一つだけ試しにやってその後最終形をお見せし、残りの計算は別記事でプログラムを組んでしまおう。

これまで出していなかった$s_1, s_5$に注目する。

ネタ晴らしをしてしまうと、これが隠れた等価な状態の組の一つだ。

有限オートマトン$M[s_1, s_5]$を作った結果の状態遷移図を以下に示そう。

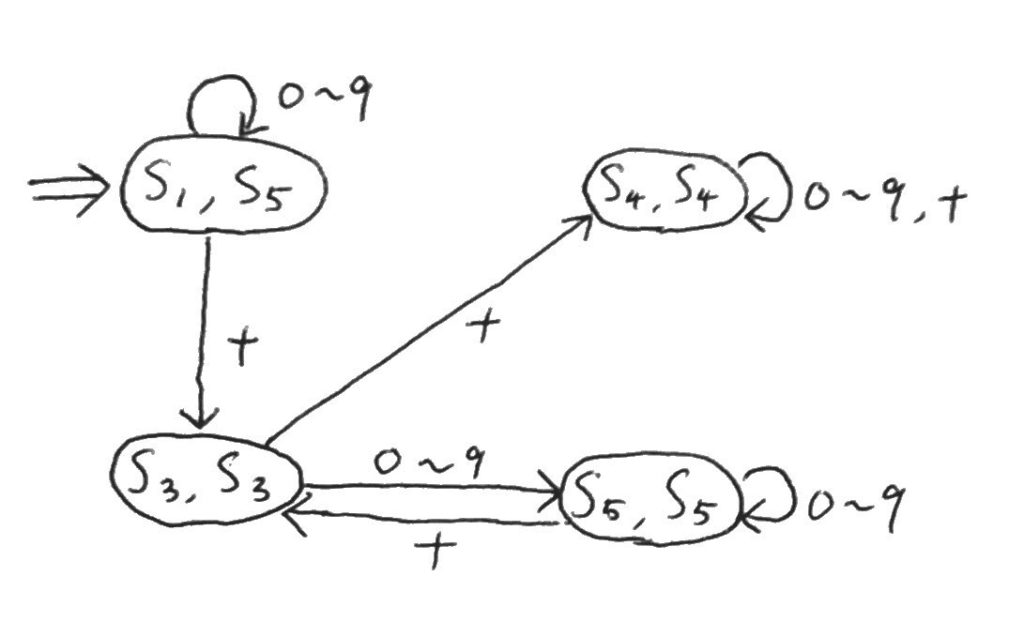
これについて、初期状態となっている$(s_1, s_5)$以外は全て同じ状態の組になっている。

つまり、明らかに受理する・しないが一致していることが分かる。

では、その$s_1, s_5$はどうかというと、これらはともに受理状態だ。

よって、各状態は全て受理状態かどうかが一致したので、$s_1, s_5$は等価だと分かった。

これを$[s_1]$としてまとめると、以下のような形になる。

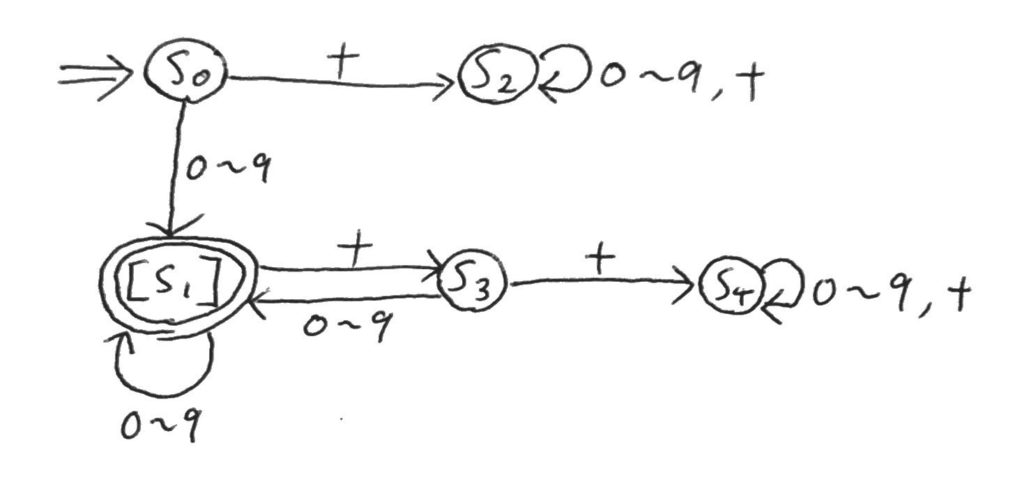
この形に対して、再度同じことをしてさらに小さくしていく。

そして、全ての2状態が等価でなくなれば、それが最小となるのだ。

なお、ここからは$s_2, s_4$と、もう一つ$s_0, s_3$もまとめられるので、今回考えている最小の有限オートマトンは以下の形になる。

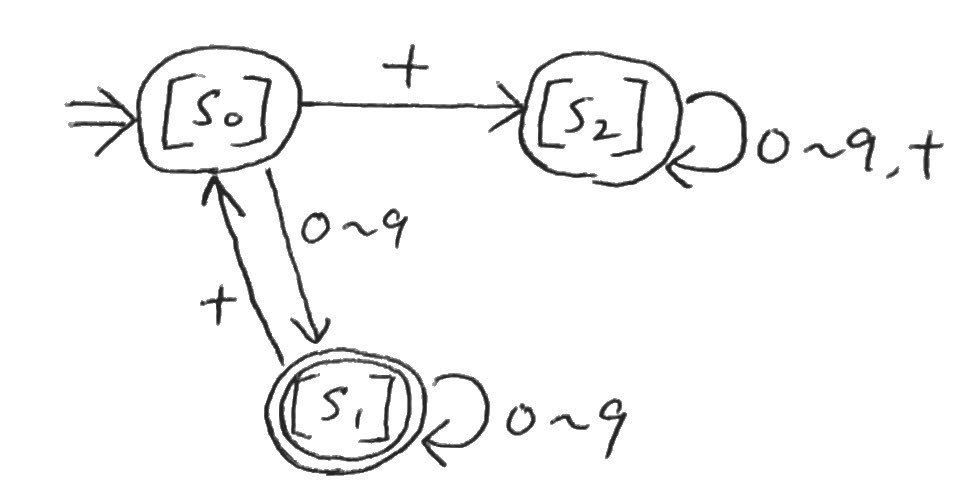
非常にスッキリした。

もし余力があれば、本当にこれで加算のみの数式を受理できるか証明してみよう。

あるいは、空列$\varepsilon$もOKとした場合の内容を考えてみてもいいかもしれない。

ちなみに、空列を許容するバージョンは、$[s_0]$を受理状態にすればいいわけではないので、それだけ注意。

そうしてしまうと、例えば1 + 2 +も受理してしまうからだ。

やるなら、元の状態で$s_0$を受理状態にし、そこから今回やったように縮小していこう。

2020/12/04追記

プログラムができたので、実際にやってみよう。

まず、縮小前の有限オートマトン$M$をプログラムで表現し、その内容を表示してみる。

状態：
	s_1
	s_0
	s_3
	s_2
	s_5
	s_4
入力記号：
	{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +}
状態遷移関数：
	δ(s_1, 0) = s_1
	δ(s_1, 1) = s_1
	δ(s_1, 2) = s_1
	δ(s_1, 3) = s_1
	δ(s_1, 4) = s_1
	δ(s_1, 5) = s_1
	δ(s_1, 6) = s_1
	δ(s_1, 7) = s_1
	δ(s_1, 8) = s_1
	δ(s_1, 9) = s_1
	δ(s_1, +) = s_3
	δ(s_0, 0) = s_1
	δ(s_0, 1) = s_1
	δ(s_0, 2) = s_1
	δ(s_0, 3) = s_1
	δ(s_0, 4) = s_1
	δ(s_0, 5) = s_1
	δ(s_0, 6) = s_1
	δ(s_0, 7) = s_1
	δ(s_0, 8) = s_1
	δ(s_0, 9) = s_1
	δ(s_0, +) = s_2
	δ(s_3, 0) = s_5
	δ(s_3, 1) = s_5
	δ(s_3, 2) = s_5
	δ(s_3, 3) = s_5
	δ(s_3, 4) = s_5
	δ(s_3, 5) = s_5
	δ(s_3, 6) = s_5
	δ(s_3, 7) = s_5
	δ(s_3, 8) = s_5
	δ(s_3, 9) = s_5
	δ(s_3, +) = s_4
	δ(s_2, 0) = s_2
	δ(s_2, 1) = s_2
	δ(s_2, 2) = s_2
	δ(s_2, 3) = s_2
	δ(s_2, 4) = s_2
	δ(s_2, 5) = s_2
	δ(s_2, 6) = s_2
	δ(s_2, 7) = s_2
	δ(s_2, 8) = s_2
	δ(s_2, 9) = s_2
	δ(s_2, +) = s_2
	δ(s_5, 0) = s_5
	δ(s_5, 1) = s_5
	δ(s_5, 2) = s_5
	δ(s_5, 3) = s_5
	δ(s_5, 4) = s_5
	δ(s_5, 5) = s_5
	δ(s_5, 6) = s_5
	δ(s_5, 7) = s_5
	δ(s_5, 8) = s_5
	δ(s_5, 9) = s_5
	δ(s_5, +) = s_3
	δ(s_4, 0) = s_4
	δ(s_4, 1) = s_4
	δ(s_4, 2) = s_4
	δ(s_4, 3) = s_4
	δ(s_4, 4) = s_4
	δ(s_4, 5) = s_4
	δ(s_4, 6) = s_4
	δ(s_4, 7) = s_4
	δ(s_4, 8) = s_4
	δ(s_4, 9) = s_4
	δ(s_4, +) = s_4
初期状態：s_0
受理状態：
	s_1
	s_5

上の状態遷移図と見比べてみれば、表現できることが分かると思う。

では、これを最小形に変換し、その結果を表示してみる。

状態：
	[s_0, s_3]
	[s_1, s_5]
	[s_2, s_4]
入力記号：
	{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +}
状態遷移関数：
	δ([s_0, s_3], 0) = [s_1, s_5]
	δ([s_0, s_3], 1) = [s_1, s_5]
	δ([s_0, s_3], 2) = [s_1, s_5]
	δ([s_0, s_3], 3) = [s_1, s_5]
	δ([s_0, s_3], 4) = [s_1, s_5]
	δ([s_0, s_3], 5) = [s_1, s_5]
	δ([s_0, s_3], 6) = [s_1, s_5]
	δ([s_0, s_3], 7) = [s_1, s_5]
	δ([s_0, s_3], 8) = [s_1, s_5]
	δ([s_0, s_3], 9) = [s_1, s_5]
	δ([s_0, s_3], +) = [s_2, s_4]
	δ([s_1, s_5], 0) = [s_1, s_5]
	δ([s_1, s_5], 1) = [s_1, s_5]
	δ([s_1, s_5], 2) = [s_1, s_5]
	δ([s_1, s_5], 3) = [s_1, s_5]
	δ([s_1, s_5], 4) = [s_1, s_5]
	δ([s_1, s_5], 5) = [s_1, s_5]
	δ([s_1, s_5], 6) = [s_1, s_5]
	δ([s_1, s_5], 7) = [s_1, s_5]
	δ([s_1, s_5], 8) = [s_1, s_5]
	δ([s_1, s_5], 9) = [s_1, s_5]
	δ([s_1, s_5], +) = [s_0, s_3]
	δ([s_2, s_4], 0) = [s_2, s_4]
	δ([s_2, s_4], 1) = [s_2, s_4]
	δ([s_2, s_4], 2) = [s_2, s_4]
	δ([s_2, s_4], 3) = [s_2, s_4]
	δ([s_2, s_4], 4) = [s_2, s_4]
	δ([s_2, s_4], 5) = [s_2, s_4]
	δ([s_2, s_4], 6) = [s_2, s_4]
	δ([s_2, s_4], 7) = [s_2, s_4]
	δ([s_2, s_4], 8) = [s_2, s_4]
	δ([s_2, s_4], 9) = [s_2, s_4]
	δ([s_2, s_4], +) = [s_2, s_4]
初期状態：[s_0, s_3]
受理状態：
	[s_1, s_5]

というわけで、上に出した状態遷移図の通りになった。

おわりに

気がついたら記事がだいぶ長くなってしまった。

しかし、今回解説した内容もはやり重要なので、少なくとも直積オートマトンや等価、各定理が何を言っているかは理解しておこう。

さて、次回は本の内容であれば非決定性有限オートマトンというものに進んでいく…のだが。

最後の具体例で書いた等価な状態について、判定と縮小を行うプログラムを先に作ってしまおう。

今のところ、言語はJavaで作るつもりでいる。

今回の内容が分かっていること前提で話を進めていくので、復習しながら進めていこう。

2020/12/04追記

ようやくプログラムができた…

あれこれ考えていたら非常に長くなってしまった。

以下の記事で解説しているので、興味があれば覗いてみてほしい。

2020/12/05追記

プログラムは別枠なので、その次の記事へのリンクはこちらに貼っておこう。

非決定性有限オートマトン…ではなく、有限オートマトンの等価と、言語の補集合を認識する有限オートマトンについて解説している。

有限オートマトンの等価に関しては、今回の状態の等価と非常に似ている。

判定用のアルゴリズムも載せているので、よかったら見てみてほしい。

オマケ：さりげなく使っていた内容の証明

…今回の証明の中で、実は証明せずに使っていた内容がある。

有限オートマトン$M = (K, \Sigma, \delta, s_0, F)$について、$s \in K$とする。

このとき、任意の列$x_1, x_2 \in \Sigma^*$に対し、以下が成立する。

$$\hat{\delta}(s, x_1x_2) = \hat{\delta}(\hat{\delta}(s, x_1), x_2)$$

意味的に考えれば、本文中に書いた通り、まず$x_1$で遷移し、その後$x_2$で遷移することと$x_1x_2$という列で遷移することなので成り立つように思える。

本文中では片方記号だったりしたが、これが言えれば$x_1$や$x_2$を長さ1の列とすることで使うことができるようになる。

一応、今回参考にした文献の中では証明なしで使われていた。

しかし、個人的には証明した方が良さそうに思えた。

そんなに難しくもないので、証明してしまおう。

$|x_1x_2|$に関する帰納法で証明する。

まず、$|x_1x_2| = 0$のとき、これは両方とも空列しかあり得ない。

そのため、左辺は$\hat{\delta}(s, \varepsilon \varepsilon) = \hat{\delta}(s, \varepsilon) = s$となる。

右辺は$\hat{\delta}(\hat{\delta}(s, \varepsilon), \varepsilon) = \hat{\delta}(s, \varepsilon) = s$。

よって、両方とも同じになったので成立だ。

次に、$x_2 = x’_2a$($a \in \Sigma$)とし、$x_1x’_2$については成り立っていると仮定する。

$$\hat{\delta}(s, x_1x’_2) = \hat{\delta}(\hat{\delta}(s, x_1), x’_2)$$

これで、$x_1x’_2a$について見ていこう。

つまり、以下が成り立つことを示す。

$$\hat{\delta}(s, x_1x’_2a) = \hat{\delta}(\hat{\delta}(s, x_1), x’_2a)$$

左辺から順番に式変形をしていく。

まず、$\hat{\delta}(s, x_1x’_2a) = \delta(\hat{\delta}(s, x_1x’_2), a)$、$\hat{\delta}$の定義から変形した。

次に、$\delta(\hat{\delta}(s, x_1x’_2), a) = \delta(\hat{\delta}(\hat{\delta}(s, x_1), x’_2), a)$、帰納法の仮定からだ。

そして、$\delta(\hat{\delta}(\hat{\delta}(s, x_1), x’_2), a) = \hat{\delta}(\hat{\delta}(s, x_1), x’_2a)$、最初と同じく$\hat{\delta}$の定義で、今度は逆方向に変形。

これで、$\hat{\delta}(s, x_1x’_2a) = \hat{\delta}(\hat{\delta}(s, x_1), x’_2a)$が言えたので、成立だ。

現状態\(s\)	入力\(a\)	次状態\(\delta(s, a)\)
\(s_0\)	0～9	\(s_1\)
\(s_0\)	+	\(s_2\)
\(s_1\)	0～9	\(s_1\)
\(s_1\)	+	\(s_3\)
\(s_2\)	0～9	\(s_2\)
\(s_2\)	+	\(s_2\)
\(s_3\)	0～9	\(s_5\)
\(s_3\)	+	\(s_4\)
\(s_4\)	0～9	\(s_4\)
\(s_4\)	+	\(s_4\)
\(s_5\)	0～9	\(s_5\)
\(s_5\)	+	\(s_3\)

日	月	火	水	木	金	土
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

オートマトン・言語と計算理論「直積オートマトンと状態の等価性」

直積オートマトン

参考書の具体例

有限オートマトン\(M_1\)

有限オートマトン\(M_2\)

直積オートマトン

到達不可能な状態

状態の等価性

等価な状態を考える理由

等価を使った定理

定理1：等価な状態とより少ない状態数の有限オートマトン

補題1：等価な状態からの遷移

補題2：変形前後の受理状態

補題3：列に対する遷移

メインの証明

定理2：定理1の逆

定理3：等価な2状態を見つける方法

実際に状態を減らしてみた

おわりに

オマケ：さりげなく使っていた内容の証明

コメント