本シリーズでは、以下の本に沿って解説を書いている。

前回まで、有限オートマトンに関するあれこれを書いてきた。
有限オートマトン自体の定義は以下の記事。
そして、直積オートマトンと、状態の等価性は以下の記事だ。
今回は、本筋からちょっと外れて、この有限オートマトンをプログラムで組んでみよう。
もちろん、等価な状態をまとめる処理も実装する。
これを使えば、面倒な計算もコンピュータに任せることができる。
エラー処理についても、例外処理の練習で実装してみよう。
なお、言語はJavaを使用している。
また、ざっと頭の中で考えながら書いているので、厳密に見ると抜け漏れ等あるかもしれない。
それと、今これを書いている段階ではテストも大してしていないので、もしこれを参考に何か作るのであれば、しっかりテストは行ってほしい。
その点、ご了承の上ご覧いただければ幸いだ。
全体方針
今回は、有限オートマトンを一つのクラスとして定義する。
その中身を考えていくのだが、まずはメンバ変数を決定する。
その後外部から呼び出せるメソッドを決めてしまい、その中でどんな処理をするかと入出力を決定しよう。
そして、そこから別途必要な処理をprivateで定義していく、という流れで進めようと思う。
メンバ変数
まず、保持したい情報は当然以下5つだろう。
- 状態の有限集合
- 入力記号の集合
- 状態遷移関数の定義
- 初期状態
- 受理状態の集合
つまり、これら5つを表現するメンバ変数を定義することになる。
さて、今回は集合やマップといったコレクション型を扱って実装しようと思うので、先に状態や入力記号の型を決めてしまった方がよさそうだ。
今回は、状態はString型、入力記号は1文字なのでchar型と決めてしまう。
これで、各メンバ変数の型と、ついでに名前も決めてしまおう。
/**
* 状態の集合
*/
private Set<String> statusSet;
/**
* 入力記号の集合
*/
private Set<Character> sigmaSet;
/**
* 状態遷移関数の定義
*/
private Map<String, Map<Character, String>> deltaMap;
/**
* 初期状態
*/
private String startStatus;
/**
* 受理状態の集合
*/
private Set<String> acceptanceStatusSet;一つ、状態遷移関数について補足をしておく。
元の定義では、状態遷移関数は二つの引数を持ち、一つの状態を表す形になっていた。
今回は、二つのマップを使い、これを表現している。
イメージとしては、まずそれぞれの状態\(s \in K\)ごとに、記号\(a \in \Sigma\)による遷移\(f_s(a) = \delta(s, a)\)が定義されている。
そして、全体のマップ\(f\)に対し、\(s\)から\(f_s\)への対応を格納している、というような感覚だ。
そのため、使う際には、まず状態\(s\)で対応\(f_s\)を取り出し、その\(f_s\)で記号\(a\)から次状態を得る、という流れになる。
外部からの呼び出し
先に、このクラスに対してどんなことができると嬉しいかを書き出してみよう。
- 各入力から、有限オートマトンを構成する(コンストラクタ)
- ある状態\(s \in K\)について、記号\(a \in \Sigma\)による遷移先\(\delta(s, a)\)を求める
- ある状態\(s \in K\)について、列\(x \in \Sigma^*\)による遷移先\(\delta(s, x)\)を求める
- 入力列\(x \in \Sigma^*\)が受理されるかどうかを判定する
- 直積オートマトンを生成する
- 同じ言語を認識する最小の有限オートマトンへ変形する
- 有限オートマトンの各情報を表示する
このくらいだろうか。
というわけで、これらの処理に対応するメソッド、あるいはコンストラクタをpublicで定義することになる。
それぞれ、入出力や処理方針を見ていこう。
コンストラクタ
コンストラクタでは、メンバ変数に対応する5つの情報を受け取り、それをメンバ変数に持つインスタンスを生成していこう。
ただ、それが本当に有限オートマトンの情報として適切かも判定したい。
それと、例えば到達できない状態や、使わない状態遷移の定義など、あっても処理上困らないが無駄なものもここで省いてしまった方がよさそうだ。
ということで、ここでの処理の流れとしては以下の通り。
- 引数を、対応するメンバ変数へ代入する
- 有限オートマトンの定義として問題ないかを確認する
- 無駄な情報を省く
処理1は、わざわざ別関数に切り出す必要もないだろう。
ただし、処理2と3はちょっと多くなりそうなので、別メソッドで処理を行うようにしよう。
また、ここでもう一つ考えたいのが、例外だ。
処理2で何かしら問題があると分かった場合、引数が不正だという内容で例外を出したい。
そこで、非チェック例外のIllegalArgumentExceptionを継承した自作例外をそれぞれ作り、それをここで呼び出し元に通知するようにしよう。
自作例外は複数作るが、継承元のIllegalArgumentExceptionをthrowsに入れれば大丈夫だろう。
では、その処理2、処理3の中身を見ていく。
処理2:定義確認
ここでの入力は、特に必要ない。
先に代入されているメンバ変数の情報を使えばいいからだ。
そして、出力としては、問題が無ければtrueを返すようにしよう。
問題があった時は、上に書いた通り対応する自作例外を呼び出し元に通知する。
では、どんなチェックを行うかだが、ここでは以下の3つで十分だ。
- 状態遷移関数について、
- 全ての状態\(s \in K\)、記号\(a\)による遷移\(\delta(s, a)\)が定義されているか
- 全ての状態\(s \in K\)、記号\(a\)による遷移先\(\delta(s, a)\)が、状態の集合に含まれているか
- 初期状態\(s_0\)が状態の集合に含まれているか
この3つとしているのは、定義が不足しているからだ。
実は、定義に忠実に従おうとすると、他にも見るべきであろう内容はある。
例えば、状態の集合に含まれていない状態\(s’ \not \in K\)による遷移\(\delta(s’, a)\)が定義されていないかや、受理状態の集合\(F\)が状態の集合の部分集合になっているかなど。
しかし、これについては定義されていたところで使わないだけで、処理自体にはあってもなくても影響はない。
なので、処理3の削除で併せて消してしまうことで解決する。
ということで、このチェックを行う処理の流れを以下に示す。
- 全ての状態\(s \in K\)について、以下を行う
- メンバ変数
deltaMapのキーに\(s\)が無かったら、例外を発生させる - 全ての入力記号\(a \in \Sigma\)について、以下を行う
- 状態遷移\(\delta(s, a)\)が定義されていなければ、例外を発生させる
- 状態遷移の結果\(\delta(s, a)\)が状態の集合\(K\)の要素でなければ、例外を発生させる
- メンバ変数
- 初期状態\(s_0\)が状態の集合\(K\)の要素でなければ、例外を発生させる
trueを返す
こんな感じで問題ないだろう。
例外を計4か所で発生させるが、それぞれは全て自作例外で、IllegalArgumentExceptionを継承したものを使おう。
ここで使う自作例外は以下二つ。
- IllegalDeltaException (状態遷移関数に関する例外)
- IllegalStartStatusException (初期状態に関する例外)
これらの中身は、全て文字列でエラーメッセージを一つ受け取り、継承元のコンストラクタを呼ぶコンストラクタのみ。
それは最後に一つソースを見せることとして、ここではすでに定義されているものとして使わせてもらう。
これを実際に組んでみると、以下のような形になった。
/**
* 有限オートマトンの定義に沿った内容かどうかを判定する関数。
* @return 定義に問題が無ければ、true
* @throws IllegalArgumentException 定義に問題があれば、対応する例外を発生させる。
*/
private boolean isLegitimateAutomaton() throws IllegalArgumentException{
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
if(!this.deltaMap.containsKey(status)) {
throw new IllegalDeltaException("状態" + status + "からの遷移が定義されていません。");
}
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
Map<Character, String> innerDeltaMap = this.deltaMap.get(status);
if(!innerDeltaMap.containsKey(symbol)) {
throw new IllegalDeltaException("状態" + status + "から、記号" + symbol + "による遷移が定義されていません。");
}
String nextStatus = innerDeltaMap.get(symbol);
if(!this.statusSet.contains(nextStatus)) {
throw new IllegalDeltaException("状態" + status + "から、記号" + symbol + "による遷移先" + nextStatus + "が状態の集合に含まれていません。");
}
}
}
if(!this.statusSet.contains(this.startStatus)) {
throw new IllegalStartStatusException("初期状態" + this.startStatus + "が状態の集合に含まれていません。");
}
return true;
}処理3:無駄な定義の削除
次にここだ。
まず引数と戻り値なのだが…ここではメンバ変数の情報を使い、操作もメンバ変数に対して行うだけなので、両方とも必要ない。
そして、例外もここでは発生するものはない。
では、処理を考えよう。
まず、やりたいことは3つ。
- 初期状態から到達できない状態を削除する
- 不要な状態遷移の定義を削除する
- 不要な受理状態の定義を削除する
順番に見ていこう。
まず、初期状態から到達できない状態の削除だが、ちょっと考え方を変えて、初期状態から到達できるもののみにする、としよう。
そうすれば、以下の方針で状態の集合を作り直すことができる。
- 新たな集合\(K’\)を定義し、その要素に初期状態\(s_0\)を入れておく
- 以下を繰り返す
- 現時点での\(K’\)の要素数を
old_sizeに入れておく - 全ての状態\(s \in K’\)について、以下を行う
- 全ての入力記号\(a \in \Sigma\)について、以下を行う
- \(\delta(s, a)\)を集合\(K”\)に入れておく
- 全ての入力記号\(a \in \Sigma\)について、以下を行う
- \(K’\)に\(K”\)の要素を追加する
- この時点での\(K’\)の要素数を
new_sizeに入れておく old_size < new_sizeであれば2-1に戻る
- 現時点での\(K’\)の要素数を
- \(K’\)を新たな状態の集合として、メンバ変数に代入する
アルゴリズムで見ると複雑そうだが、やっていることはそのまま初期状態から順番に辿っていき、新しいものが無くなるまで繰り返し辿った状態を追加しているだけ。
これで、到達できない状態は削除することができた。
なお、処理2-2-1-1で\(\delta(s, a)\)を求めているが、これは後で定義する関数delta()を使うことにしよう。
ここでは必ず定義内の入力を使うので、異常系が発生することはない。
次に、状態遷移関数の無駄を省いていく。
…のだが、ここも必要なものだけを残す方針でやっていこう。
- 全ての状態\(s \in K\)について、以下を行う
- 全ての入力記号\(a \in \Sigma\)について、以下を行う
- マップ\(f’_s(a) = \delta(s, a)\)を定義する
- マップ\(f'(s) = f’_s\)を定義する
- 全ての入力記号\(a \in \Sigma\)について、以下を行う
- \(f’\)を新たな状態遷移の定義として、メンバ変数に代入する
これも結局は使うもののみを取り出して定義し直しているだけ。
最後に、受理状態の集合から無駄なものを省いていく。
これは、そのまま省く方針で問題ないだろう。
- 全ての状態\(s \in F\)について、以下を行う
- \(s \not \in K\)であれば、集合\(F’\)に\(s\)を追加する
- \(F\)から\(F’\)の要素を削除する
これで、余分なものを全て削除できる。
ということで、組んでみた結果が以下だ。
/**
* 不必要な定義を削除する関数。
* 削除対象は、到達不可な状態、未使用の状態遷移の定義、未使用の受理状態。
*/
private void removeUnusedDefinition() {
Set<String> newStatusSet = new HashSet<>();
newStatusSet.add(this.startStatus);
int old_size, new_size;
do {
old_size = newStatusSet.size();
Set<String> addingStatusSet = new HashSet<>();
for(Iterator<String> newStatusIterator = newStatusSet.iterator(); newStatusIterator.hasNext(); ) {
String status = newStatusIterator.next();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
addingStatusSet.add(nextStatus);
}
}
newStatusSet.addAll(addingStatusSet);
new_size = newStatusSet.size();
}while(old_size < new_size);
this.statusSet = newStatusSet;
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
newInnerDeltaMap.put(symbol, nextStatus);
}
newDeltaMap.put(status, newInnerDeltaMap);
}
this.deltaMap = newDeltaMap;
Set<String> removingAcceptanceSet = new HashSet<>();
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
String status = acceptanceStatusIterator.next();
if(!this.statusSet.contains(status)) {
removingAcceptanceSet.add(status);
}
}
this.acceptanceStatusSet.removeAll(removingAcceptanceSet);
}コンストラクタの処理
中身の処理が実装できたので、ここでまとめよう。
コンストラクタでやることを以下に再掲する。
- 引数を、対応するメンバ変数へ代入する
- 有限オートマトンの定義として問題ないかを確認する
- 無駄な情報を省く
後は組んでいくだけ…なのだが。
入力はいずれもnullになっているとまずいだろう。
そこで、代入する前にnullかどうかをチェックし、nullであれば引数の異常なのでIllegalArgumentExceptionを発生させるようにしよう。
単純にif文を幾つか書けばいい。
ということで、これを実装すると以下のようになる。
/**
* 有限オートマトンのインスタンスを生成するコンストラクタ。
* @param statusSet 状態の集合
* @param sigmaSet 入力記号の集合
* @param deltaMap 状態遷移関数の定義
* @param startStatus 初期状態
* @param acceptanceStatusSet 受理状態の集合
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public FiniteAutomaton(
Set<String> statusSet,
Set<Character> sigmaSet,
Map<String, Map<Character, String>> deltaMap,
String startStatus,
Set<String> acceptanceStatusSet
) throws IllegalArgumentException {
if(statusSet == null) {
throw new IllegalArgumentException("状態の集合がnullです。");
}
if(sigmaSet == null) {
throw new IllegalArgumentException("入力記号の集合がnullです。");
}
if(deltaMap == null) {
throw new IllegalArgumentException("状態遷移関数の定義がnullです。");
}
if(startStatus == null) {
throw new IllegalArgumentException("初期状態がnullです。");
}
if(acceptanceStatusSet == null) {
throw new IllegalArgumentException("受理状態の集合がnullです。");
}
this.statusSet = statusSet;
this.sigmaSet = sigmaSet;
this.deltaMap = deltaMap;
this.startStatus = startStatus;
this.acceptanceStatusSet = acceptanceStatusSet;
if(isLegitimateAutomaton()) {
removeUnusedDefinition();
}
}記号による状態遷移
先に上の中で使ってしまったが、改めて定義していこう。
引数は遷移元の状態、遷移させる記号の二つで、戻り値は遷移後の状態だ。
そして、ここでは例外を考える必要がある。
パターンとしては、以下二つが挙げられる。
- 入力された状態が、このインスタンスの状態の集合の要素でない場合
- 入力された記号が、このインスタンスの入力記号の集合の要素でない場合
これを先にチェックして、不正であったらやはり引数がまずいのでIllegalArgumentExceptionを継承した自作例外を発生させる。
例外は以下二つを新たに定義しよう。
- NotExistsStatusException (存在しない状態に関する例外)
- NotExistsInputSymbolException (存在しない入力記号に関する例外)
中身はさっきの二つと同じだ。
入力となる状態を\(s\)、記号を\(a\)とすると、処理の中身は以下のようになる。
- \(s \not \in K\)であれば例外を発生させる
- \(a \not \in \Sigma\)であれば例外を発生させる
- \(\delta(s, a)\)を返す
ということで、これを実装したものが以下だ。
/**
* 現状態nowStatus、記号symbolによる次状態δ(nowStatus, symbol)を返す関数。
* @param nowStatus 現状態
* @param symbol 入力記号
* @return 次状態δ(nowStatus, symbol)
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public String delta(String nowStatus, char symbol) throws IllegalArgumentException{
if(!this.statusSet.contains(nowStatus)) {
throw new NotExistsStatusException("入力された状態" + nowStatus + "が状態の集合に含まれていません。");
}
if(!this.sigmaSet.contains(symbol)) {
throw new NotExistsInputSymbolException("入力された記号" + symbol + "が入力記号の集合に含まれていません。");
}
return this.deltaMap.get(nowStatus).get(symbol);
}列による状態遷移
一つ上で記号に対する状態遷移を行った。
今度は、列に拡張しよう。
元の定義通り、こちらもオーバーロードして同じ名前のメソッドを定義する。
引数は、状態と今度は列をString型で受け取ろう。
戻り値はもちろん状態から列による遷移を行った後の状態。
処理も、入力された状態から、列を1文字ずつ読んで遷移させていくだけ。
この遷移には、上の関数が使える。
なお、例外処理についてはここで特別何かをする必要はない。
もし何かまずければ、上の関数側で例外が発生するので、ここでは呼び出し元に通知するだけだ。
/**
* 現状態nowStatus、列lineによる次状態δ(nowStatus, line)を返す関数。
* @param nowStatus 現状態
* @param line 入力列
* @return 次状態δ(nowStatus, line)
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public String delta(String nowStatus, String line) throws IllegalArgumentException{
String status = nowStatus;
for(int i = 0; i < line.length(); i++) {
status = delta(status, line.charAt(i));
}
return status;
}列の受理判定
これは、上で列に対する状態遷移を定義したので、非常にシンプルになる。
入力は列\(x \in \Sigma^*\)で、出力は受理されればtrue、受理されなければfalseだ。
例外も、上で定義した中のものをそのまま呼び出し元に通知すれば済む。
方針は以下の通り。
- 初期状態\(s_0\)から列\(x\)による遷移先\(s\)を取得する
- \(s \in F\)なら
true、\(s \not \in F\)ならfalseを返す
これを実装したものが以下だ。
/**
* 列lineが受理されるかどうかを判定する関数。
* @param line 入力列
* @return lineが受理されればtrue、受理されなければfalse
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public boolean isAccept(String line) throws IllegalArgumentException{
String status = delta(this.startStatus, line);
return this.acceptanceStatusSet.contains(status);
}直積オートマトンの生成
ここから、ちょっと考えなければいけないことが増えてくる。
復習で、有限オートマトン\(M_1 = (K_1, \Sigma, \delta_1, s_0, F_1)\)、\(M_2 = (K_2, \Sigma, \delta_2, t_0, F_2)\)の直積オートマトン\(M = (K, \Sigma, \delta, (s_0, t_0), F)\)は以下のように定義されていた。
- \(K = \{\delta((s_0, t_0), x) | x \in \Sigma^*\} \subset K \times K\)
- \(\delta((s, t), a) = (\delta_1(s, a), \delta_2(t, a))\)
※\(s \in K_1, t \in K_2, a \in \Sigma\) - \(F \subset K\)
このとき、受理状態の集合\(F\)は条件によって変化したことを思い出そう。
ある状態\((s, t) \in K\)が受理状態に入るかどうかは、例えば…
- 元の両オートマトンで受理される必要があれば、\(s \in F_1\)かつ\(t \in F_2\)
- 元のどちらかの有限オートマトンで受理されればいいのであれば、\(s \in F_1\)または\(t \in F_2\)
となっていればよかった。
しかし、ここではどうすればいいか分からない。
そこで、この部分についてはフラグとして受け取り、それによって処理を分岐させよう。
今回は、上に出した二つを定義する。
ということで、そのフラグを定数で定義してしまおう。
/**
* 直積オートマトン生成時のフラグ、両オートマトンで受理されるものを受理する
*/
public static final int ACCEPT_AND = 0;
/**
* 直積オートマトン生成時のフラグ、少なくとも片方の有限オートマトンで受理されるものを受理する
*/
public static final int ACCEPT_OR = 1;では、メソッドに戻ってくる。
受け取る引数は計3つ、直積させる有限オートマトンのインスタンス二つと、このフラグだ。
そして、戻り値はこの直積オートマトンのインスタンスになる。
今回は引数で受け取った情報のみを使用するため、静的メソッドで定義しよう。
さて、処理の中身について考えるのだが、ここでは引数のチェックのみを考える。
なぜかというと、後で解説する最小形への変形の中でも直積オートマトンを作る必要がある。
最終的に同じことをするので、実際にインスタンスを作る部分については一つにまとめたい。
そのため、どちらでも対応できる形で実処理の部分を作成し、ここではそれを呼び出すだけにしたいのだ。
ということで、引数チェック。
直積オートマトンでチェックする必要があるのは、入力記号が一致しているかどうか。
その他、フラグが想定されたものかも見る必要がある。
前者は入力記号に関する例外なので、再度IllegalArgumentExceptionを継承して、今度はDifferentInputSymbolExceptionというものを作成する。
中身は上で作ったものと同じ。
後者は、純粋な引数エラーなので、そのままIllegalArgumentExceptionを使えばいいだろう。
一旦ここまでで、後の具体的な中身は後で定義する関数を呼び出す。
その引数や戻り値もその時解説するとして、ここでは定義されているものとして処理を書いてしまおう。
/**
* 直積オートマトンを生成する関数。
* @param M1 直積させる有限オートマトンのインスタンス
* @param M2 直積させる有限オートマトンのインスタンス
* @param acceptanceSetFlug 直積オートマトンの受理状態に関するフラグ、0もしくは1
* @return 直積オートマトンのインスタンス
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる
*/
public static FiniteAutomaton makeProductAutomaton(
FiniteAutomaton M1,
FiniteAutomaton M2,
int acceptanceSetFlug
) throws IllegalArgumentException{
if(!M1.sigmaSet.containsAll(M2.sigmaSet)) {
throw new DifferentInputSymbolException("直積させる2つの有限オートマトンの入力記号の集合が異なります。");
}
if(!M2.sigmaSet.containsAll(M1.sigmaSet)) {
throw new DifferentInputSymbolException("直積させる2つの有限オートマトンの入力記号の集合が異なります。");
}
if(acceptanceSetFlug < 0 || acceptanceSetFlug > 1) {
throw new IllegalArgumentException("受理状態に関するフラグが不正です。");
}
return FiniteAutomaton.makeProductAutomaton(
M1,
M2,
M1.startStatus,
M2.startStatus,
acceptanceSetFlug
);
}最小形への変形
ここが一番処理が長くなる部分だろう。
先に入出力を考える…のだが、必要な情報はメンバ変数に揃っており、それに対して操作を行うだけなので、引数や戻り値はなしだ。
そして、例外も発生させることはない。
ということで、処理の中身を考えていく…前に、どんな方針で最小形へ変形できたか、復習しておこう。
まず、縮小対象となる有限オートマトンを\(M = (K, \Sigma, \delta, s_0, F)\)とする。
このとき、\(K\)内の等価な2状態を見つけ、それをひとまとめにすることで縮小することができた。
状態\(s\)と等価な状態の集合を\([s] = \{s’ \in K | s \equiv s’\}\)とし、縮小後の有限オートマトン\(M’ = (K’, \Sigma, \delta’, s’_0, F’)\)は以下のようになっている。
- \(K’ = \{[s] | s \in K\}\)
- \(\delta'([s], a) = [\delta(s, a)]\) ※\(a \in \Sigma\)
- \(s’_0 = [s_0]\)
- \(F’ = \{[s] \in K | s \in F\}\)
ということで、まずは等価な状態の集合を求め、それを使って縮小すればいい。
その、等価な状態の集合をどうやって求めるかだが、ここで直積オートマトンを生成する必要がある。
ここも復習しておこう。
有限オートマトン\(M = (K, \Sigma, \delta, s_0, F)\)内の2状態\(s_1, s_2 \in K\)が等価であるかどうかを確かめたいとする。
このとき、特別な直積オートマトン\(M[s_i, s_j] = (K’, \Sigma, \delta’, (s_i, s_j), F’)\)を生成する。
また、初期状態から到達できない状態は既に省かれているとする。
このとき、\(M[s_i, s_j]\)内の状態\((s_k, s_l) \in K’\)について…
- \(s_k \in F \Leftrightarrow s_l \not \in F\)となっている状態が一つでもあれば、\(s_i \not \equiv s_j\)
- 全て\(s_k \in F \Leftrightarrow s_l \in F\)であれば、\(s_i \equiv s_j\)
となっていた。
これらを使って、縮小する方針を考えると以下のようになるだろう。
- \(K\)内の要素を、等価な状態ごとに一つの集合\([s]\)にまとめ、その集合を\(K’\)とする
- \(K’\)を使い、縮小後の有限オートマトン\(M’\)を構成し、その各要素をメンバ変数へ代入する
ということで、これら二つを処理する関数を切り出して考えよう。
先に、中身が定義されているとして、この関数を書いてしまう。
/**
* 同じ言語を認識する最小の有限オートマトンへ変形する関数。
*/
public void shrinkAutomaton() {
Set<Set<String>> equivStatusSetSet = getEquivStatusSetSet();
shrinkAllEquivStatus(equivStatusSetSet);
}等価な状態ごとの集合を求める処理
ここでは、新たに入力を受け取る必要はない。
戻り値については、ちょっと複雑だ。
まず、ある状態\(s \in K\)について、それと等価な状態を全て求めて一つの集合\([s]\)としておく。
そして、戻り値はこの集合を要素とする集合になる。
つまり、型の書き方でいうとSet<Set<String>>となるのだ。
では、ここの処理方針を。
- 戻り値用の集合\(R\)を用意しておく
- チェック済みの状態の集合\(C\)を用意しておく
- 全ての状態\(s \in K\)に対し、以下を行う
- \(s \in C\)であれば、次の要素\(s\)に進む
- 集合\([s]\)を用意し、\(s\)を追加する
- \(C\)に\(s\)を追加する
- 全ての\(s’ \in K\)について、以下を行う
- \(s’ \in C\)であれば、次の要素\(s’\)に進む
- \(s \equiv s’\)であれば、\([s]\)に\(s’\)を追加する
- \(R\)に集合\([s]\)を要素として追加する
- \(C\)に集合\([s]\)の全ての要素を追加する
- \(R\)を返す
こんな感じだろうか。
では、この処理3-4-2で行う、2状態が等価であるかどうかを判定する関数も考えよう。
こちらでは、入力はこの2状態でいいだろう。
説明の都合上、入力された2状態は\(s_i, s_j\)とさせてもらう。
そして、出力は\(s_i \equiv s_j\)ならtrue、\(s_i \not \equiv s_j\)ならfalseだ。
ここの処理方針は以下の通り。
- 直積オートマトン\(M[s_i, s_j]\)を生成する
- 全ての\(s \in K\)について、以下を行う
- 全ての\(s’ \in K\)について、以下を行う
- \((s, s’)\)が\(M[s_i, s_j]\)の状態であれば、以下を行う
- \(s \in F\)の判定結果と\(s’ \in F\)の判定結果が異なれば、
falseを返す
- \(s \in F\)の判定結果と\(s’ \in F\)の判定結果が異なれば、
- \((s, s’)\)が\(M[s_i, s_j]\)の状態であれば、以下を行う
- 全ての\(s’ \in K\)について、以下を行う
trueを返す
これで問題ない。
さて、ようやく直積オートマトンが出てきたので、この中身も考えていこう。
まず、ここでは直積させる二つの有限オートマトンは両方とも自身、かつ初期状態が特殊で、\((s_i, s_j)\)となっている。
そして、上で考えていた直積オートマトンについては、入力は二つの有限オートマトン\(M_1, M_2\)、初期状態はそれぞれの初期状態、そして追加で受理状態をどうするかのフラグも必要だった。
これらから、共通する直積オートマトン生成の処理を考えていく。
入力は二つの有限オートマトンのインスタンス\(M_1, M_2\)、それぞれにおける初期状態\(s_0, t_0\)、受理状態のフラグの計5つあれば十分だろう。
なお、等価判定時の直積オートマトンは受理状態は一切関係ないので、用意したどちらを入れても問題ない。
そのため、常にANDのフラグを入れておくこととしよう。
また、インスタンスの情報は使わないので、これも静的メソッドで定義する。
出力は、直積オートマトンのインスタンスだ。
ここは定義通りに直積オートマトンを作っていくだけなので、処理方針は省略する。
ちなみに、インスタンス生成時に到達不可な状態を省くよう処理を決めてあるので、ここで再度行う必要はない。
代わりに、一つ約束事を設けよう。
直積オートマトンにおける状態の表し方だ。
数式の定義では、\((s_i, s_j)\)といった形になっていた。
それに併せ、プログラム上でも(s_i, s_j)のような形で表すとする。
この時、後で文字列一致による状態の判別を行いたいので、余分な文字やスペースを入れないよう注意だ。
ということで、これを組むと以下のようになる。
/**
* 直積オートマトンを生成する関数。
* @param M1 直積させる有限オートマトンのインスタンス
* @param M2 直積させる有限オートマトンのインスタンス
* @param startStatus1 M1の初期状態
* @param startStatus2 M2の初期状態
* @param acceptanceSetFlug 受理状態に関するフラグ、0もしくは1
* @return M1とM2の直積オートマトン
*/
private static FiniteAutomaton makeProductAutomaton(
FiniteAutomaton M1,
FiniteAutomaton M2,
String startStatus1,
String startStatus2,
int acceptanceSetFlug
) {
Set<String> newStatusSet = new HashSet<>();
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
for(Iterator<String> status1Iterator = M1.statusSet.iterator(); status1Iterator.hasNext(); ) {
String status1 = status1Iterator.next();
for(Iterator<String> status2Iterator = M2.statusSet.iterator(); status2Iterator.hasNext(); ) {
String status2 = status2Iterator.next();
String newStatus = "(" + status1 + ", " + status2 + ")";
newStatusSet.add(newStatus);
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = M1.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus1 = M1.delta(status1, symbol);
String nextStatus2 = M2.delta(status2, symbol);
String newNextStatus = "(" + nextStatus1 + ", " + nextStatus2 + ")";
newInnerDeltaMap.put(symbol, newNextStatus);
}
newDeltaMap.put(newStatus, newInnerDeltaMap);
}
}
String newStartStatus = "(" + startStatus1 + ", " + startStatus2 + ")";
Set<String> newAcceptanceStatusSet = new HashSet<>();
if(acceptanceSetFlug == FiniteAutomaton.ACCEPT_AND) {
for(Iterator<String> acceptanceStatus1Iterator = M1.acceptanceStatusSet.iterator(); acceptanceStatus1Iterator.hasNext(); ) {
String acceptanceStatus1 = acceptanceStatus1Iterator.next();
for(Iterator<String> acceptanceStatus2Iterator = M2.acceptanceStatusSet.iterator(); acceptanceStatus2Iterator.hasNext(); ) {
String acceptanceStatus2 = acceptanceStatus2Iterator.next();
String newAcceptanceStatus = "(" + acceptanceStatus1 + ", " + acceptanceStatus2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
}else if(acceptanceSetFlug == FiniteAutomaton.ACCEPT_OR) {
for(Iterator<String> status1Iterator = M1.statusSet.iterator(); status1Iterator.hasNext(); ) {
String status1 = status1Iterator.next();
for(Iterator<String> acceptanceStatus2Iterator = M2.acceptanceStatusSet.iterator(); acceptanceStatus2Iterator.hasNext(); ) {
String acceptanceStatus2 = acceptanceStatus2Iterator.next();
String newAcceptanceStatus = "(" + status1 + ", " + acceptanceStatus2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
for(Iterator<String> acceptanceStatus1Iterator = M1.acceptanceStatusSet.iterator(); acceptanceStatus1Iterator.hasNext(); ) {
String acceptanceStatus1 = acceptanceStatus1Iterator.next();
for(Iterator<String> status2Iterator = M2.statusSet.iterator(); status2Iterator.hasNext(); ) {
String status2 = status2Iterator.next();
String newAcceptanceStatus = "(" + acceptanceStatus1 + ", " + status2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
}
return new FiniteAutomaton(
newStatusSet,
M1.sigmaSet,
newDeltaMap,
newStartStatus,
newAcceptanceStatusSet
);
}これを元に、二つの状態\(s_i, s_j\)が等価であるかどうかを判定する関数を作成する。
/**
* 2状態が等価かどうかを判定する関数。
* @param status1 等価判定を行う状態
* @param status2 等価判定を行う状態
* @return 2状態が等価であればtrue、非等価であればfalse
*/
private boolean isEquivStatus(String status1, String status2) {
FiniteAutomaton M = FiniteAutomaton.makeProductAutomaton(
this,
this,
status1,
status2,
FiniteAutomaton.ACCEPT_AND
);
String[] statusArray = new String[this.statusSet.size()];
this.statusSet.toArray(statusArray);
for(int i = 0; i < statusArray.length; i++) {
for(int j = 0; j < statusArray.length; j++) {
String status = "(" + statusArray[i] + ", " + statusArray[j] + ")";
if(M.statusSet.contains(status)) {
if(this.acceptanceStatusSet.contains(statusArray[i]) != this.acceptanceStatusSet.contains(statusArray[j])) {
return false;
}
}
}
}
return true;
}さらにこれを使って、等価な状態ごとの集合を返す関数を作ろう。
/**
* 等価な状態の集合の集合を得る関数
* @return 等価な状態の集合の集合
*/
private Set<Set<String>> getEquivStatusSetSet(){
Set<Set<String>> equivStatusSetSet = new HashSet<>();
Set<String> checkedStatusSet = new HashSet<>();
String[] statusArray = new String[this.statusSet.size()];
this.statusSet.toArray(statusArray);
for(int i = 0; i < statusArray.length; i++) {
if(checkedStatusSet.contains(statusArray[i])) {
continue;
}
Set<String> equivStatusSet = new HashSet<>();
equivStatusSet.add(statusArray[i]);
checkedStatusSet.add(statusArray[i]);
for(int j = 0; j < statusArray.length; j++) {
if(checkedStatusSet.contains(statusArray[j])) {
continue;
}
if(isEquivStatus(statusArray[i], statusArray[j])) {
equivStatusSet.add(statusArray[j]);
}
}
equivStatusSetSet.add(equivStatusSet);
checkedStatusSet.addAll(equivStatusSet);
}
return equivStatusSetSet;
}等価な状態をひとまとめにする処理
上で、等価な状態ごとの集合を得られた。
あとは、それを使って縮小するだけだ。
今、入力としてこの等価な状態ごとの集合を受け取る。
これを元にメンバ変数をいじるので、関数としての戻り値はなしだ。
ここも、定義通りに各定義をしていき、メンバ変数に入れるだけなので方針は大丈夫だろう。
代わりに、ここでも一つ書き方を決めておく。
縮小した後の状態の書き方だ。
数式の定義では、\(s\)と等価な状態を\([s]\)として縮小していた。
しかし、これではどの状態を縮小したのかが分からない。
そこで、\([s] = \{s_1, s_2, …, s_n\}\)として、プログラムでは[s_1, s_2, ..., s_n]と表現することにしよう。
また、縮小しない場合には、大括弧はつけないとする。
これで、どれを縮約したかが分かるようになる。
以上から問題なく組める…と思っていたのだが、一つ厄介なことがある。
今回使っている、HashSetに関してだ。
公式ドキュメントによると、中身の順序は保証されていない。
そのため、中身を列挙する形で表記を定義したのに、再度取り出すと今度は別の順序になっている可能性もあるということだ。
このままでは色々と不都合が生じるので、苦肉の策だが、一つの等価な状態の集合ごとに繰り返し縮小を行うことにしよう。
これだと無駄なメモリを使ったり処理をしたりすることになるが、分かりやすさも欲しいので許してほしい。
というわけで、まずはある一つの等価な状態をまとめる処理を実装する。
/**
* ある等価な状態の集合を縮小する関数。
* @param equivStatusSet 縮小を行う等価な状態の集合
*/
private void shrinkEquivStatus(Set<String> equivStatusSet) {
Set<String> newStatusSet = new HashSet<>();
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
String newStartStatus = "";
Set<String> newAcceptanceStatusSet = new HashSet<>();
for(Iterator<String> it = this.statusSet.iterator(); it.hasNext(); ) {
String status = it.next();
if(!equivStatusSet.contains(status)) {
newStatusSet.add(status);
}
}
String equivStatusString = "[";
for(Iterator<String> equivStatusIterator = equivStatusSet.iterator(); equivStatusIterator.hasNext(); ) {
equivStatusString += equivStatusIterator.next();
if(equivStatusIterator.hasNext()) {
equivStatusString += ", ";
}
}
equivStatusString += "]";
newStatusSet.add(equivStatusString);
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
if(equivStatusSet.contains(nextStatus)) {
newInnerDeltaMap.put(symbol, equivStatusString);
}else {
newInnerDeltaMap.put(symbol, nextStatus);
}
}
if(equivStatusSet.contains(status)) {
newDeltaMap.put(equivStatusString, newInnerDeltaMap);
}else {
newDeltaMap.put(status, newInnerDeltaMap);
}
}
if(equivStatusSet.contains(this.startStatus)) {
newStartStatus = equivStatusString;
}else {
newStartStatus = this.startStatus;
}
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
String acceptanceStatus = acceptanceStatusIterator.next();
if(equivStatusSet.contains(acceptanceStatus)) {
newAcceptanceStatusSet.add(equivStatusString);
}else {
newAcceptanceStatusSet.add(acceptanceStatus);
}
}
this.statusSet = newStatusSet;
this.deltaMap = newDeltaMap;
this.startStatus = newStartStatus;
this.acceptanceStatusSet = newAcceptanceStatusSet;
}あとは、これを要素が二つ以上の全ての等価な状態の集合に対して行ってあげればいい。
/**
* 全ての等価な状態の集合を縮小する関数。
* @param equivStatusSetSet 等価な状態の集合の集合
*/
private void shrinkAllEquivStatus(Set<Set<String>> equivStatusSetSet) {
for(Iterator<Set<String>> equivStatusSetIterator = equivStatusSetSet.iterator(); equivStatusSetIterator.hasNext(); ) {
Set<String> equivStatusSet = equivStatusSetIterator.next();
if(equivStatusSet.size() > 1) {
shrinkEquivStatus(equivStatusSet);
}
}
}情報表示
ここは、このインスタンスが持つ情報をコンソールに表示するのみ。
引数、戻り値はともになし、例外も考えない。
各要素をひたすらコンソール出力していくだけなので、処理方針もいらないだろう。
/**
* 有限オートマトンの各情報をコンソールに表示する関数。
*/
public void showAutomatonInformation() {
System.out.println("状態:");
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
System.out.println("\t" + statusIterator.next());
}
System.out.println("入力記号:");
System.out.print("\t{");
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
System.out.print(sigmaIterator.next());
if(sigmaIterator.hasNext()) {
System.out.print(", ");
}
}
System.out.println("}");
System.out.println("状態遷移関数:");
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String nowStatus = statusIterator.next();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char a = sigmaIterator.next();
System.out.println("\tδ(" + nowStatus + ", " + a + ") = " + delta(nowStatus, a));
}
}
System.out.println("初期状態:" + this.startStatus);
System.out.println("受理状態:");
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
System.out.println("\t" + acceptanceStatusIterator.next());
}
}ちなみに、表示例は以下のようになる。
状態:
s_1
s_0
s_3
s_2
入力記号:
{0, 1}
状態遷移関数:
δ(s_1, 0) = s_0
δ(s_1, 1) = s_3
δ(s_0, 0) = s_1
δ(s_0, 1) = s_2
δ(s_3, 0) = s_2
δ(s_3, 1) = s_1
δ(s_2, 0) = s_3
δ(s_2, 1) = s_0
初期状態:s_0
受理状態:
s_0これは、本編で例に使った「0と1からなる列で、0と1の個数がともに偶数個である列」を受理する有限オートマトンだ。
この状態遷移図を以下に載せておこう。
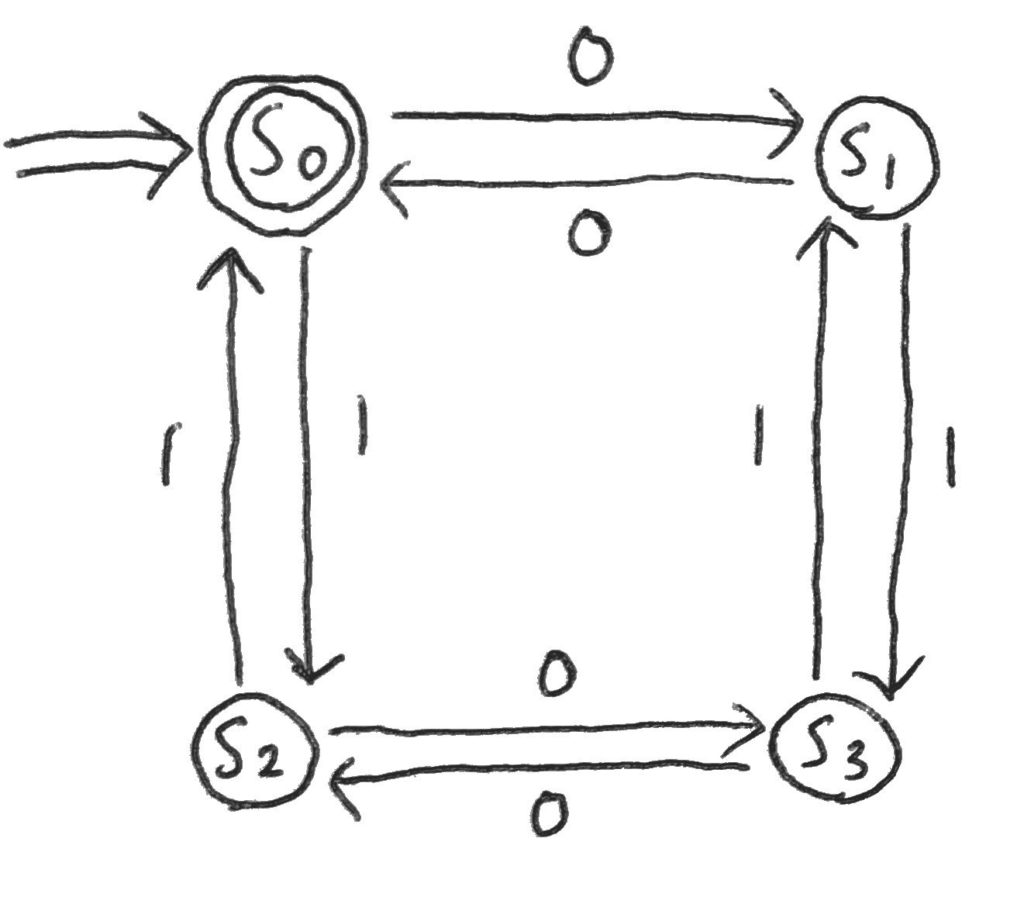
ソースコード全体
ようやく、全てを組むことができた。
今回組んだソースコード全体像を見ていこう。
まず、各クラスのパッケージに関しては以下のような構造になっている。
- modelパッケージ
- FiniteAutomatonクラス
- exceptionパッケージ
- DifferentInputSymbolExceptionクラス
- IllegalDeltaExceptionクラス
- IllegalStartStatusExceptionクラス
- NotExistsInputSymbolExceptionクラス
- NotExistsStatusExceptionクラス
各自作例外クラスは、中で定義しているものは全て文字列を引数とするコンストラクタのみ、やっていることも継承元のIllegalArgumentExceptionのコンストラクタを呼んでいるだけ。
そのため、うち一つだけ例として出しておこう。
package model.exception;
/**
* 直積オートマトン生成時の入力記号に関する例外。
* @author シノ
*
*/
public class DifferentInputSymbolException extends IllegalArgumentException {
public DifferentInputSymbolException(String msg) {
super(msg);
}
}
では、本題の有限オートマトンを表現するクラスを載せよう。
非常に長いが、ここまでの内容を全て入れているだけだ。
package model;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
import model.exception.DifferentInputSymbolException;
import model.exception.IllegalDeltaException;
import model.exception.IllegalStartStatusException;
import model.exception.NotExistsInputSymbolException;
import model.exception.NotExistsStatusException;
/**
* 有限オートマトンを表現するクラス。
* @author シノ
*
*/
public class FiniteAutomaton {
/**
* 直積オートマトン生成時のフラグ、両オートマトンで受理されるものを受理する
*/
public static final int ACCEPT_AND = 0;
/**
* 直積オートマトン生成時のフラグ、少なくとも片方の有限オートマトンで受理されるものを受理する
*/
public static final int ACCEPT_OR = 1;
/**
* 状態の集合
*/
private Set<String> statusSet;
/**
* 入力記号の集合
*/
private Set<Character> sigmaSet;
/**
* 状態遷移関数の定義
*/
private Map<String, Map<Character, String>> deltaMap;
/**
* 初期状態
*/
private String startStatus;
/**
* 受理状態の集合
*/
private Set<String> acceptanceStatusSet;
/**
* 有限オートマトンのインスタンスを生成するコンストラクタ。
* @param statusSet 状態の集合
* @param sigmaSet 入力記号の集合
* @param deltaMap 状態遷移関数の定義
* @param startStatus 初期状態
* @param acceptanceStatusSet 受理状態の集合
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public FiniteAutomaton(
Set<String> statusSet,
Set<Character> sigmaSet,
Map<String, Map<Character, String>> deltaMap,
String startStatus,
Set<String> acceptanceStatusSet
) throws IllegalArgumentException {
if(statusSet == null) {
throw new IllegalArgumentException("状態の集合がnullです。");
}
if(sigmaSet == null) {
throw new IllegalArgumentException("入力記号の集合がnullです。");
}
if(deltaMap == null) {
throw new IllegalArgumentException("状態遷移関数の定義がnullです。");
}
if(startStatus == null) {
throw new IllegalArgumentException("初期状態がnullです。");
}
if(acceptanceStatusSet == null) {
throw new IllegalArgumentException("受理状態の集合がnullです。");
}
this.statusSet = statusSet;
this.sigmaSet = sigmaSet;
this.deltaMap = deltaMap;
this.startStatus = startStatus;
this.acceptanceStatusSet = acceptanceStatusSet;
if(isLegitimateAutomaton()) {
removeUnusedDefinition();
}
}
/**
* 現状態nowStatus、記号symbolによる次状態δ(nowStatus, symbol)を返す関数。
* @param nowStatus 現状態
* @param symbol 入力記号
* @return 次状態δ(nowStatus, symbol)
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public String delta(String nowStatus, char symbol) throws IllegalArgumentException{
if(!this.statusSet.contains(nowStatus)) {
throw new NotExistsStatusException("入力された状態" + nowStatus + "が状態の集合に含まれていません。");
}
if(!this.sigmaSet.contains(symbol)) {
throw new NotExistsInputSymbolException("入力された記号" + symbol + "が入力記号の集合に含まれていません。");
}
return this.deltaMap.get(nowStatus).get(symbol);
}
/**
* 現状態nowStatus、列lineによる次状態δ(nowStatus, line)を返す関数。
* @param nowStatus 現状態
* @param line 入力列
* @return 次状態δ(nowStatus, line)
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public String delta(String nowStatus, String line) throws IllegalArgumentException{
String status = nowStatus;
for(int i = 0; i < line.length(); i++) {
status = delta(status, line.charAt(i));
}
return status;
}
/**
* 列lineが受理されるかどうかを判定する関数。
* @param line 入力列
* @return lineが受理されればtrue、受理されなければfalse
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる。
*/
public boolean isAccept(String line) throws IllegalArgumentException{
String status = delta(this.startStatus, line);
return this.acceptanceStatusSet.contains(status);
}
/**
* 直積オートマトンを生成する関数。
* @param M1 直積させる有限オートマトンのインスタンス
* @param M2 直積させる有限オートマトンのインスタンス
* @param acceptanceSetFlug 直積オートマトンの受理状態に関するフラグ、0もしくは1
* @return 直積オートマトンのインスタンス
* @throws IllegalArgumentException 入力に問題があれば、対応する例外を発生させる
*/
public static FiniteAutomaton makeProductAutomaton(
FiniteAutomaton M1,
FiniteAutomaton M2,
int acceptanceSetFlug
) throws IllegalArgumentException{
if(!M1.sigmaSet.containsAll(M2.sigmaSet)) {
throw new DifferentInputSymbolException("直積させる2つの有限オートマトンの入力記号の集合が異なります。");
}
if(!M2.sigmaSet.containsAll(M1.sigmaSet)) {
throw new DifferentInputSymbolException("直積させる2つの有限オートマトンの入力記号の集合が異なります。");
}
if(acceptanceSetFlug < 0 || acceptanceSetFlug > 1) {
throw new IllegalArgumentException("受理状態に関するフラグが不正です。");
}
return FiniteAutomaton.makeProductAutomaton(
M1,
M2,
M1.startStatus,
M2.startStatus,
acceptanceSetFlug
);
}
/**
* 同じ言語を認識する最小の有限オートマトンへ変形する関数。
*/
public void shrinkAutomaton() {
Set<Set<String>> equivStatusSetSet = getEquivStatusSetSet();
shrinkAllEquivStatus(equivStatusSetSet);
}
/**
* 有限オートマトンの各情報をコンソールに表示する関数。
*/
public void showAutomatonInformation() {
System.out.println("状態:");
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
System.out.println("\t" + statusIterator.next());
}
System.out.println("入力記号:");
System.out.print("\t{");
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
System.out.print(sigmaIterator.next());
if(sigmaIterator.hasNext()) {
System.out.print(", ");
}
}
System.out.println("}");
System.out.println("状態遷移関数:");
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String nowStatus = statusIterator.next();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char a = sigmaIterator.next();
System.out.println("\tδ(" + nowStatus + ", " + a + ") = " + delta(nowStatus, a));
}
}
System.out.println("初期状態:" + this.startStatus);
System.out.println("受理状態:");
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
System.out.println("\t" + acceptanceStatusIterator.next());
}
}
/**
* 有限オートマトンの定義に沿った内容かどうかを判定する関数。
* @return 定義に問題が無ければ、true
* @throws IllegalArgumentException 定義に問題があれば、対応する例外を発生させる。
*/
private boolean isLegitimateAutomaton() throws IllegalArgumentException{
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
if(!this.deltaMap.containsKey(status)) {
throw new IllegalDeltaException("状態" + status + "からの遷移が定義されていません。");
}
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
Map<Character, String> innerDeltaMap = this.deltaMap.get(status);
if(!innerDeltaMap.containsKey(symbol)) {
throw new IllegalDeltaException("状態" + status + "から、記号" + symbol + "による遷移が定義されていません。");
}
String nextStatus = innerDeltaMap.get(symbol);
if(!this.statusSet.contains(nextStatus)) {
throw new IllegalDeltaException("状態" + status + "から、記号" + symbol + "による遷移先" + nextStatus + "が状態の集合に含まれていません。");
}
}
}
if(!this.statusSet.contains(this.startStatus)) {
throw new IllegalStartStatusException("初期状態" + this.startStatus + "が状態の集合に含まれていません。");
}
return true;
}
/**
* 不必要な定義を削除する関数。
* 削除対象は、到達不可な状態、未使用の状態遷移の定義、未使用の受理状態。
*/
private void removeUnusedDefinition() {
Set<String> newStatusSet = new HashSet<>();
newStatusSet.add(this.startStatus);
int old_size, new_size;
do {
old_size = newStatusSet.size();
Set<String> addingStatusSet = new HashSet<>();
for(Iterator<String> newStatusIterator = newStatusSet.iterator(); newStatusIterator.hasNext(); ) {
String status = newStatusIterator.next();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
addingStatusSet.add(nextStatus);
}
}
newStatusSet.addAll(addingStatusSet);
new_size = newStatusSet.size();
}while(old_size < new_size);
this.statusSet = newStatusSet;
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
newInnerDeltaMap.put(symbol, nextStatus);
}
newDeltaMap.put(status, newInnerDeltaMap);
}
this.deltaMap = newDeltaMap;
Set<String> removingAcceptanceSet = new HashSet<>();
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
String status = acceptanceStatusIterator.next();
if(!this.statusSet.contains(status)) {
removingAcceptanceSet.add(status);
}
}
this.acceptanceStatusSet.removeAll(removingAcceptanceSet);
}
/**
* 直積オートマトンを生成する関数。
* @param M1 直積させる有限オートマトンのインスタンス
* @param M2 直積させる有限オートマトンのインスタンス
* @param startStatus1 M1の初期状態
* @param startStatus2 M2の初期状態
* @param acceptanceSetFlug 受理状態に関するフラグ、0もしくは1
* @return M1とM2の直積オートマトン
*/
private static FiniteAutomaton makeProductAutomaton(
FiniteAutomaton M1,
FiniteAutomaton M2,
String startStatus1,
String startStatus2,
int acceptanceSetFlug
) {
Set<String> newStatusSet = new HashSet<>();
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
for(Iterator<String> status1Iterator = M1.statusSet.iterator(); status1Iterator.hasNext(); ) {
String status1 = status1Iterator.next();
for(Iterator<String> status2Iterator = M2.statusSet.iterator(); status2Iterator.hasNext(); ) {
String status2 = status2Iterator.next();
String newStatus = "(" + status1 + ", " + status2 + ")";
newStatusSet.add(newStatus);
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = M1.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus1 = M1.delta(status1, symbol);
String nextStatus2 = M2.delta(status2, symbol);
String newNextStatus = "(" + nextStatus1 + ", " + nextStatus2 + ")";
newInnerDeltaMap.put(symbol, newNextStatus);
}
newDeltaMap.put(newStatus, newInnerDeltaMap);
}
}
String newStartStatus = "(" + startStatus1 + ", " + startStatus2 + ")";
Set<String> newAcceptanceStatusSet = new HashSet<>();
if(acceptanceSetFlug == FiniteAutomaton.ACCEPT_AND) {
for(Iterator<String> acceptanceStatus1Iterator = M1.acceptanceStatusSet.iterator(); acceptanceStatus1Iterator.hasNext(); ) {
String acceptanceStatus1 = acceptanceStatus1Iterator.next();
for(Iterator<String> acceptanceStatus2Iterator = M2.acceptanceStatusSet.iterator(); acceptanceStatus2Iterator.hasNext(); ) {
String acceptanceStatus2 = acceptanceStatus2Iterator.next();
String newAcceptanceStatus = "(" + acceptanceStatus1 + ", " + acceptanceStatus2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
}else if(acceptanceSetFlug == FiniteAutomaton.ACCEPT_OR) {
for(Iterator<String> status1Iterator = M1.statusSet.iterator(); status1Iterator.hasNext(); ) {
String status1 = status1Iterator.next();
for(Iterator<String> acceptanceStatus2Iterator = M2.acceptanceStatusSet.iterator(); acceptanceStatus2Iterator.hasNext(); ) {
String acceptanceStatus2 = acceptanceStatus2Iterator.next();
String newAcceptanceStatus = "(" + status1 + ", " + acceptanceStatus2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
for(Iterator<String> acceptanceStatus1Iterator = M1.acceptanceStatusSet.iterator(); acceptanceStatus1Iterator.hasNext(); ) {
String acceptanceStatus1 = acceptanceStatus1Iterator.next();
for(Iterator<String> status2Iterator = M2.statusSet.iterator(); status2Iterator.hasNext(); ) {
String status2 = status2Iterator.next();
String newAcceptanceStatus = "(" + acceptanceStatus1 + ", " + status2 + ")";
newAcceptanceStatusSet.add(newAcceptanceStatus);
}
}
}
return new FiniteAutomaton(
newStatusSet,
M1.sigmaSet,
newDeltaMap,
newStartStatus,
newAcceptanceStatusSet
);
}
/**
* 2状態が等価かどうかを判定する関数。
* @param status1 等価判定を行う状態
* @param status2 等価判定を行う状態
* @return 2状態が等価であればtrue、非等価であればfalse
*/
private boolean isEquivStatus(String status1, String status2) {
FiniteAutomaton M = FiniteAutomaton.makeProductAutomaton(
this,
this,
status1,
status2,
FiniteAutomaton.ACCEPT_AND
);
String[] statusArray = new String[this.statusSet.size()];
this.statusSet.toArray(statusArray);
for(int i = 0; i < statusArray.length; i++) {
for(int j = 0; j < statusArray.length; j++) {
String status = "(" + statusArray[i] + ", " + statusArray[j] + ")";
if(M.statusSet.contains(status)) {
if(this.acceptanceStatusSet.contains(statusArray[i]) != this.acceptanceStatusSet.contains(statusArray[j])) {
return false;
}
}
}
}
return true;
}
/**
* 等価な状態の集合の集合を得る関数
* @return 等価な状態の集合の集合
*/
private Set<Set<String>> getEquivStatusSetSet(){
Set<Set<String>> equivStatusSetSet = new HashSet<>();
Set<String> checkedStatusSet = new HashSet<>();
String[] statusArray = new String[this.statusSet.size()];
this.statusSet.toArray(statusArray);
for(int i = 0; i < statusArray.length; i++) {
if(checkedStatusSet.contains(statusArray[i])) {
continue;
}
Set<String> equivStatusSet = new HashSet<>();
equivStatusSet.add(statusArray[i]);
checkedStatusSet.add(statusArray[i]);
for(int j = 0; j < statusArray.length; j++) {
if(checkedStatusSet.contains(statusArray[j])) {
continue;
}
if(isEquivStatus(statusArray[i], statusArray[j])) {
equivStatusSet.add(statusArray[j]);
}
}
equivStatusSetSet.add(equivStatusSet);
checkedStatusSet.addAll(equivStatusSet);
}
return equivStatusSetSet;
}
/**
* ある等価な状態の集合を縮小する関数。
* @param equivStatusSet 縮小を行う等価な状態の集合
*/
private void shrinkEquivStatus(Set<String> equivStatusSet) {
Set<String> newStatusSet = new HashSet<>();
Map<String, Map<Character, String>> newDeltaMap = new HashMap<>();
String newStartStatus = "";
Set<String> newAcceptanceStatusSet = new HashSet<>();
for(Iterator<String> it = this.statusSet.iterator(); it.hasNext(); ) {
String status = it.next();
if(!equivStatusSet.contains(status)) {
newStatusSet.add(status);
}
}
String equivStatusString = "[";
for(Iterator<String> equivStatusIterator = equivStatusSet.iterator(); equivStatusIterator.hasNext(); ) {
equivStatusString += equivStatusIterator.next();
if(equivStatusIterator.hasNext()) {
equivStatusString += ", ";
}
}
equivStatusString += "]";
newStatusSet.add(equivStatusString);
for(Iterator<String> statusIterator = this.statusSet.iterator(); statusIterator.hasNext(); ) {
String status = statusIterator.next();
Map<Character, String> newInnerDeltaMap = new HashMap<>();
for(Iterator<Character> sigmaIterator = this.sigmaSet.iterator(); sigmaIterator.hasNext(); ) {
char symbol = sigmaIterator.next();
String nextStatus = delta(status, symbol);
if(equivStatusSet.contains(nextStatus)) {
newInnerDeltaMap.put(symbol, equivStatusString);
}else {
newInnerDeltaMap.put(symbol, nextStatus);
}
}
if(equivStatusSet.contains(status)) {
newDeltaMap.put(equivStatusString, newInnerDeltaMap);
}else {
newDeltaMap.put(status, newInnerDeltaMap);
}
}
if(equivStatusSet.contains(this.startStatus)) {
newStartStatus = equivStatusString;
}else {
newStartStatus = this.startStatus;
}
for(Iterator<String> acceptanceStatusIterator = this.acceptanceStatusSet.iterator(); acceptanceStatusIterator.hasNext(); ) {
String acceptanceStatus = acceptanceStatusIterator.next();
if(equivStatusSet.contains(acceptanceStatus)) {
newAcceptanceStatusSet.add(equivStatusString);
}else {
newAcceptanceStatusSet.add(acceptanceStatus);
}
}
this.statusSet = newStatusSet;
this.deltaMap = newDeltaMap;
this.startStatus = newStartStatus;
this.acceptanceStatusSet = newAcceptanceStatusSet;
}
/**
* 全ての等価な状態の集合を縮小する関数。
* @param equivStatusSetSet 等価な状態の集合の集合
*/
private void shrinkAllEquivStatus(Set<Set<String>> equivStatusSetSet) {
for(Iterator<Set<String>> equivStatusSetIterator = equivStatusSetSet.iterator(); equivStatusSetIterator.hasNext(); ) {
Set<String> equivStatusSet = equivStatusSetIterator.next();
if(equivStatusSet.size() > 1) {
shrinkEquivStatus(equivStatusSet);
}
}
}
}
おわりに
非常に長くなってしまった。
しかし、これでプログラム上で有限オートマトンを扱うことができるようになった。
…テストは、裏でやっておこう。
終わったら、その結果をここに追記する。
一応、軽く動作確認はしてあるので、基本的には問題ない…と思いたい。
さて、これで完成にしてもいいのだが、現時点で二つほど拡張を考えている。
一つは、有限オートマトンの生成に関して。
今、あらかじめプログラム上で対応する情報をつくり、それを受け取ってインスタンスを生成している。
しかし、このままでは色々な有限オートマトンを作るのがちょいと面倒だ。
そこで、コンソールで対話形式で有限オートマトンを作ったり、あるいは決まったフォーマットで書かれたファイルを読んだりすることでインスタンスを生成できるようにしたい。
特にフォーマットができれば、逆にそれをファイルに書き出して保存しておくことも可能だ。
これは是非実装しておきたい。
もう一つは、状態遷移図の表示をしてみたい、というもの。
これはできるか分からないが、もしできればブログを書くときに使えるので非常に嬉しい。
また、実際に列を読む際に、状態遷移の様子を表現できたらよりわかりやすくなるだろう。
何か使えるものがないか、今後調べてみるとしよう。



コメント