本シリーズでは、以下の本に沿って解説を書いている。

前回は、正規言語は文脈自由言語であることを示した。
今回以降の内容にどれだけ関わるかは微妙なところではあるが、重要な定理なのでこの事実だけでも押さえておきたい。
以下がその記事だ。
さて、今回はcfgの標準形というものを扱う。
具体的には、チョムスキー標準形というものだ。
本当はグライバッハ標準形もやろうとしたのだが、かなりの長さになってしまったので二つに分けようと思う。
変換方法もご紹介するので、幾つか具体的な例で確認しておきたい。
変数、終端記号の書き方
今回の内容に入る前に、一つ注意点がある。
今後、変数や終端記号、生成規則を色々と書いていくのだが、ちょっと書き方のルールを決めようと思う。
特に断りがない場合、変数を表す際にはローマ字の大文字を使い、終端記号を表す際にはローマ字の小文字を使う。
例えば、生成規則で…
$$A \rightarrow bCdE$$
と書いたとき、\(A, C, E\)は変数、\(b, d\)は終端記号と見なすという意味だ。
特に断りなくいきなり知らない文字が出てきたら、そういう意味だと捉えて欲しい。
ちなみに、ギリシャ文字\(\alpha, \beta, \gamma\)なども使う時がある。
このとき、大体は変数の列、あるいは変数と終端記号が混じった列として扱う。
これについては、使う時に毎回明示するのでこれも気を付けておいて欲しい。
標準形
では、本題に入ろう。
まず、そもそもこの標準形とは何ぞやというところに触れようと思う。
これまで扱っていたcfg\(G = (V, \Sigma, P, S)\)の生成規則\(P\)について、ある変数\(A \in V\)と、変数と終端記号の混じった列\(\alpha \in (V \cup \Sigma)^*\)を使って以下のように書き表されていた。
$$A \rightarrow \alpha$$
言い換えると、矢印の左側は変数一つ、右側は長さ0以上の変数・終端記号の列というルールしかなかった。
このままでもいいのだが、もうちょっといい形に書き換えたい場合がある。
そこで、生成規則の右側について、特定のルールを加えるような考え方があり、そのルールに沿った形を標準形と呼んでいる。
この目的は様々で、例えば見た目を見やすくしたり、あるいはどの生成規則を使えばいいかを分かりやすくしたり、などなど。
生成する言語はそのままに形を変える、という意味ではdfaの最小化と似ている…かもしれない。
そんなことを頭の片隅に入れてもらいつつ、具体的な標準形を見ていこう。
チョムスキー標準形
あるcfg\(G = (V, \Sigma, P, S)\)に注目する。
この生成規則\(P\)の中身が以下3パターンのいずれかのみであるとき、この\(G\)をチョムスキー標準形という。
- \(S \rightarrow \varepsilon\)
- \(A \rightarrow a\) ※\(A \in V, a \in \Sigma\)
- \(A \rightarrow B_1B_2\) ※\(A, B_1, B_2 \in V\)
言葉で説明すると、まず右側が空列\(\varepsilon\)となるのは、開始記号からのみになる。
その他は、矢印の右側が終端記号一つ、あるいは変数二つとなっている形のことだ。
参考書では説明の簡略化のためなのか、矢印の右側が空列であるような生成規則を含まない場合で考えているが、本記事ではそれも含めて考えることにしよう。
では、具体例を見てみる。
以下で定義するcfg\(G = (V, \Sigma, P, S)\)はチョムスキー標準形だ。
- \(V = \{S, A, B, C, X\}\)
- \(\Sigma = \{0, 1, 2\}\)
- \(P\)について
- \(S \rightarrow AX\)
- \(S \rightarrow CC\)
- \(X \rightarrow SB\)
- \(A \rightarrow 0\)
- \(B \rightarrow 1\)
- \(C \rightarrow 2\)
どの生成規則の右側を見ても、終端記号一つか変数二つになっていることを確認してほしい。
ちなみに、この\(G\)が生成する言語\(L(G)\)は以下の通り。
$$L(G) = \{0^n221^n | n \in \mathbb{Z}, n \geq 0\}$$
任意のcfgをチョムスキー標準形に変形
どんな文脈自由言語も、このチョムスキー標準形のcfgで表せるのだろうか。
結論から言うと、表せる。
というわけで、その変換方法をご紹介しよう。
なお、方法の中で生成する言語に差がないことも確認していく。
作業内訳は、大きく以下5つだ。
- 生成先が空列の生成規則を削除する
- 余分な生成規則を削除する
- 単一規則を削除する
- 変数、終端記号が混じった列を変数のみに変換する
- 長さ3以上の変数の列を分解する
これも、参考書では3からの三つになっているが、前に二つ追加させてもらった。
では、変換元のcfgを\(G = (V, \Sigma, P, S)\)として詳細を見ていこう。
生成先が空列の生成規則を削除する
まずこれについて。
チョムスキー標準形の定義から、開始記号以外の変数から空列\(\varepsilon\)を生成するような生成規則を削除しなければいけない。
そのために、以下の操作を行う。
最初に、任意の変数\(A \in V\)について、以下の生成規則が存在するかを確認する。
$$A \rightarrow \varepsilon$$
次に、この生成規則が存在する全ての変数\(A \in V\)について、これを生成先に含むような生成規則全てに注目する。
このとき、変数\(B \in V\)と二つの列\(\alpha, \gamma \in (V \setminus \{A\} \cup \Sigma)^*\)を使って以下の形になっている。
$$B \rightarrow \alpha A \gamma$$
これについて、以下の生成規則を加える。
$$B \rightarrow \alpha \gamma$$
今は一つだけの場合で見たが、二つ以上ある場合はそれぞれについて消す、消さないの組合せ全てを入れる必要があるので注意しよう。
例えば、二つ入っている時は\(\beta \in (V \setminus \{A\}, \Sigma)^*\)を追加して…
$$B \rightarrow \alpha A \beta A \gamma$$
という形になっている。
これに対しては…
- \(B \rightarrow \alpha \beta A \gamma\)
- \(B \rightarrow \alpha A \beta \gamma\)
- \(B \rightarrow \alpha \beta \gamma\)
の三つを追加する必要がある、ということ。
そして、元の生成規則\(A \rightarrow \varepsilon\)を削除する。
以上を、生成先が空列のものが開始記号からの生成規則のみになるまで、あるいは全て無くなるまで繰り返す。
これで完了だ。
この操作が問題ない理由は明らかだろう。
空列を導出するようなステップについて、その1回をスキップするような生成規則を加えていることになるからだ。
この時点で、生成規則の右側が空列となるのは、あったとしても開始記号からの生成規則\(S \rightarrow \varepsilon\)のみになっている。
具体例は後でまとめてやるので、まずは手順の解説を進めていこう。
余分な生成規則を削除する
余分な生成規則とは、具体的な列を導出する際の任意のステップ内で使用されないような生成規則のことだ。
これを取り除いていくのが手順2となる。
…実は、これをしなくてもチョムスキー標準形自体には影響はない。
しかし、使わない生成規則があるのは無駄なので、後の作業を簡単にするためにも削除してしまおう。
この生成規則は、2パターンある。
一つ目は、それを使うと終端記号のみの列を導出できないパターン。
厳密には、変数に着目した考え方である。
どういうことかというと、以下の例を見て欲しい。
- \(S \rightarrow AB\)
- \(A \rightarrow a\)
- \(B \rightarrow b\)
- \(B \rightarrow CD\)
- \(C \rightarrow D\)
- \(D \rightarrow C\)
これを注意深く見てもらうと、四つ目の生成規則\(B \rightarrow CD\)を使った瞬間に、それ以降終端記号が出てこなくなるのが分かるだろうか。
\(C\)と\(D\)は互いを置き換えるような生成規則しかないので、具体的な終端記号は出てこなくなるのだ。
このような状況になっている生成規則は、削除しても生成する言語に影響が無くなる。
ということで、これを削除する方法は以下の通り。
まず、確認用に集合\(W\)を用意し、最初は空集合としておこう。
次に、以下を新たな変数が追加されなくなるまで繰り返す。
- 列\(\alpha \in (\Sigma \cup W)^*\)を使って\(X \rightarrow \alpha\)という生成規則が存在する変数\(X\)を\(W\)に追加する
これをすると、\(W\)は具体的な終端記号を導出できるような変数のみが含まれることになる。
最後に、この\(W\)に含まれないような変数を含む生成規則と、その変数自身を削除すれば完了だ。
上の例でやってみよう。
- \(W = \phi\)
- \(A \rightarrow a\)、\(B \rightarrow b\)より、\(W = \{A, B\}\)
- \(S \rightarrow AB\)より、\(W = \{S, A, B\}\)
これで、全て追加し終えた。
ここには変数\(C, D\)が出てこないので、これを含む生成規則として以下3つを削除できる。
- \(B \rightarrow CD\)
- \(C \rightarrow D\)
- \(D \rightarrow C\)
もちろん、生成規則で使われなくなったので、変数\(C, D\)自体も削除。
これで一つ目のパターンが完了だ。
二つ目、開始記号から始めて、どんなステップを辿っても出現しないような変数を矢印の左側に持つようなものがあるパターン。
どういうことか、こちらもちょっと具体例を出してみよう。
- \(S \rightarrow A\)
- \(A \rightarrow BC\)
- \(B \rightarrow A\)
- \(C \rightarrow BC\)
- \(D \rightarrow ABC\)
これ以外は右側に終端記号しかないとしておく。
このとき、変数\(D\)について、\(\alpha, \gamma \in (V \setminus \{D\} \cup \Sigma)^*\)を使って\(S \overset{*}{\Rightarrow} \alpha D \gamma\)というステップは存在しない。
要するに、その\(D\)から始まる生成規則は一切使われることはない。
これも、単に削除すればOKだ。
これを見つける際にも上と似た方法が使えるのだが、図を書いてみるとより分かりやすい。
まず、開始記号を〇で囲む。
次に、その開始記号からの生成規則で右側に出てくる変数それぞれを〇で囲んで配置し、矢印で結ぶ。
そして、そのそれぞれの変数でも同じことをしてあげる。
すでに配置されている変数には、新しく配置するのではなく元々書いてあるところに矢印を結べばいい。
これを繰り返していくと、最終的に開始記号から辿れる変数のみが出てくるので、その図に含まれない変数から始まる生成規則を削除する、ということになる。
上の例をこの図にすると、以下のような感じだ。
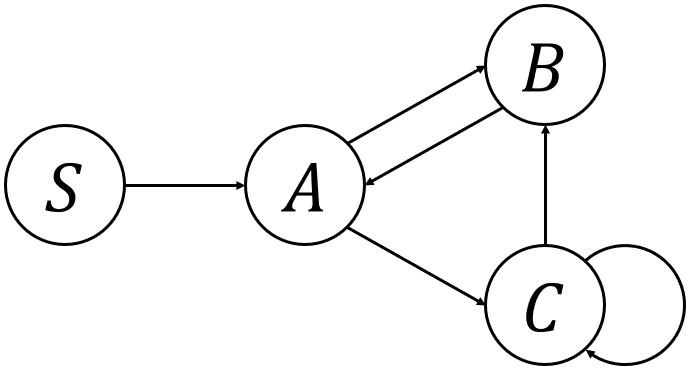
これで、\(D\)が使われていないことが容易に分かるだろう。
あるいは、例えば\(E \rightarrow e\)といった生成規則があったとしても、それも使われないことも分かる。
なお、これらはどのタイミングでやってもいいので、変換時に生成規則が多すぎるという場合はこれらで削減しながら進めていこう。
ちなみにだが、単に生成規則の右側に存在しない変数を探せばいいように思えるかもしれないが、それだと到達不可な生成規則が残ってしまう可能性がある。
例えば、以下の形。
- \(S \rightarrow A\)
- \(A \rightarrow BC\)
- \(B \rightarrow A\)
- \(C \rightarrow BC\)
- \(D \rightarrow ABC\)
- \(D \rightarrow E\)
- \(E \rightarrow S\)
- \(E \rightarrow D\)
この右側には、全ての変数が出てきている。
しかし、図を書くと先ほどのものと全く同じ、つまり変数\(D, E\)が出てこないのだ。
あくまで、開始記号から辿れるかがポイント。
一応生成できる列に差はないのだが、気を付けておいて欲しい。
単一規則を削除する
ここからは参考書にも載っている内容になる。
手順の説明の前に、単一規則について説明しておこう。
生成規則のうち、二つの変数\(A, B \in V\)を使って以下の形で書き表せる生成規則を単一規則と呼ぶことにする。
$$A \rightarrow B$$
要するに、単に変数を置き換えるだけのような生成規則のことだ。
これはチョムスキー標準形の定義に含まれない形なので、なんとかして無くしたい、というわけだ。
その手順は以下の通り。
まず、任意の異なる2変数\(A, B \in V\)について、以下のようなステップが存在するかを確認する。
$$A \overset{*}{\Rightarrow} B$$
このステップはどうやっても単一規則のみでしか導出できないので、実際に見る時は単一規則のみを見ればいい。
ここで、ある変数\(A\)から、\(B_1, B_2, …, B_n \in V \setminus \{A\}\)に対して上のようなステップが存在したとしよう。
このとき、\(B_1, B_2, …, B_n\)から始まる単一規則でないような生成規則があるかを探す。
あれば、その生成規則の始点を\(A\)に置き換えたものを追加する。
例えば、ある\(B_i\)について、\(\alpha \in (V \cup \Sigma)^*\)を使って、単一規則でないような以下の生成規則があったとする。
$$B_i \rightarrow \alpha$$
このときは、以下の生成規則を追加すればいい。
$$A \rightarrow \alpha$$
これを全ての変数について行い、最後に単一規則を全て削除すればOKだ。
ここでは、単一規則を含むようなステップについて、その単一規則の部分をすっ飛ばすような生成規則を追加しているので、生成できる列に差がないことは容易に分かるだろう。
ちなみに、単一規則によるステップ先の変数からの単一規則以外の生成規則が存在しない場合は、特に追加する必要はない。
これも、結局は変数をより具体的な列にすることはできない状態なので、後で削除してしまっても支障はない。
変数、終端記号が混じった列を変数のみに変換する
4つ目の作業に入ろう。
今、作業3までで、生成規則の右側は以下いずれかになっている。
- 空列\(\varepsilon\) ※開始記号からのみ
- 終端記号ただ一つ
- 変数のみの長さが2以上の列
- その他(終端記号のみ、あるいは変数を含む長さ2以上の列)
今回の作業で取り除くのは、四つ目の部分だ。
まず、この四つ目に該当する生成規則を全て持ってくる。
次に、その生成規則の右側に含まれる終端記号それぞれについて、それただ一つを生成するような生成規則を追加する。
例えば、\(A \rightarrow bCdE\)という生成規則があったときは…
- \(X_B \rightarrow b\)
- \(X_D \rightarrow d\)
の二つを追加すればいい。
もちろんだが、追加する時の変数は新しく作ろう。
そして、今作った生成規則の変数で、終端記号を置き換えたものを追加し、元の生成規則を削除する。
上の例では、以下の生成規則を作り出すことになる。
$$A \rightarrow X_BCX_DE$$
そして、\(A \rightarrow bCdE\)は削除、となる。
これを条件に当てはまる全ての生成規則に対してやってあげよう。
これは、直接変数を生成していたところに今度はステップを追加しているだけなので、生成する列に変化はない。
ちなみに、例えば元々その記号のみを生成するような生成規則があった時、それを使えばいいのでは?と思われるかもしれない。
これは、状況によっては使えるが、使えない場合もある。
例えば、上の例…\(A \rightarrow bCdE\)で\(b\)と\(d\)について、別で以下二つの生成規則が元々存在したとする。
- \(B \rightarrow b\)
- \(D \rightarrow d\)
これについて、まず変数\(B\)からの生成規則がこれのみであった場合には、新しく変数を追加せずこれを使うことができる。
しかし、変数\(D\)について、別の生成規則が一つでもあった場合には、これを使うことはできない。
例えば\(D \rightarrow AC\)という生成規則があったとしよう。
すると、本来は終端記号一つのみなのに、\(A \overset{*}{\Rightarrow} bCACE\)のようなステップが新たに導出できるようになってしまうからだ。
…私も最初勘違いしていたので、気を付けて欲しい。
長さ3以上の変数の列を分解する
さて、ここまでの内容で、生成規則の右側は以下の3パターンいずれかになっている。
- 空列\(\varepsilon\) ※開始記号からのみ
- 終端記号ただ一つ
- 変数のみの長さが2以上の列
あとは、三つ目のうち長さが3以上の変数列を、長さが2になるよう調整してあげればいい。
この生成規則について、3以上の整数\(n\)を使って以下のようになっていたとしよう。
$$A \rightarrow B_1B_2…B_n$$
このとき、以下の生成規則と、その時に現れた変数\(C_1, C_2, …, C_{n – 2}\)を追加する。
- \(A \rightarrow B_1C_1\)
- \(C_1 \rightarrow B_2C_2\)
- \(C_2 \rightarrow B_3C_3\)
- …
- \(C_{n – 3} \rightarrow B_{n – 2}C_{n – 2}\)
- \(C_{n – 2} \rightarrow B_{n – 1}B_n\)
そして、元の生成規則\(A \rightarrow B_1B_2…B_n\)を削除すれば完了だ。
これも、結局はステップを追加しているだけなので、生成できる列に変化がないことは自明だろう。
これを全ての対象について行うと、生成規則はチョムスキー標準形の定義に沿った形になっている。
必要に応じて不要な生成規則を手順2で改めて削除し、完成だ。
具体例その1
では、二つほど具体的なcfgをチョムスキー標準形に変形してみよう。
まず、参考書の例。
変換元のcfg\(G = (V, \Sigma, P, A)\)を以下のように定義する。
- \(V = \{A, B, C, D, E, F\}\)
- \(\Sigma = \{a, b\}\)
- \(P\)について
- \(A \rightarrow B\)
- \(A \rightarrow C\)
- \(B \rightarrow D\)
- \(D \rightarrow E\)
- \(E \rightarrow B\)
- \(C \rightarrow F\)
- \(B \rightarrow b\)
- \(E \rightarrow ADa\)
- \(C \rightarrow ABB\)
これをチョムスキー標準形に直してみよう。
まず、手順1…については、今空列\(\varepsilon\)のみを生成する生成規則がないので飛ばしてOK。
ということで、手順2から始めよう。
余分な生成規則を削除していく。
まず終端記号を作り出せない変数について。
手順通り、集合\(W\)を用意してやってみよう。
- \(W = \phi\)
- \(B \rightarrow b\)より、\(W = \{B\}\)
- \(A \rightarrow B\)、\(E \rightarrow B\)より、\(W = \{A, B, E\}\)
- \(D \rightarrow E\)、\(C \rightarrow ABB\)より、\(W = \{A, B, C, D, E\}\)
これ以上は\(W\)に追加できない。
つまり、出てきていない変数\(F\)と、それを含む生成規則が削除可能だ。
具体的に書くと、\(C \rightarrow F\)の一つだけが削除できる。
この時点で生成規則は以下のようになる。
- \(A \rightarrow B\)
- \(A \rightarrow C\)
- \(B \rightarrow D\)
- \(D \rightarrow E\)
- \(E \rightarrow B\)
- \(B \rightarrow b\)
- \(E \rightarrow ADa\)
- \(C \rightarrow ABB\)
次に、開始記号から辿れない生成規則について。
先ほど紹介した図を書いてみよう。
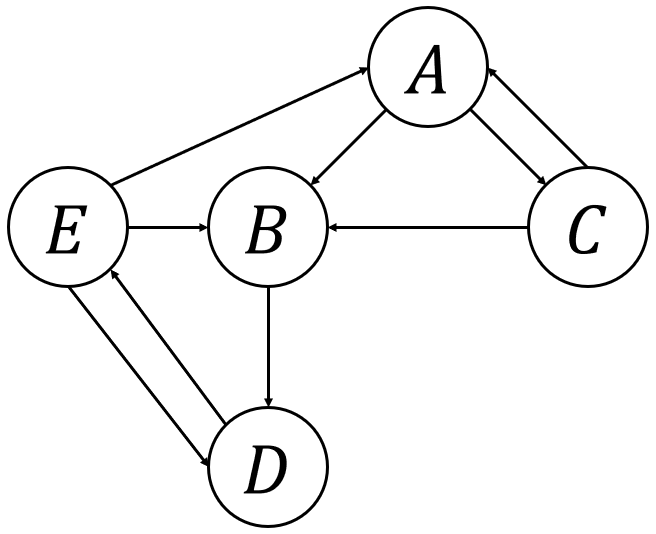
このように、全ての変数に辿ることができるので、これ以上は削除することができない。
ということで手順の2が完了だ。
ではここから本題、手順3に進む。
まずは各変数から、単一規則のみで辿れるようなステップを見ていく。
ちなみにだが、ここも図を書いてみると分かりやすい。
先ほどの図と似ているが、今度は全ての単一規則のみを使って表してみる。
すると、以下の通り。
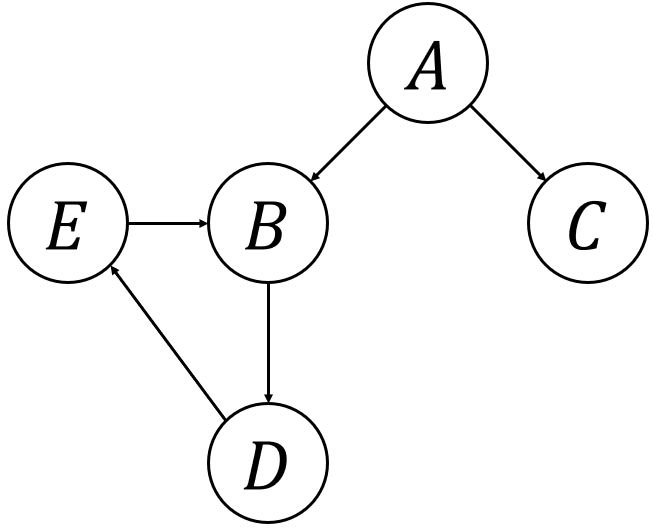
あとは、それぞれの変数から矢印で辿れる範囲が、今回探したい単一規則のみで辿れるステップになっている。
各変数について、どの変数へ辿れるか求めてみよう。
- \(A\) : \(B, C, D, E\)
- \(B\) : \(D, E\)
- \(C\) : なし
- \(D\) : \(B, E\)
- \(E\) : \(B, D\)
こうなった。
あとは、それぞれの単一規則でないような生成規則に着目していく。
\(A\)について、他の全ての変数に辿れるので…
- \(A \rightarrow b\)
- \(A \rightarrow ADa\)
- \(A \rightarrow ABB\)
この3つを追加だ。
以降、\(B\)、\(D\)、\(E\)もやっていくと…
- \(B \rightarrow ADa\)
- \(D \rightarrow b\)
- \(D \rightarrow ADa\)
- \(E \rightarrow b\)
この4つが求まる。
以上から、この計7個を足し、単一規則を取り除いた以下10個が生成規則となる。
- \(A \rightarrow b\)
- \(A \rightarrow ADa\)
- \(A \rightarrow ABB\)
- \(B \rightarrow ADa\)
- \(D \rightarrow b\)
- \(D \rightarrow ADa\)
- \(E \rightarrow b\)
- \(B \rightarrow b\)
- \(E \rightarrow ADa\)
- \(C \rightarrow ABB\)
これで作業3が完了だ。
…ちなみにだが、この時点で変数\(C, E\)が右側に登場しなくなる。
つまり、この二つから始まる生成規則も到達不可となるので、取り除いてしまおう。
それ以外は全て開始記号\(A\)から辿れるのでこれ以上は取り除けない。
結果、以下の7個だ。
- \(A \rightarrow b\)
- \(A \rightarrow ADa\)
- \(A \rightarrow ABB\)
- \(B \rightarrow ADa\)
- \(D \rightarrow b\)
- \(D \rightarrow ADa\)
- \(B \rightarrow b\)
では、次の手順4に進んでいこう。
ここでは、長さが2以上、かつ終端記号が入った生成先について、変数のみに変形していく。
今、右側がこの条件に合致するものは1種類、\(ADa\)という列だ。
よって、新しく\(X \rightarrow a\)を追加し、\(ADa\)を\(ADX\)に置き換えよう。
これで、以下8個になる。
- \(A \rightarrow b\)
- \(A \rightarrow ADX\)
- \(A \rightarrow ABB\)
- \(B \rightarrow ADX\)
- \(D \rightarrow b\)
- \(D \rightarrow ADX\)
- \(B \rightarrow b\)
- \(X \rightarrow a\)
この\(X\)は、終端記号\(a\)を生成するような生成規則しかないので、一つを使いまわせていることに気を付けよう。
心配なら、全て別の変数で生成規則を作ってもいい。
では最後の手順5だ。
長さ3以上の変数列を分解していく。
今回は以下2パターンが存在する。
- \(ADX\)
- \(ABB\)
つまり、二つの生成規則を追加すればいい。
- \(Y_1 \rightarrow DX\)
- \(Y_2 \rightarrow BB\)
これを使って、それぞれ置き換えて…
- \(A \rightarrow b\)
- \(A \rightarrow AY_1\)
- \(A \rightarrow AY_2\)
- \(B \rightarrow AY_1\)
- \(D \rightarrow b\)
- \(D \rightarrow AY_1\)
- \(B \rightarrow b\)
- \(X \rightarrow a\)
- \(Y_1 \rightarrow DX\)
- \(Y_2 \rightarrow BB\)
こんな感じ。
この\(Y_1\)、\(Y_2\)も一つの生成規則しかないので使いまわせている。
今回のように対象となる生成規則の生成先が全く同じ列であればその中では使いまわせるので、覚えておくといいかもしれない。
あるいは、心配であればこちらも全て別の生成規則を追加しておこう。
これで、チョムスキー標準形の完成だ。
具体例その2
一つ目の例は、空列を生成するような生成規則がないものだった。
今度は、それがあるようなものでやってみよう。
Wikipediaの例を拝借し、今回対象とするcfg\(G = (V, \Sigma, P, S)\)を以下のように定義する。
- \(V = \{S, B\}\)
- \(\Sigma = \{a, b, c\}\)
- \(P\)について
- \(S \rightarrow aSc\)
- \(S \rightarrow B\)
- \(B \rightarrow bBc\)
- \(B \rightarrow \varepsilon\)
ちなみに、上のリンクにも書かれているが、この\(G\)が生成する言語\(L(G)\)は以下だ。
$$L(G) = \{a^nb^mc^{n + m} | n, m \in \mathbb{Z}, n \geq 0, m \geq 0\}$$
では、始めていこう。
まず手順1、今\(B \rightarrow \varepsilon\)があるのでこれを変換していく。
\(B\)を生成先に持つ生成規則は以下二つだ。
- \(S \rightarrow B\)
- \(B \rightarrow bBc\)
よって、それぞれからこの\(B\)を取り除いた以下二つの生成規則を加える。
- \(S \rightarrow \varepsilon\)
- \(B \rightarrow bc\)
そして、\(B \rightarrow \varepsilon\)を削除し、以下5つとなる。
- \(S \rightarrow aSc\)
- \(S \rightarrow B\)
- \(S \rightarrow \varepsilon\)
- \(B \rightarrow bBc\)
- \(B \rightarrow bc\)
このとき、置き換え元は削除していなかったことに注意してほしい。
これで、生成先が\(\varepsilon\)であるような生成規則が開始記号からの\(S \rightarrow \varepsilon\)のみになったので完了だ。
次に手順2…については、今は削除するものはない。
気になる方は、実際に確認してもらえればと思う。
では、手順3に移ろう。
今、単一規則は\(S \rightarrow B\)のただ一つ。
よって、以下二つを加え、この単一規則を削除する。
- \(S \rightarrow bBc\)
- \(S \rightarrow bc\)
この結果、生成規則は以下6つになる。
- \(S \rightarrow aSc\)
- \(S \rightarrow bBc\)
- \(S \rightarrow bc\)
- \(S \rightarrow \varepsilon\)
- \(B \rightarrow bBc\)
- \(B \rightarrow bc\)
次の手順4、終端記号についてだ。
今回は終端記号が3つあるので、以下3つの生成規則を加えよう。
- \(X_a \rightarrow a\)
- \(X_b \rightarrow b\)
- \(X_c \rightarrow c\)
これを使って置き換え、以下9個になる。
- \(S \rightarrow X_aSX_c\)
- \(S \rightarrow X_bBX_c\)
- \(S \rightarrow X_bX_c\)
- \(S \rightarrow \varepsilon\)
- \(B \rightarrow X_bBX_c\)
- \(B \rightarrow X_bX_c\)
- \(X_a \rightarrow a\)
- \(X_b \rightarrow b\)
- \(X_c \rightarrow c\)
最後の手順5、長さが3以上の変数列は以下二つ。
- \(X_aSX_c\)
- \(X_bBX_c\)
ということで、これも以下二つの生成規則を加えよう。
- \(Y_1 \rightarrow SX_c\)
- \(Y_2 \rightarrow BX_c\)
これで置き換え、最終的に以下11個が生成規則となる。
- \(S \rightarrow X_aY_1\)
- \(S \rightarrow X_bY_2\)
- \(S \rightarrow X_bX_c\)
- \(S \rightarrow \varepsilon\)
- \(B \rightarrow X_bY_2\)
- \(B \rightarrow X_bX_c\)
- \(X_a \rightarrow a\)
- \(X_b \rightarrow b\)
- \(X_c \rightarrow c\)
- \(Y_1 \rightarrow SX_c\)
- \(Y_2 \rightarrow BX_c\)
以上で完了だ。
おわりに
今回は、チョムスキー標準形という内容を扱った。
まだ不安な方は、他にも幾つか具体例を通して変換方法などを確認しておこう。
ちなみに、手順内で紹介した余分な生成規則の削除は今回に限らず常に使える。
無駄な定義が入っているように感じたら、この方法で削減してみよう。
さて、次回はもう一つの標準形であるグライバッハ標準形について解説していく。
変換方法もご紹介するが、その時はチョムスキー標準形から出発するので、今回の内容もしっかり復習してから進んでいこう。
2021/2/3追記
次回の、グライバッハ標準形を解説した。
ちょっと予定が変更になり、出発点はチョムスキー標準形である必要がなくなった。
手順がそこそこ複雑なので、具体例を幾つか試しながら進めてもらいたい。



コメント