本シリーズでは、以下の本に沿って解説を書いている。
前回は、\(uvwxy\)定理、あるいは反復補題と呼ばれる内容を解説した。
これを使えば、全てではないがある言語が文脈自由言語でないことを示せるようになる。
幾つか具体的に練習して、使えるようにしておきたい。
以下がその記事だ。
さて、今回は参考書で言うと新しい章に入る。
以前もオートマトンを幾つか解説していたが、その系統で新しいオートマトンが出てくる。
その名も、プッシュダウンオートマトン。
…といきたいところなのだが、実は参考書の内容は、制限付きになっている。
しかし、一般的にはその制限はついていないもので扱われているので、そちらに合わせて内容をちょっと変更させてもらう。
詳しくは、本記事の後半で触れることにしよう。
スタック
さて、プッシュダウンオートマトンに入る前に、このスタックという考え方を紹介しなければならない。
スタックというと、通常はデータ構造で出てくるものを思い浮かべるかもしれないが、おおむねそのままで問題ない。
今回のプッシュダウンオートマトンに出てくるスタックは、スタック記号という通常の記号とは異なるものを一時的に格納することができる補助的な記憶装置だ。
そして、それには以下3つの操作のみが許されている。
- 先頭の記号が何かを確認する ※スタックの中身は変化しない
- 先頭に、記号を一つ追加する(プッシュ)
- 先頭から、記号を一つ取り除く(ポップ)
例えば、スタック記号が\(A\)と\(B\)の二種類で、今スタックに上から\(A\)、\(B\)、\(B\)という順番で記号が入っていたとする。
図にすると、以下のような感じだ。
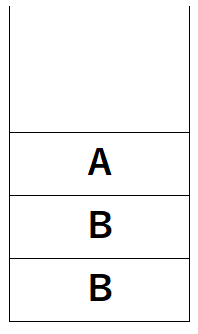
このとき、まず一番上に入っている記号が\(A\)だと確認するのは問題ない。
あるいは、その\(A\)の上に\(A\)や\(B\)を追加することができたり、逆に先頭の\(A\)を取り除くことも可能だ。
しかし、今3つの記号が入っているという情報や一番下に\(B\)が入っているという情報を取得したり、一番下に\(A\)を追加したりといった操作はできない。
不透明で、高さが分からない筒に入っているところを想像してもらうといいだろう。
ちなみにだが、スタックに何も入っていない時に限り、その何も入っていないという情報は取得できる、と考えることもできる。
まあ、先頭を見ようとしてもその先頭が無いので、それで判断できる、というイメージだ。
こんなスタックというものを使って、プッシュダウンオートマトンを定義していく。
プッシュダウンオートマトン
ここから本題だ。
先に、非常に簡単ではあるがイメージだけお伝えしよう。
これは、以前やったnfa(非決定性有限オートマトン)に上で解説したスタックを導入したような考え方になる。
つまり、結局は記号列がある言語に入っているかを確認するための機械だと思ってもらっていい。
nfaの時と同じように状態遷移をすることができるのと、プラスでスタックへの操作も同時に可能になっている。
そんなことを頭の片隅に入れつつ、このプッシュダウンオートマトンを定義していこう。
プッシュダウンオートマトン(以降、pdaと呼ぶ)は、以下6つの組で表される数学的モデルだ。
- \(K\) : 状態の有限集合
- \(\Sigma\) : 入力記号の有限集合
- \(\Gamma\) : スタック記号の有限集合
- \(\delta\) : 状態遷移関数(詳細は後述)
- \(s_0\) : 初期状態(\(s_0 \in K\))
- \(Z_0\) : スタック初期記号(\(Z_0 \in \Gamma\))
\(\Gamma\)は、\(\gamma\)(読み:ガンマ)の大文字だ。
この6つの組で、例えば\(M = (K, \Sigma, \Gamma, \delta, s_0, Z_0)\)と書かれる。
状態と入力記号はnfaの時と同じ。
スタック記号は、上で解説したスタックの中に入れる専用の記号になっている。
本記事では分かりやすいように、基本的に小文字が入力記号、大文字がスタック記号で表すことにしよう。
また、この開始時にはスタックに\(Z_0\)という特殊なスタック記号一つが入った状態で開始される、というイメージだ。
さて、状態遷移関数がちょっと複雑。
これは、先に式で書くと以下のような対応になっている。
$$K \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow 2^{K \times \Gamma^*}$$
言葉で説明すると、まず関数の出発点は三つの組。
ある状態から記号を読み取るのだが、同時にスタックの先頭に何が入っているかも確認する。
この三つの情報を元に、次状態と今あったスタックの先頭をどう変化させるか、という内容を状態遷移関数で定義することになる。
そして、非決定性なので、次の組が複数あったり、あるいはなくてもいい。
定義がべき集合になっているのは、それが理由だ。
入力記号のところには空列\(\varepsilon\)が入ってもいいとしているが、ここが参考書と異なる点になる。
これを許すことでどうなるかは後半でお見せしよう。
例えば、今ある状態\(s\)にいて、記号\(a\)を読み込みたいとする。
このとき、スタックの先頭が\(A\)なら、状態はそのままでスタックの先頭にさらに\(A\)を追加したい、という状況を考える。
このときは、以下の式が成り立つことになる。
$$(s, AA) \in \delta(s, a, A)$$
注意としては、スタックの先頭の文字を入れ替えるように記述するという書き方になっていること。
もう一つ、現状態と記号は同じく\(s\)と\(a\)で、今度はスタックの先頭が\(B\)だったら、状態を\(s’\)に変えて、先頭の\(B\)を削除したいとする。
このときは以下の通りだ。
$$(s’, \varepsilon) \in \delta(s, a, B)$$
最初は戸惑うかもしれないが、何回もやって慣れていこう。
さて、ここで一つ補足を。
スタックの説明のところでは、先頭の確認、先頭へのプッシュ、先頭からのポップの三つの操作しか許されていないと書いた。
しかし、状態遷移関数の定義方法は先頭を入れ替えるようになっているが、問題ないのだろうか、という点。
これは、問題がない。
状態遷移関数の書き方を3パターンに分けて考えてみよう。
まず、遷移先のスタック記号列が空列の場合。
この時は、先頭の記号を削除するような動きなので、動作で言うとポップのみとなり問題ない。
次に、遷移先のスタック記号列が、元の先頭と同じだった場合。
これは、何もしないのと同じなので問題ないことは明らかだろう。
最後、遷移先のスタック記号列が上以外の場合。
例えば、遷移先のスタック記号列が\(ABB\)となっていたとしよう。
この時は、まず元の先頭を一回ポップで削除する。
その後、\(B\)、\(B\)、\(A\)の順番でプッシュすることで実現できる。
このように、一回の状態遷移でスタックからポップできるのは最初だけで回数は最大でも1回だが、その後はプッシュを何回でも行える、と考えるといいだろう。
また、式でスタックの中身を書く時は左が先頭側、右が底側になるのでこれも注意だ。
…さて、ここまで基本的な事項を定義してきたが、もう少し定義するものがある。
具体例はその後にお見せすることにしよう。
pdaの様相
以前も定義していたが、このpdaでも様相というものを考える。
pdaにおける様相とは、状態、入力記号列、スタック記号列の3つの組のことだ。
状態\(s \in K\)、入力記号列\(x \in \Sigma\)、スタック記号列\(\alpha \in \Gamma^*\)を使って、以下のように書き表す。
$$(s, x, \alpha)$$
これは、その時点での読み込みとスタックの状況を表していると捉えられる。
例えば、以下の様相。
$$(s_1, aabb, AB)$$
これは、今状態\(s_1\)にいて、残り\(aabb\)という列を読み込みたく、さらにスタックは上から\(A\)、\(B\)の順番でスタック記号が入っている、という見方ができる。
次のステップを見た方がより実感が湧きやすいだろう。
pdaのステップ
ということで、そのステップを定義していく。
今、pda\(M = (K, \Sigma, \Gamma, \delta, s_0, Z_0)\)において以下二つの様相を考える。
- \(C_1 = (s, ay, A\beta)\)
- \(C_2 = (s’, y, \alpha \beta)\)
ただし、\(s, s’ \in K\)、\(a \in \Sigma \cup \{\varepsilon\}\)、\(y \in \Sigma^*\)、\(A \in \Gamma\)、\(\alpha, \beta \in \Gamma^*\)だ。
これについて以下の式が成り立つとき、様相\(C_1\)から様相\(C_2\)へ、1ステップで変わりうると定義する。
$$(s’, \alpha) \in \delta(s, a, A)$$
要するに、状態遷移関数を一回使って変化できるような様相について、1ステップで移れるということだ。
状態遷移関数の定義では、状態\(s\)にいて入力記号\(a\)を読む場合についてスタックの先頭が\(A\)なら、状態が\(s’\)に変わってスタックの先頭が\(\alpha\)へと置き換わる、ということを表している。
様相を見ると、状態が\(s\)から\(s’\)へ、入力記号は先頭の\(a\)を読むのでそれが消えており、さらにスタックの先頭である\(A\)が\(\alpha\)という列に変わっている、と捉えられるだろう。
また、記号も以前のものと同じく…
$$C_1 \Rightarrow C_2$$
と表記する。
ここも参考書と少し変えており、参考書では\(a\)について空列を許していない。
が、上でも状態遷移関数の入力記号部分に空列を許したことで、こちらもそうなっている。
これを使って、複数のステップも定義しよう。
ある二つの様相\(C_1\)、\(C_n\)について、以下のようなステップが存在するとき、\(C_1\)から\(C_n\)へは何ステップかで変わりうると定義する。
$$C_1 \Rightarrow C_2 \Rightarrow … \Rightarrow C_n$$
もちろん、\(C_1 \Rightarrow C_n\)でも、もっと言うと\(C_1 = C_n\)でもOKだ。
また、表記もこれまでと同じく…
$$C_1 \overset{*}{\Rightarrow} C_n$$
とする。
pdaが受理する列と認識する言語
定義の最後はこれらだ。
pda\(M = (K, \Sigma, \Gamma, \delta, s_0, Z_0)\)と列\(x \in \Sigma^*\)について、以下のステップが存在するとき、列\(x\)はpda\(M\)で受理されると定義する。
$$(s_0, x, Z_0) \overset{*}{\Rightarrow} (s, \varepsilon, \varepsilon)$$
要するに、入力記号列を読んでいき、読み終えた時点でスタックの中身が空になれば、その列は受理される、という定義だ。
なお、このステップ後の様相\((s, \varepsilon, \varepsilon)\)を特に受理様相と呼ぶこともあるので覚えておこう。
そして、pda\(M\)で受理される列\(x\)の集合が、pda\(M\)が認識する言語、となる。
さて、ここまで色々と定義をしてきたが、これだけだと具体的な使い方がイマイチ分からないと思う。
そこで、幾つか具体例を見ていこう。
pda具体例その1
一つ目に、以下の言語を認識するpdaを見てみよう。
$$L = \{xcx^R | x \in \{a, b\}^*\}$$
前半は\(a, b\)からなる列があり、\(c\)が出てきたら先ほどの\(a, b\)の列と逆になった列が並ぶ、という列を含んでいる。
例えば、\(c\)、\(abcba\)、\(aabacabaa\)、などなど。
結論だけ出してしまうが、これを認識するpda\(M = (K, \Sigma, \Gamma, \delta, s_0, Z_0)\)は以下のようになる。
- \(K = \{s_0, s_1\}\)
- \(\Sigma = \{a, b, c\}\)
- \(\Gamma = \{A, B, Z_0\}\)
状態遷移関数は、対応先が空集合でないものだけ書くと以下の通り。
- \(\delta(s_0, a, Z_0) = \{(s_0, A)\}\)
- \(\delta(s_0, b, Z_0) = \{(s_0, B)\}\)
- \(\delta(s_0, c, Z_0) = \{(s_1, \varepsilon)\}\)
- \(\delta(s_0, a, A) = \{(s_0, AA)\}\)
- \(\delta(s_0, b, A) = \{(s_0, BA)\}\)
- \(\delta(s_0, c, A) = \{(s_1, A)\}\)
- \(\delta(s_0, a, B) = \{(s_0, AB)\}\)
- \(\delta(s_0, b, B) = \{(s_0, BB)\}\)
- \(\delta(s_0, c, B) = \{(s_1, B)\}\)
- \(\delta(s_1, a, A) = \{(s_1, \varepsilon)\}\)
- \(\delta(s_1, b, B) = \{(s_1, \varepsilon)\}\)
今後も、具体的に状態遷移関数を書いたときには、断りがなければ省略したものの対応先は全て空集合であるとしよう。
さて、実際に列を受理するかどうかの判断をやってみよう。
上で書いたように、受理様相までのステップが存在するかを見ることになる。
まず、\(abcba\)という列について。
最初の様相は、\((s_0, abcba, Z_0)\)となっている。
このとき辿れるステップとしては、状態\(s_0\)、記号\(a\)、スタック記号\(Z_0\)による状態遷移なので一番上のものが使える。
これを使って1ステップ進めると…
$$(s_0, abcba, Z_0) \Rightarrow (s_0, bcba, A)$$
こんな感じになる。
このまま続けてみよう。
$$\begin{eqnarray}
(s_0, abcba, Z_0) & \Rightarrow & (s_0, bcba, A) \\
& \Rightarrow & (s_0, cba, BA) \\
& \Rightarrow & (s_1, ba, BA) \\
& \Rightarrow & (s_1, a, A) \\
& \Rightarrow & (s_1, \varepsilon, \varepsilon)
\end{eqnarray}$$
このように、最後に受理様相までステップで辿ることができた。
よって、列\(abcba\)は\(M\)で受理される、と言うことができる。
よりイメージを掴みやすくするため、スタックと状態の変化の様子を図にしてみよう。
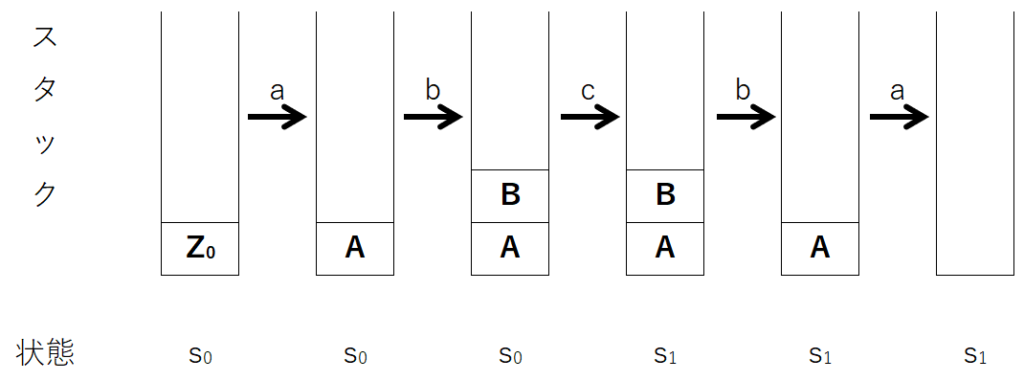
こう見れば、動作が分かりやすいと思う。
もう一つ、参考書にも載っている列\(abaaacaaaba\)をやってみる。
流れは同じなので、ステップの様子だけ見せることにしよう。
$$\begin{eqnarray}
(s_0, abaaacaaaba, Z_0) & \Rightarrow & (s_0, baaacaaaba, A) \\
& \Rightarrow & (s_0, aaacaaaba, BA) \\
& \Rightarrow & (s_0, aacaaaba, ABA) \\
& \Rightarrow & (s_0, acaaaba, AABA) \\
& \Rightarrow & (s_0, caaaba, AAABA) \\
& \Rightarrow & (s_1, aaaba, AAABA) \\
& \Rightarrow & (s_1, aaba, AABA) \\
& \Rightarrow & (s_1, aba, ABA) \\
& \Rightarrow & (s_1, ba, BA) \\
& \Rightarrow & (s_1, a, A) \\
& \Rightarrow & (s_1, \varepsilon, \varepsilon)
\end{eqnarray}$$
これで完了だ。
是非、状態遷移関数と見比べてどう変化させているかも見ておいて欲しい。
さて、受理されない列を入力するとどうなるか、見てみよう。
まず、\(abba\)という列。
\(c\)がないので、言語に含まれないのは明らかだ。
では、ステップを辿ってみる。
$$\begin{eqnarray}
(s_0, abba, Z_0) & \Rightarrow & (s_0, bba, A) \\
& \Rightarrow & (s_0, ba, BA) \\
& \Rightarrow & (s_0, a, BBA) \\
& \Rightarrow & (s_0, \varepsilon, ABBA)
\end{eqnarray}$$
この時点で、列を全て読み終えてしまった。
しかし、スタックがまだ空になっていないので、この列\(abba\)は受理されない、ということになる。
もう一つ、今度は\(abcbaa\)で見てみる。
$$\begin{eqnarray}
(s_0, abcbaa, Z_0) & \Rightarrow & (s_0, bcbaa, A) \\
& \Rightarrow & (s_0, cbaa, BA) \\
& \Rightarrow & (s_1, baa, BA) \\
& \Rightarrow & (s_1, aa, A) \\
& \Rightarrow & (s_1, a, \varepsilon)
\end{eqnarray}$$
今度は、列を読み終えるまでにスタックが空になってしまった。
さて、ここで状態遷移関数の定義を思い出してほしい。
状態遷移関数の出発点は、現状態、一つの入力記号もしくは空列、一つのスタック記号だった。
つまり、先にスタックが空になってしまうと、その置き換え元を用意することができない。
言い換えるとそこから先のステップを作り出すことができないので、これも受理されないと判断できる。
ここまでは参考書通りだ。
また、各遷移先がただ一つなので、まだ分かりやすい。
では、次はそうでないような例を見てみよう。
pda具体例その2
今度は、以下の言語を認識するpdaを考える。
$$L = \{xx^R | x \in \{a, b\}^*\}$$
参考書と微妙に違うことに気を付けよう。
基本は同じで、\(a, b\)からなる列が前半にあり、後半は前半を逆にした列が続く。
しかし、参考書では空列を許していなかったが、こちらは空列でもOKとなっている。
これで参考書の定義だとどうなっていたかお分かりだろう。
実は、参考書の定義(状態遷移関数の入力記号に\(\varepsilon\)を許さない定義)だと、空列を受理することができなくなる。
このとき、入力記号を読まずに遷移することができない。
つまり、空列を入力するとどう頑張っても受理様相までのステップを…もっと言うと、ステップ自体作り出すことが不可能になる。
一般的にはやはり空列も考えた方がいいと思ったので修正させてもらった、というわけだ。
…話を戻して、上に出した言語\(L\)を認識するpda\(M = (K, \Sigma, \Gamma, \delta, s_0, Z_0)\)を作ると以下の通り。
- \(K = \{s_0, s_1\}\)
- \(\Sigma = \{a, b\}\)
- \(\Gamma = \{A, B, Z_0\}\)
この状態遷移関数内訳は以下だ。
- \(\delta(s_0, \varepsilon, Z_0) = \{(s_1, \varepsilon)\}\)
- \(\delta(s_0, a, Z_0) = \{(s_0, A)\}\)
- \(\delta(s_0, b, Z_0) = \{(s_0, B)\}\)
- \(\delta(s_0, a, A) = \{(s_0, AA), (s_1, \varepsilon)\}\)
- \(\delta(s_0, a, B) = \{(s_0, AB)\}\)
- \(\delta(s_0, b, A) = \{(s_0, BA)\}\)
- \(\delta(s_0, b, B) = \{(s_0, BB), (s_1, \varepsilon)\}\)
- \(\delta(s_1, a, A) = \{(s_1, \varepsilon)\}\)
- \(\delta(s_1, b, B) = \{(s_1, \varepsilon)\}\)
参考書からの変更点は、一つ目の空列による遷移を追加した部分のみ。
先ほどと同じく、この9個以外の組合せは全て空集合への対応になることも気を付けよう。
これで、列を読み込んでみる。
まずは\(abba\)について、これは言語の定義を見ると\(x = ab\)とすれば\(xx^R\)と書き表すことができるので、言語に含まれている。
では、ステップを考えてみよう。
$$\begin{eqnarray}
(s_0, abba, Z_0) & \Rightarrow & (s_0, bba, A) \\
& \Rightarrow & (s_0, ba, BA) \\
& \Rightarrow & (s_0, a, BBA) \\
& \Rightarrow & (s_0, \varepsilon, ABBA)
\end{eqnarray}$$
なんと、入力記号列が\(\varepsilon\)なのにスタックが残ってしまったので、この列は受理されないとなってしまった。
…ではなく、実は以下のようなステップも存在する。
$$\begin{eqnarray}
(s_0, abba, Z_0) & \Rightarrow & (s_0, bba, A) \\
& \Rightarrow & (s_0, ba, BA) \\
& \Rightarrow & (s_1, a, A) \\
& \Rightarrow & (s_1, \varepsilon, \varepsilon)
\end{eqnarray}$$
これで受理様相までのステップが存在することが分かったので、列\(abba\)は受理される、と判断できるのだ。
このように、状態遷移関数で遷移先が複数あった場合は、そのいずれかを選択し、最後に一つでも受理様相に辿れるようなステップがあれば、その列は受理される、と言うことができる。
ステップ自体は両方とも問題なく辿ることができ、そのうち一つでも受理様相になればその列は受理される、ということを覚えておこう。
nfaの時も受理状態までの遷移が一つでもあればOKだった、というのと同じだ。
では、問題の空列\(\varepsilon\)を入力した時なのだが、追加した一つ目の状態遷移の定義を使えば…
$$(s_0, \varepsilon, Z_0) \Rightarrow (s_1, \varepsilon, \varepsilon)$$
というステップが存在するので、これも問題なく受理できる。
ちなみに、簡単ではあるがこれで本当に意図通りの言語を認識できるか説明してみよう。
なお、参考書の内容は正しい…つまり状態遷移関数の先頭一つが無い時は、\(L \setminus \{\varepsilon\}\)を認識するとさせてもらう。
ここで、スタック初期記号\(Z_0\)と最初のステップに着目する。
最初のステップに使う状態遷移関数の定義は以下いずれかだ。
- \(\delta(s_0, \varepsilon, Z_0) = \{(s_1, \varepsilon)\}\)
- \(\delta(s_0, a, Z_0) = \{(s_0, A)\}\)
- \(\delta(s_0, b, Z_0) = \{(s_0, B)\}\)
これで、空列を入力した時は上に書いた通りで受理されるので問題ない。
では、空列以外を入力したとしよう。
すると、一つ目の内容を使ってしまうと列が残っているのにスタックが空になってしまうので、これは使えない。
つまり、二つ目か三つ目を使うことになるのだが、この時点でスタックから\(Z_0\)が消え、その後も出てこない。
そして、追加した内容はスタックの先頭が\(Z_0\)の場合のみ使われるので、それ以降は使われず、それ以外の定義のみが使われることになる。
ということで、空列以外の時には一つ目の内容は影響しなくなるので、綺麗に認識する言語に空列だけ追加できた、というわけだ。
おわりに
今回は、プッシュダウンオートマトンというものを解説した。
参考書から少し変えさせてもらったが、今後も今回定義した内容で進めていくことにしよう。
ちなみにだが、実はこれでもまだ一般的な定義とは少し違うものになっている。
が、今回の定義でも問題ない。
そのことについては今の段階でやっても混乱してしまうと思うので、少し進めて慣れてきた頃に触れることにする。
参考書にできるだけ近づけた結果、今回の定義になった、というわけだ。
というわけで、次回はそのまま次に進んでいこう。
今回の内容である程度定義や使い方は解説したが、じゃあどうやってこれを作るか、という問題が生じてくる。
そこで、次回はそのpdaの設計方法を紹介していこう。
2021/2/9追記
次回の、pdaの設計を解説した。
…のだが、最悪ここではguessが何を意味しているかだけ把握してもらえれば十分だ。
実際にpdaも作ってみたがかなり複雑なので、最悪分からなければそこは読み飛ばしてしまおう。



コメント