唐突だが、電卓を作りたくなった。
作り方はいくつかあるだろう。
これまで私が講座を幾つか書いていた、プログラミングでももちろん作れる。
だが、それだと単に数字や演算を受け取り、計算させて結果を表示するだけで完成し、簡単すぎてつまらない。
ということで、今回から論理回路というものを使って電卓を作り上げようと考えている。
なんで論理回路かというと…電卓を作りたい場所が、とあるゲームの中なのだ。
その中でこの論理回路を実現できそうだったから、これにした。
正直、やりたいなぁと思いながらこれを書き始めているような状態なので、もしかしたら他にも何か必要な知識等があるかもしれないが…それはその時に考えよう。
ようは見切り発車で新シリーズを始めていることはご了承願いたい。
また、このことから分かると思うが、講座系に入れてはいるものの、実態は勉強結果だ。
一応過去に大学で習ったことはあるのだが…もう何年も前の話で、だいぶ忘れていることが多い。
調べながら書いているが、この内容が合っていると保証するものではないので、そこも注意しつつ読み進めてもらえると幸いだ。
今回は、まずそもそも論理回路とは何ぞやという部分を解説していこう。
そして、最も基本となる3つの回路を解説していく。
最後に、この論理回路を分かりやすく表現するための、論理回路図というものを紹介して終わりにしよう。
論理回路とは?
さて、論理回路というと少し小難しいイメージがあるかもしれない。
基盤があり、それに銅線などを繋いで回路を作っているところを想像する方もいるだろう。
まあ、これは初めて聞いた時の私のイメージなのだが…それはいい。
実体はそんなことはなく、論理回路とはWikipediaで以下のような解説がされている。
真理値の「真」と「偽」、あるいは二進法の「0」と「1」を、電圧の正負や高低、電流の方向や多少、位相の差異、パルスなどの時間の長短、などで表現し、論理素子などで論理演算を実装する。電圧の高低で表現する場合それぞれを「H(ハイ)」「L(ロー)」等という。基本的な演算を実装する論理ゲートがあり、それらを組み合わせて複雑な動作をする回路を構成する。
論理回路 – Wikipedia
…これだとよく分からないので、もっと簡単にしよう。
誤解を恐れずに言うと、「2択の入力を幾つか受け取って、いろんな計算をしよう」というのが論理回路だ。
2択というのは、簡単に言ってしまうとYES、NOのこと。
この2択のことをプログラミングではよく真偽値などと呼ぶが、論理値とも呼び、これが名前になっているのだろう。
…今度は簡単にしすぎただろうか、具体例を見ると実感が湧くと思う。
例えば、家に帰ってきた時を想像してみよう。
靴を脱ぎ、廊下の電気のスイッチを入れると思う。
もちろん、廊下の電気がつく。
そして廊下を通り、リビング等に入る時に、そこにも廊下の電気スイッチがあり、それを操作すると電気が消える。
これも、論理回路の一つとして見なすことができる。
まず、電気スイッチはON、OFFの2択だろう。
これを、玄関側、あるいはリビング側から操作することができる、つまり2つの2択の入力がある。
片方を操作すると電気がつき、もう一度(一回目と同じか別かを問わず)片方を操作すると電気が消えるという出力になっている。
これが、恐らく身近で最も簡単な論理回路の例だと思う。
他に身近な例でいくと、今この記事をご覧いただくために使っているパソコン、あるいはスマートフォン。
これらも、この論理回路を使って作ることが可能だ。
…とはいえ、これはあまりに高度すぎるので、このシリーズではそこまで解説することはできない。
で、タイトルにもある電卓、これも論理回路で作ることができる。
このシリーズの目標は、この電卓を論理回路で作成することだ。
基本的な3つの回路
早速ではあるが、論理回路ではどのような考え方を使うかを見てみよう。
今回は、最も基本となる3つの回路について見ていく。
AND
一つ目はANDというもの。
二つの入力を受け取り、一つの出力を行う。
イメージとしては、ON/OFFのスイッチが二つあり、ある条件を満たすとランプがつくところを想像してもらうといいだろう。
で、このAND回路は、二つのスイッチが両方ともONだった場合のみランプが点灯する。
入力の組合せを全て表で書くと、以下の通りだ。
| スイッチ1 | スイッチ2 | ランプ |
|---|---|---|
| OFF | OFF | 消灯 |
| OFF | ON | 消灯 |
| ON | OFF | 消灯 |
| ON | ON | 点灯 |
OR
二つ目はORだ。
一つ目がANDという名前で、両方がONの時にランプがつくことから、なんとなく想像付くかもしれない。
恐らくその想像通りで、これも2つの入力を受け取り、今度はそのどちらか一方でもONであればランプが点灯するような回路だ。
同じく、表にしてみよう。
| スイッチ1 | スイッチ2 | ランプ |
|---|---|---|
| OFF | OFF | 消灯 |
| OFF | ON | 点灯 |
| ON | OFF | 点灯 |
| ON | ON | 点灯 |
NOT
三つ目はNOTというもの。
これは、ANDやORとは異なり、入力は一つのみ。
出力は、入力と逆になる。
そのため、スイッチがOFFの時にランプが点灯し、ONの時は消灯する、という結果になる。
| スイッチ | ランプ |
|---|---|
| OFF | 点灯 |
| ON | 消灯 |
3つの回路の結合
もちろんだが、この3つしかないと表現できる出力は微々たるものだ。
だが、これは組み合わせて使うことができる。
先ほどまでの説明で、スイッチによりランプが点灯、あるいは消灯するように説明した。
このランプの点灯・消灯がその回路の出力で、これをまた別の回路の入力にも使える、ということ。
例えば、三つの入力を受け取り、一つ目と二つ目が同時にONになっている、あるいは三つ目がOFFになっている時にランプを光らせるようなことも可能だ。
今出した例を、実際に考えてみよう。
なお、この論理回路は数式で書くことも可能だ。
軽く、その書き方も同時に見ていこう。
まず、入力となる3つのスイッチを変数\(S_1\)、\(S_2\)、\(S_3\)で表すことにしよう。
この中には0か1が入り、0はスイッチがOFF、1はスイッチがONであることを表す。
次に、ANDは2変数を\(\cdot\)を挟むか何も書かずにつなげる、ORは\(+\)で挟むことで表現する。
例えば\(S_1 + S_2\)と書かれればこれはORになるし、\(S_1S_3\)や\(S_1 \cdot S_3\)はANDを表している。
そして、NOTは上に横棒をつける。
\(\overline{S_1}\)が、\(S_1\)のNOTを表している。
その他、括弧をつけたらその中が優先順位が高く、ANDとORが並んでいたらANDの方が優先順位が高い。
例えば、\(S_1 + S_2S_3\)と書かれていたら、先に\(S_2\)と\(S_3\)のANDを取り、その結果と\(S_1\)のORを取る、という順番だ。
なお、NOTもその横棒が伸びている範囲の中身を先に計算し、その後に反転させるという順だ。
\(\overline{S_1 + S_2} \cdot S_3\)なら、先に\(S_1\)と\(S_2\)をORで取り、その結果を反転させ、それと\(S_3\)のANDを取る、という形になる。
そして、この計算式の結果が0になれば出力が0、1になれば出力が1になる、ということ。
ここまで分かれば、一旦は大丈夫だろう。
さて、ではさっきちらっと出した例を数式で表現してみる。
三つの入力を受け取り、一つ目と二つ目が同時にONになっている、あるいは三つ目がOFFになっている時にランプを光らせる、というものだ。
まず、一つ目と二つ目が同時にONになっている、というのはANDなので、\(S_1S_2\)。
三つ目がOFFというのはNOTなので\(\overline{S_3}\)。
これをORで繋げればいいので…
$$S_1S_2 + \overline{S_3}$$
という形になるのだ。
これが1になった時に、ランプを光らせればいい。
ちなみに、これを表形式で書き表すと以下のようになる。
| \(S_1\) | \(S_2\) | \(S_3\) | ランプ |
|---|---|---|---|
| 0 | 0 | 0 | 点灯 |
| 0 | 0 | 1 | 消灯 |
| 0 | 1 | 0 | 点灯 |
| 0 | 1 | 1 | 消灯 |
| 1 | 0 | 0 | 点灯 |
| 1 | 0 | 1 | 消灯 |
| 1 | 1 | 0 | 点灯 |
| 1 | 1 | 1 | 点灯 |
論理回路図
さて、ここまで色々書いてきたが、言葉や数式だけだと分かりづらいだろう。
そこで、この論理回路を図で表現していこう。
そのまま、論理回路図と呼ぶ。
ここでは、各演算(AND、OR、NOTなど)を一個の図形にし、それを線で繋ぐことで入出力を表現する。
図形を言葉で説明するのは難しいので、3つの演算の図形を出してしまおう。
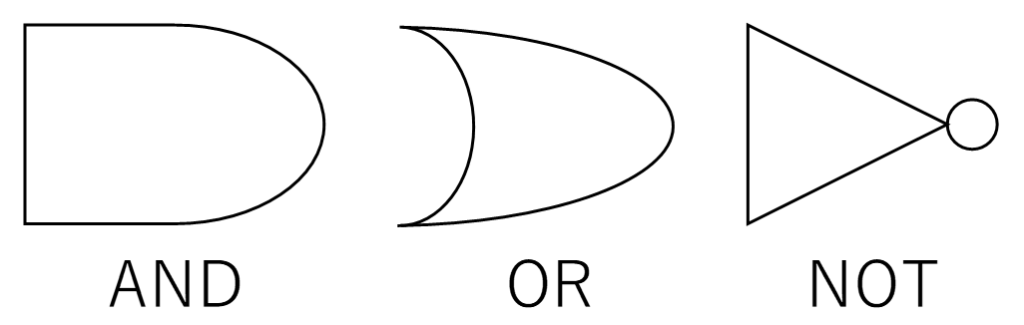
こんな感じだ。
厳密にはORの形が違うような気がするが…Excelで無理やり表現しており、私にはこれが限界だった。
「いや違う、ここは本当はこうなっている」とか突っ込みたい方もいらっしゃるかもしれないが…そこは許してほしい。
正確な形は、是非ご自身で調べていただきたい。
どれも、左側から入力を線でつなぎ、右側に出力を繋ぐ。
これで、先ほどの\(S_1S_2 + \overline{S_3}\)を論理回路図にすると以下のような感じになる。
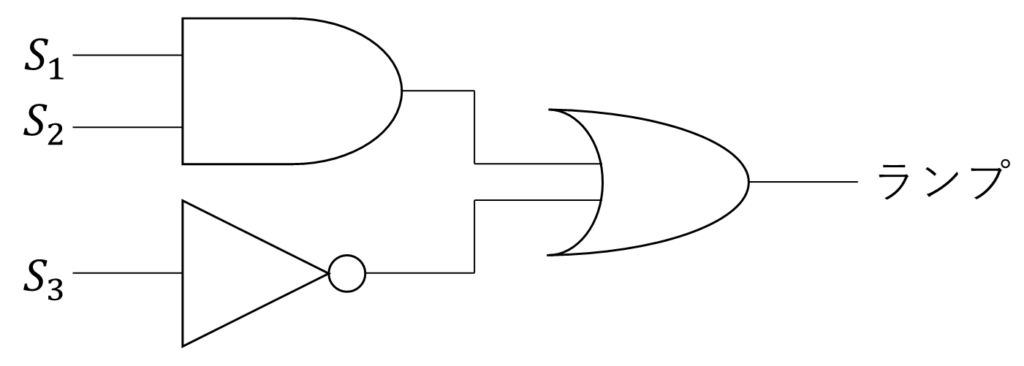
さて、もう一つ、最初の方に出した廊下の電気の例も考えてみよう。
まず、初期状態は両方ともスイッチはOFF、電気もついていない。
これで、片方どちらでもいいのでスイッチをONにすると、電気がつく。
そして、その状態からまた片方のスイッチを切り替えると、電気が消える。
このとき、スイッチ1を先にONにしたと考えてみる。
これでもう一回スイッチ1を操作すると、両方OFFに戻る。
スイッチ2を操作すると、今度は両方ONだ。
…ほんとは厳密に全部見たいが、そこまでやっていると面倒なので結論を出してしまおう。
この回路は、2つの入力について、ONとOFFが異なっていれば電気がつくようになっている。
| スイッチ1 | スイッチ2 | 電気 |
|---|---|---|
| OFF | OFF | 消灯 |
| OFF | ON | 点灯 |
| ON | OFF | 点灯 |
| ON | ON | 消灯 |
さて、2つの入力が異なっていればいいということは、電気がつくパターンは2つだ。
- スイッチ1がOFF、かつスイッチ2がON
- スイッチ1がON、かつスイッチ2がOFF
このどちらかになっていればいいので、数式で表すと以下のようになる。
$$\overline{S_1}S_2 + S_1 \overline{S_2}$$
ということで、これも図にしてみよう。
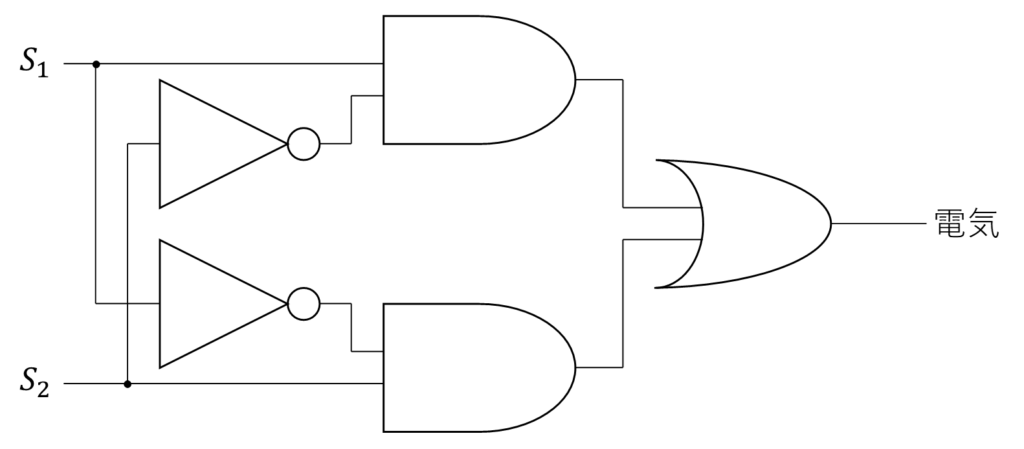
さて、ここで線が交わっているところが3か所あり、うち2か所に黒丸がついている。
この黒丸は、線が分岐することを表しているため、\(S_1\)、\(S_2\)の入力はそれぞれAND、NOTの両方に入力される、と見るようにしよう。
逆に、黒丸がなく単に交わっているところは、互いに影響を与えない。
そのため、\(S_1\)、\(S_2\)からそれぞれNOTに入力しているところの交点は特に何もないので、そこは覚えておこう。
単に、表記上交差してしまっているだけだ。
おわりに
今回は、論理回路とは何かから基本的な3つの回路、そして論理回路図の書き方までまとめた。
このあたりが分かっていないと何もできないので、しっかり把握するようにしたい。
…ちなみにではあるが、今回紹介した3つのAND、OR、NOTの組合せだけで大体の回路を構成することができる。
こんな単純な組み合わせだけなのに、表現できる幅がとても広いのは面白い。
さて、次回はいきなりではあるものの少し横道に逸れて、2進数について解説していこう。
なんの関係があるの?とお思いかもしれないが、これも非常に重要な考え方だ。
特に今回のシリーズの目標である電卓を作る際には計算をする必要があり、そこで2進数の考え方が必須となる。
具体的な関連は後の方で分かると思うが、下準備と思って進めていこう。
2021/11/18追記
ちょっとここに追記するのが遅くなって申し訳ないが、先日次回の内容を更新した。
予定通り、2進数についてだ。
特に、中で紹介している2の補数は非常に重要なので、実際に計算して慣れておくといいだろう。




コメント