本シリーズは、論理回路で電卓を作ろうと思い、そのために勉強した結果を残しているものだ。
前回は、7セグメント表示を題材として、回路を簡略化する手法を二つほど紹介した。
ちょっと、今後楽に進めるため、クワイン・マクラスキー法を行うプログラムも作ってみたいなぁと思っている。
もし作成したら、それも説明と公開をすることとしよう。
まあ、現段階では手で簡略化するので、カルノー図も含めやり方をマスターしておこう。
以下がその記事だ。
さて、今回から個人的に一番面白いところに入る。
これまでは、単に入力のみから出力を決定する組合せ回路を扱っていた。
言い換えれば、今の状態に関わらず、出力が一意に決まる回路だ。
加算器は両方とも入力された2進数の和を出力していたし、7セグメントも今入力されている2進数を10進数表記で表示していただけ。
しかし、本シリーズの目標である電卓には、情報を記憶することが必須となる。
電卓では、まず数字を入力し、演算記号のボタンを押す。
すると一つ目の数字が保持され、二つ目の数字を入力できるようになる。
そこからイコールボタンを押せば、足された結果が表示される、という仕組みだ。
そこで、情報の記憶を行うための順序回路というものに入っていこう。
そして、その順序回路の基本となるフリップフロップというものも解説する。
回路が複雑になってくるが、落ち着いて一個一個確実に進めていこう。
順序回路
さて、冒頭に少し書いてしまったが…順序回路とは現在の入力だけでなく、過去の状態も加味して出力を決定する回路のことだ。
これをすることで、情報の記憶が行えるようになる。
で、過去の状態も考えるということは、出力を再度入力に使いまわすことを表している。
そのため、今後の回路では、出力から分岐して再度別の素子に入力する、という部分が頻発する。
回路図も複雑になってくるので、それぞれの素子に、何が入力されるかをしっかり確認しながら進めていこう。
フリップフロップ
フリップフロップとは、1ビットの情報を保持する順序回路のこと。
ビットというのは2進数における1桁のことで、ようするに0か1を、フリップフロップで記憶することができる。
もちろん、フリップフロップを複数使えば複数の情報を保持することもできる。
これを利用して、実際に電卓を組んでいくことになる。
で、このフリップフロップには4つの代表的な回路があるので、それぞれの詳細を見ていこう。
SRフリップフロップ
一つ目は、このSRフリップフロップというもの。
SとRはそれぞれSet、Resetの略で、指定した入力をそのまま保持することができる。
入力は\(S\)、\(R\)の二つで、出力は\(Q\)、\(\overline{Q}\)の二つ。
ようするに、メインとなる出力と、そのNOTを同時に出力することになる。
論理回路図を以下に示そう。
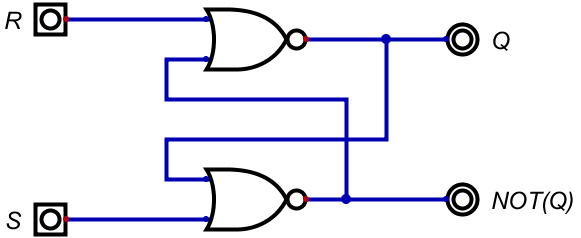
入力が、上が\(R\)、下が\(S\)となっている部分だけ注意。
で、次にこの真理値表(?)を出してみる。
| \(S\) | \(R\) | 次の\(Q\) | 次の\(\overline{Q}\) | 意味 |
|---|---|---|---|---|
| 0 | 0 | \(Q\) | \(\overline{Q}\) | 前の状態を保持 |
| 0 | 1 | 0 | 1 | リセット |
| 1 | 0 | 1 | 0 | セット |
| 1 | 1 | – | – | 禁止 |
さて、これまでの真理値表と色々と異なる。
実は、これは真理値表ではなく、特性表と呼ばれるものだ。
これは、今の入力によって出力される状態がどうなるか、という観点でまとめられた表になる。
順序回路ではこの特性表を使うので、ここで見方もざっと紹介しよう。
まず、入力は真理値表と同じく、0と1の組み合わせを2進数の順番で書いていく。
次に、出力なのだが…順序回路では、今の状態も回路に使用している。
つまり、それが出力に影響するため、表として書く出力は、次の状態という形になる。
そして、その出力の部分にも\(Q\)が入っているが、これは一つ前の状態を表している。
例えば、今\(S\)と\(R\)両方に0が入力された場合、その前の\(Q\)と\(\overline{Q}\)がそのまま出力され続けることを表している。
これで、なんとなく情報を保持するという感覚が分かっただろうか。
次に、\(S\)に0、\(R\)に1が入力されると、前の状態に関係なく\(Q\)は0を出力するようになる。
また、\(S\)に1、\(R\)に0が入力されると、前の状態に関係なく\(Q\)は1を出力。
これで値をセットした状態で両入力を0にすれば、その情報を保持できる、という使い方だ。
さて、今2入力を両方とも1にした場合の出力がハイフンで、意味に禁止と書かれている。
これは、文字通り禁止入力というもので、一応今回出した回路では、前状態に関係なく\(Q\)と\(\overline{Q}\)の両方とも0になる。
が、これは回路の組み方によっては結果が異なり、要するに動作が確定していないのだ。
そういったものに対しては、その入力を禁止してしまおう、ということで禁止入力になっている。
…一応、回路の組み方によってはこの出力も意図したものとして扱える場合があるが、今回はシンプルに禁止として扱おう。
JKフリップフロップ
次に、JKフリップフロップというもの。
このJとKが何の略かは分かっていないらしい。
幾つか説はあるらしいが…まあ、内容には関係ないので飛ばしてしまおう。
これはSRフリップフロップの拡張で、禁止されていた\(S\)と\(R\)ともに1を入力された時の動作も使えるようにしたもの。
論理回路図と特性表を以下に出そう。

先ほどと同じく、名前の順番と入力の上下が逆になっているので注意。
| \(J\) | \(K\) | 次の\(Q\) | 次の\(\overline{Q}\) | 意味 |
|---|---|---|---|---|
| 0 | 0 | \(Q\) | \(\overline{Q}\) | 前の状態を保持 |
| 0 | 1 | 0 | 1 | リセット |
| 1 | 0 | 1 | 0 | セット |
| 1 | 1 | \(\overline{Q}\) | \(Q\) | 前の状態を反転 |
特性表を見てもらえれば分かると思うが、入力が両方とも1の場合以外はSRフリップフロップと同じだ。
両方とも1が入力された時だけ、現在の状態を反転させる、という動作になる。
…勘のいい方ならもしかしたらこの問題点にお気づきかもしれないが、一旦それは後回しにして、次の回路に進もう。
Dフリップフロップ
三つ目は、Dフリップフロップ。
これは入力が1つのみとなり、前の状態に関わらず入力された情報を保持する。
…これだけ書くと、そのまま出力に繋げるのと何が違うの?となりそうだが、それは後で。
このDフリップフロップは、JKフリップフロップ(SRフリップフロップ)の\(J\)(\(S\))にそのまま入力を、\(K\)(\(R\))に入力のNOTを入れてあげれば完成する。
今回はSRフリップフロップを元にして作成しよう。
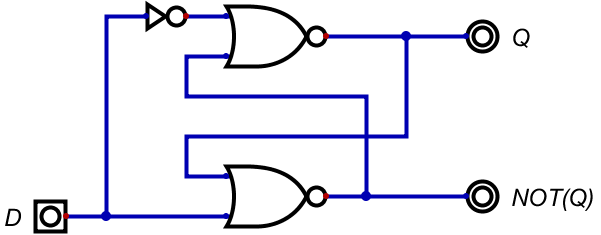
| \(D\) | 次の\(Q\) | 次の\(\overline{Q}\) | 意味 |
|---|---|---|---|
| 0 | 0 | 1 | セット |
| 1 | 1 | 0 | リセット |
ちなみに、DはDelayの略だ。
Tフリップフロップ
最後に、Tフリップフロップ、TはToggleの略。
これも1入力だが、0を入力すると現状態を保持、1を入力すると現状態を反転させるという動作をする。
つまり、JKフリップフロップの両入力に、1つの入力を分岐させて入力するだけで完成だ。
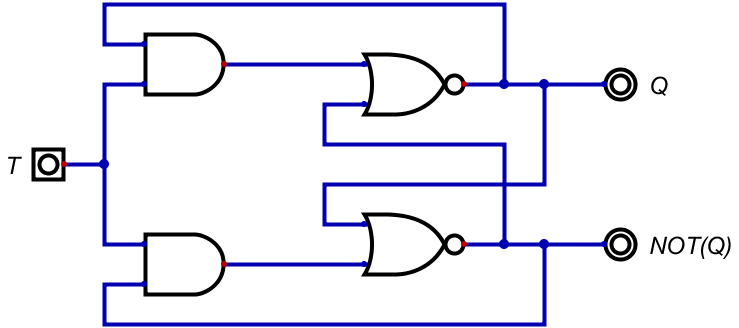
| \(T\) | 次の\(Q\) | 次の\(\overline{Q}\) | 意味 |
|---|---|---|---|
| 0 | \(Q\) | \(\overline{Q}\) | 前の状態を保持 |
| 1 | \(\overline{Q}\) | \(Q\) | 前の状態を反転 |
問題点
さて、今出した4つの回路…のうち、SRフリップフロップを除いた3つの回路には、色々と問題点や謎な点がある。
問題点は、現状態を反転させる部分。
何も考えず、例えばJKフリップフロップで上に出した回路に両方とも1を入力してみよう。
すると、もし現状態が\(Q=0\)だったら、\(Q\)が1に切り替わる。
これで終わればよかったのだが…その変わった\(Q\)、ついでに\(\overline{Q}\)も1から0に変わっており、それらが再度入力される。
すると、それをまた反転させ、今度は\(Q = 0\)、\(\overline{Q} = 1\)となる。
そして、それもまた入力されるので、また反転して…ということを延々と繰り返してしまう。
シミュレータによっては、エラーが出てしまうことだろう。
これは何が原因かというと、今の回路では入力が変化すると、ただちに出力も変化する非同期という形になっていること。
実は問題点はもう一つあり、例えばJKフリップフロップで入力が両方0…つまり、情報を保持しているところから状態を反転させたい、という場合。
このとき、同時に入力を1にしてあげる必要があるのだが、そこにわずかでも時間差があると、現状態が変わってしまう可能性がある。
そして、謎なのがDフリップフロップだ。
上の説明では、やはり入力した内容を素通ししているのと変わらない。
これも、原因は同じく非同期という形で実装されている部分にある。
ではどうするかというと…この出力が変化するタイミングを制御すればいい。
同期とクロック
入力をすぐに出力に反映させるのが、非同期だった。
それに対し、出力に反映させるタイミングを決め、その時点の入力により次の出力を決定するような回路を同期という。
これを使えば、先に入力を変更させておき、反映させてねという入力を入れてあげることにより、そのタイミングで出力を変更させることができる。
つまり、実際にフリップフロップを使う場合には、それぞれにもう一つ入力を入れてあげる必要がある。
そこに入力するのが、クロックと呼ばれる信号。
これは一定周期で0と1を入れ替えながら入力する信号で、これが1の時だけ出力を変化させるようにすれば問題が解決する。
…と思いきや、それでもまだ問題は残る。
やはり、そのクロックが1の間に状態を反転させる場合、何度か状態が入れ替わる可能性がある。
そのため、方法の一つとしては、クロックが1になったときにそこから1回だけ状態を入れ替える、ということをする必要がある。
この方法をマスタースレーブ方式と呼ぶ…が、さらに問題が。
これをする場合、フリップフロップをもう一つ繋げて、後ろの方にはクロックのNOTを入力する。
その後ろのフリップフロップからの出力を、そのフリップフロップの最終的な出力とする。
こうすると…後ろの方は、本来なら変わるはずのタイミングではなく、その次にクロックが0になったタイミングで出力が確定する。
つまり、クロックが1である時間分だけ、出力が遅延するのだ。
今度はそれを解決するために、クロックが0から1になった瞬間のみ入力を出力へ反映させるポジティブエッジトリガという方法がある…のだが、そろそろ頭がクエスチョンマークで埋め尽くされていると思う。
このあたりを詳細に解説しはじめると記事がかなりの長さになりそうなので、次回改めて同期・非同期から解説することにしよう。
おわりに
今回は、順序回路の概要と、非同期の各フリップフロップを解説した。
正直、まだ具体的に動かしていないので、何も感覚が分からないと思う。
また、後半では問題点を解決する方法である同期についても少し触れたが、その詳細は次回解説する。
かなり細かい話になってきて、考えなければいけないことも増えてくるが、一個一個落ち着いて理解していこう。
2021/12/19追記
次回の内容を公開した。
今回問題になっていたものを解決する、同期という形の回路だ。
基本、フリップフロップを使う場合はこの形になると思うので、組み方はともかく…動作をしっかり理解しておこう。





コメント