【連結リスト・ヒープ】高速なソートアルゴリズム前提知識 -データ構造編-

高速なアルゴリズムと呼ばれる以下の3つ。

クイックソート
マージソート
ヒープソート

これらは、直感的には分かりづらい。…なんて、前回と同じ出だしで始めたわけだが。

その理由も前回の冒頭に書いた通り、様々なアルゴリズムとデータ構造を基にした考えだからだ。

で、前回はそのアルゴリズム部分を解説した。

今回は、残るデータ構造部分を解説していこう。

前回の復習
復習：データ構造とは
連結リスト
ヒープ
まとめ：連結リストとヒープ

前回の復習

前回は、主にクイックソート、マージソートに使用される二つの考え方を紹介した。

【再帰・分割統治法】高速なソートアルゴリズム前提知識 -考え方編-

紹介したものは以下二つ。

再帰：ある処理の中で、自分自身を再度呼び出す考え方
分割統治法：大きい問題を、小さい問題に分けて解決する考え方

再帰はアルゴリズムというより単純なプログラムのお話だが、分割統治法は立派なアルゴリズムの一つだ。

今回、またちょっとこれらとは離れるが、次回戻ってくるのでそれまでに理解しておこう。

復習：データ構造とは

そもそも、今までどんなデータ構造が出てきていたのだろうか。

それ以前に、データ構造とは何だったのか。そこから見直しておこう。

データ構造とは、処理するデータをどうやって扱うか、という部分のお話だ。

今までJavaScriptで解説していた変数、配列、オブジェクトを振り返ってみよう。

変数はただ一つのデータ。

配列は、複数のデータを一つの名前＋添え字でアクセス可能にしたデータ。

そしてオブジェクトは、複数のデータそれぞれに名前をつけ、一つのモノとしてまとめたデータ。

これらは、あくまでプログラム上でのデータの保持方法だ。

これらをどう使うか、というのが、データ構造という考え方。

そのうちの一部として、今回解説する連結リスト、ヒープというものがある。

連結リスト

では、まずは連結リストから見ていこう。

連結リストとは

連結リストとは、複数のデータを持つ場合に、一つ一つのデータを以下2つの情報を持つオブジェクトとして保持するデータ構造だ。

データ自身
次のデータへのポインタ

ここで言うポインタとは、JavaScriptの参照渡しのところで解説した住所だ。

図にした方が分かりやすいだろう。

例えば、配列で表すと[5,2,8]というデータを連結リストにすると、以下のようになる。

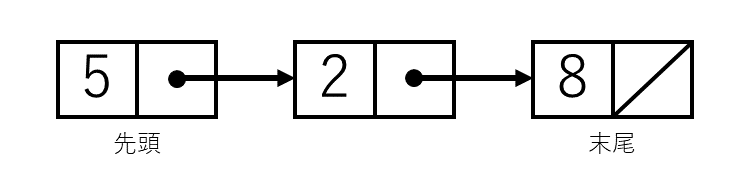
これ全体を、連結リストという。

で、2つの領域を持つ小さい四角が、一つ一つの要素だ。

2つの領域のうち、左側がデータ自身、右側が次のデータへのポインタだ。

先頭へのポインタだけ連結リスト自体に保持しておき、リストの要素へはそこから辿ってアクセスする。

更に、その次へのポインタがない場合に、そこでリストの終了と見なす、といった具合だ。

JavaScriptでの実装例

実装例をお見せしよう。

実際には、この連結リスト全体を表すオブジェクトと、一つ一つの要素を表すオブジェクトを定義する。

クラスで定義してみよう。

class connectList {
    constructor(){
        this.head = null;
    }
}

class connectElement {
    constructor(data){
        this.data = data;
        this.next = null;
    }
}

純粋なパラメータのみ保持する場合だとこんな感じだ。

connectElementオブジェクトには、dataに実際のデータ、nextに次のconnectElementオブジェクトへのポインタが入る。

上の図でいう一個一個の箱がこのconnectElementオブジェクトだ。

で、その全体を表すconnectListオブジェクトは、リストの先頭にあたるconnectElementオブジェクトへのポインタを入れておく。

こうすることで、連結リストが実装できる。

ただ、このままでは扱いづらい。なので、connectListクラスに以下二つのメソッドも定義しておこう。

配列のように、0から始めて指定した番目にある要素を取得する
末尾に新しい要素を追加する

これも実装すると、以下のようになる。

class connectList {
    constructor(){
        this.head = null;
    }
    getElm(i){
        if(this.head == null){
            return null;
        }
        var elm = this.head;
        while(i > 0){
            elm = elm.next;
            i--;
            if(elm == null){
                return elm;
            }
        }
        return elm;
    }
    addElm(data){
        var newElm = new connectElement(data);
        if(this.head == null){
            this.head = newElm;
            return;
        }
        var elm = this.head;
        while(elm.next != null){
            elm = elm.next;
        }
        elm.next = newElm;
    }
}

class connectElement {
    constructor(data){
        this.data = data;
        this.next = null;
    }
}

ちょっと細かく見てみよう。

まず、配列の添え字のように要素を取得するgetElmメソッド。考え方は以下の通り。

headがない…つまり、要素を一つも持たない場合はnullを返す。
headからi回だけ後ろの要素に辿る。
このとき、iよりも要素の数の方が小さい場合は、そこから先に辿れないため、nullを返す。
辿った結果、指していた要素を返す。

これによって、iの数によって以下のような動作になる。

iが0の時、headから0回辿る…つまり、1回も辿らないので、headが返ってくる。
iが1の時、headから1回辿る…つまり、headの次の要素が返ってくる。
iが2の時、headから2回辿った結果が返ってくる。
…

これで、指定した番目の要素を取り出すことができる。

次に、要素を末尾に追加するaddElmメソッド。

追加する要素となるconnectElementオブジェクトを生成する。
headが空の場合、生成したオブジェクトをheadに入れて終了。
nextを持たない要素…つまり、現時点での末尾の要素を取得する。
取得した末尾の要素のnextに、生成したオブジェクトを入れる。

こんな感じだ。

実際に使う例も見ていこう。上の図で出した[5,2,8]を入れてみる。

var arr = [5, 2, 8];

var list = new connectList();
for(var i = 0; i < arr.length; i++){
    var elm = new connectElement(arr[i]);
    list.addElm(elm);
}

これで、上の図のような連結リストを作ることができた。

オマケ：双方向リスト

連結リストでは、ただ次の要素へのポインタのみを持っていた。

これに、一つ前へのポインタも追加したものが、双方向リストだ。

詳細な説明はしないが、一応名前だけ紹介しておく。

ヒープ

次に、ヒープと呼ばれるデータ構造を見ていこう。

…といきたいところだが、このヒープは別のデータ構造を拡張したものだ。

その元となっている構造は、以下の通り。

木構造
半順序木
二分木

一つずつ見ていこう。

木構造

木構造とは、一つ一つの要素に対して、複数の子と0個か1個の親を持つデータ構造。

これは身近に具体例がいくらでもある。例えば、本の内容。

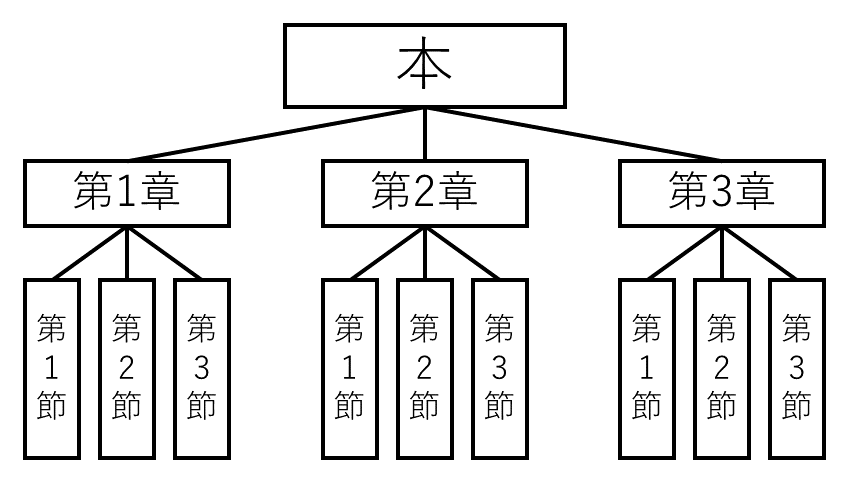
こんなふうに構造化できる。これが木構造だ。

木構造の用語

木構造の特徴の前に、用語を定義してしまおう。

まず、線で結ばれている二つの要素について、下にある要素を上から見て子、上にある要素を下から見て親と呼ぶ。

上の例でいくと、各章は本から見れば子、各節から見れば親だ。

また、親を持たない要素(上の例では本)を根、子を持たない要素(上の例では各節)を葉と呼ぶ。

ある要素について、その親、またその親…というように、上に向かって辿ることのできる要素をまとめて祖先と呼ぶ。

逆に、ある要素の子、またその子…というように、下に向かって辿ることのできる要素をまとめて子孫と呼ぶ。

この木構造では、階層を考えることができる。

根をレベル0として、その直接の子をレベル1、レベル1の要素の子をレベル2、…と考える。

上の例では、本がレベル0、各章がレベル1、各節がレベル2だ。

節に、更に子がいる場合はそれがレベル3となる。

最後に、同じ親を持つ要素同士を、兄弟と呼ぶ。

木構造の特徴

木構造は、以下の特徴を持つ。逆に言えば、以下の特徴を満たす構造を木構造と呼ぶ。

一つの木において、根はただ一つ存在する。
根以外の要素は、必ずただ一つの親を持つ。
全ての要素は、0個以上の子を持つ。

あまり深く追求し始めると別のグラフ理論という分野の知識も必要になってくるので、このあたりにしておく。…グラフ理論も面白いので気になった方は調べてみよう。

とにかく、これらの条件が満たされていれば、それは木構造だ。

この用語や特徴は、これらの拡張である二分木、半順序木、ヒープも共通している。

また、特徴の一つとして、ある要素を新しい根とし、その子孫全てを抜き出した部分もまた木構造になる。

この抜き出した部分を、そのまま部分木と呼ぶ。

半順序木

上では、単純な構造として木構造を定義してきた。

では、ここに三つ特徴を追加しよう。

全ての親は、常に子の要素以下である
全ての葉は、最下層もしくはそれより一つ浅い層に存在する
最下層の葉は、左詰めで配置されている

どういうことかというと、以下のような例だ。

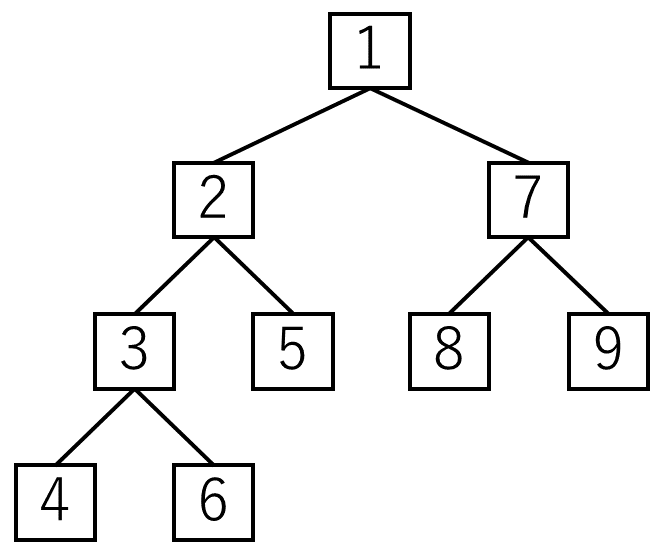
どの親子関係を見てもらっても、必ず親の方が子より小さくなっている。

また、葉のレベルを見てみると…4と6はレベル3、5と8と9はレベル2にある。

更に、レベル3を見ると、左から順番に埋まっている。

このような条件を付け加えた木構造を、特に半順序木と呼ぶ。

この特徴としては、必ず根の要素が最小になる、というものだ。

最終的なヒープでは、この特徴を上手く利用する。

二分木

木構造に、以下の条件を付け加えたものがこの二分木になる。

任意の要素について、子は以下のパターンのいずれかである。
- 0個の子を持つ(子を持たない)
- 1つの子を、左に持つ
- 1つの子を、右に持つ
- 2つの子を、左右に一つずつ持つ

どういうことかというと、最初に出した本の例は、二分木ではない。

葉以外の要素全てが、3つの子を持っているからだ。

では、二分木はどんなものか…というと、半順序木の例がそうだ。

全ての要素が、最大でも二つの子を持っている。

各要素から、多くても二つに分かれている木構造。だから、二分木と呼ぶのだ。

ヒープ

ここまで来て、ようやくヒープの説明に入れる。

ヒープとは、以下の条件を満たす構造のこと。

半順序木である
二分木である

…これだけだ。というわけで、半順序木の例がそのままヒープの例にもなっている。

で、「じゃあこれをどうソートに使うの？」ということだが…これは、次回解説しよう。

これが面白いところで、連結リストがオブジェクトだったのでこちらもオブジェクトになりそうなものだが、実際は配列で表現できる。

配列も使い方を考えるだけで、こんな構造まで表すことができるのだ。

まとめ：連結リストとヒープ

大きく説明したかったのは二つだけなのに、かなり長くなってしまった…

とにかく、今回解説したものをまとめておこう。

連結リスト：以下2つの情報を持つ要素により実現されるデータ構造
- データ
- 次の要素へのポインタ
ヒープ：以下2つの構造を併せ持つ木構造
- 半順序木：以下3つの条件を満たす木構造
  - 全ての親は、常に子の要素以下である
  - 全ての葉は、最下層もしくはそれより一つ浅い層に存在する
  - 最下層の葉は、左詰めで配置されている
- 二分木：全ての要素の子が最大でも2の木構造

前回のアルゴリズムと今回のデータ構造を利用して、やっと次回は高速なソートアルゴリズムを解説できる。

前回、今回の内容を見直しつつ、次回の内容も見てもらいたい。

更新情報はTwitterでも呟いている。よかったら、ページ下部のTwitterアイコンから覗いていってほしい。

それでは。

日	月	火	水	木	金	土
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30