本シリーズは、論理回路で電卓を作ろうと思い、そのために勉強した結果を残しているものだ。
前回は、実際に2進数を入力し、加算と減算を行う回路を作成した。
その中で使用している半加算器、全加算器は重要なので、何をするものだったか、どう作っていたかをしっかり確認しておこう。
以下がその記事だ。
さて、今回も新たに回路を作ってみよう。
タイトルに入れている、7セグメント表示を実装してみる。
今回は、2進数として入力されたものを1桁の10進数として表示するところまで。
この過程で、どのように論理回路を組んでいくか、その簡略化の方法を幾つか見てみよう。
7セグメント表示
そもそもこいつが何者なのか、というところの解説からしていこう。
まず、今回の目標である電卓を思い浮かべて欲しい。
これはスマホの電卓機能とかではなく、よく文房具屋とかで売っている電卓というモノの方。
その数字が表示されるところは、角ばった数字になっていると思う。
他にも、デジタル時計の数字も同じようなものが使われていることが多い。
その表示のことを7セグメントという。
ちょうど、私が使用しているシミュレータにこの7セグメント用出力表示があったので、本シリーズではこれを使わせてもらおう。

7個の細いランプがあり、その点灯している部分を文字として見ると数字になっている、というやつだ。
図には小数点用の点もあるが、今回は無視して7個を扱う。
なぜ今こんな解説をするかというと…今回の電卓の表示に、この7セグメントを使用したい。
その練習として、まずは簡単なもので実装してみよう、という感じだ。
というのと、同時に解説したい回路の簡略化の題材にちょうどいいと思ったからというのもある。
7セグメント表示の実装方法
では、まずは入出力を明確にしておこう。
入力は4個にしておく。
内訳は、4桁の2進数1つだ。
この各桁を、それぞれ1入力として扱う。
そして、出力は1桁の10進数、0から9。
これを、7セグメントとして表示したい。
つまり、7個のランプそれぞれが出力なので、4入力7出力の回路となる。
なお、今回はマイナスを考えず、入力の2進数は10進数表記だと0から15として扱うことにしよう。
入出力の関係
早速、中身を考えていこう。
まずは、入力に対する出力を決めなければいけない。
確認してみたところ、7個のセグメントは上の横棒を1番目、そこから時計回りにぐるっと2番目から6番目、最後に真ん中の横棒が7番目に対応していたので、回路もそのまま\(L_1\)から\(L_7\)として扱う。
それと、今は出力が1桁の10進数なので、入力が\((1010)_2\)以上だと10進数に直した時に2桁になってしまう。
その時は…出力がどうなっていても構わないとしよう。
想定としては、結果の範囲が\((0)_{10}\)以上\((9)_{10}\)以下であるような計算を行い、その結果が今回作る回路に入力される。
それを、7セグメントとしての表示に直すようなことを思い浮かべてもらえればいいだろう。
これを想定すれば、一部の入力は考えずに済む。
ということで、入力の2進数を\(I = I_3 I_2 I_1 I_0\)としたときの、期待する出力\(L_1\)から\(L_7\)の真理値表は以下の通り。
| \(I_3\) | \(I_2\) | \(I_1\) | \(I_0\) | \(L_1\) | \(L_2\) | \(L_3\) | \(L_4\) | \(L_5\) | \(L_6\) | \(L_7\) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | |||||||
| 1 | 0 | 1 | 1 | |||||||
| 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 0 | 1 | |||||||
| 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 |
空欄にしているところは、入力の2進数が\((1010)_2\)以上…つまり、10進数に直すと2桁になってしまうところだ。
さて、これで真理値表が分かったので、あとはゴリゴリ回路を組めば…と思われるかもしれないが、ちょっと待って欲しい。
確かに、このまま回路を組むこともできるのだが…それだと、あまりに効率が悪い。
そこで、なんとかしてこの回路を簡略化…言い換えると、ANDやORなどの基本回路、今更だがこれを素子と呼ぶが…これをなるべく少なくしたい。
そのための考え方を幾つかご紹介…の前に、一つ新たな内容を解説しておこう。
ドントケア
Don’t care.
日本語に直すと、「気にするな」というニュアンスだろう。
先ほど、入力が\((1010)_2\)以上の時は、出力がどうなっても構わないとする、と書いた。
これは、そこを気にしない、という意味でドントケアと呼ばれている。
記号では\(\phi\)(読み:ファイ)をよく使い、ここは0としても1としても扱える。
要するに、先ほどの表で空欄だったところは、これを使うと全て\(\phi\)で埋まっていると考えていい。
これを覚えておくとより簡略化が進むので、この後出す例も交えて確認していこう。
簡略化の方法
では、ここから実際に各入力を簡略化していく。
幾つか方法があるが、7出力のうち幾つかで実際に使いながら解説していこう。
カルノー図
一つ目は、カルノー図と呼ばれるもの。
これは視覚的にも分かりやすい方法で、私もよく使うものだ。
今回の説明では、まず\(L_1\)についてやってみよう。
まず、入出力を表形式でまとめる。
注意点もあるのだが、先にその表だけ出してしまおう。

こんな感じになる。
行、列はそれぞれの入力がどうなっているかを表しており、交差するセルにその結果がどうなっていて欲しいかを記載する。
ポイントは、入力の書く順番だ。
普通なら、00、01、10、11という順番になってそうなところだが、今見ると縦・横両方とも00、01、11、10という順番になっている。
こうなっている理由は後で分かると思うが、簡略化する場合にこの方が都合がいいのだ。
意図としては、隣り合ったセルは、1つの入力しか異ならない、という状態になるようこの順番にしている。
では、ここから簡略化の方法を。
基本的な方針としては、隣接した1を丸で囲っていく。
例えば、1行目の右二つには1が並んでいる。
ここを丸で囲む、というような感じだ。

これで何をしたいか、というのを先に説明しておこう。
まず、これをしない場合、1の個所を表す入力を全てANDで繋いで作っておき、それをORで取っていくという形で回路を作ることになる。
何もしない場合のブール代数形式での出力\(L_1\)を以下に出しておこう。
$$\begin{eqnarray}
L_1 & = & \overline{I_3} \overline{I_2} \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} \overline{I_2} I_1 I_0 \\
& + & \overline{I_3} \overline{I_2} I_1 \overline{I_0} \\
& + & \overline{I_3} I_2 \overline{I_1} I_0 \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & \overline{I_3} I_2 I_1 \overline{I_0} \\
& + & I_3 \overline{I_2} \overline{I_1} \overline{I_0} \\
& + & I_3 \overline{I_2} \overline{I_1} I_0
\end{eqnarray}$$
こんなことになっている。
ここで、今丸で囲った部分だけに注目し、その出力を\(L_1’\)としておこう。
$$L_1′ = \overline{I_3} \overline{I_2} I_1 I_0 + \overline{I_3} \overline{I_2} I_1 \overline{I_0}$$
さて、ここで共通している部分があるので、分配法則を使って抜き出す。
$$L_1′ = \overline{I_3} \overline{I_2} I_1 (I_0 + \overline{I_0})$$
同じ変数に対するそれ自身と否定のORは1になり、1とANDを取っても何も変わらないので…
$$L_1′ = \overline{I_3} \overline{I_2} I_1$$
こう考えることができる。
これを、丸で囲むだけで完成させることができるのだ。
先ほど丸で囲った部分を見てみると、その中では\(I_3 = 0, I_2 = 0, I_1 = 1\)の3つは変わらず、\(I_0\)だけ0と1で変化している。
これは、変わらない3つの変数がその値であれば、残った\(I_0\)に依らずに結果が1になることを意味しているので、そこから\(\overline{I_3} \overline{I_2} I_1\)を求めることができるのだ。
これを利用して簡略化していくのが、カルノー図だ。
先ほど書いた、隣り合ったセルは必ず一つしか違わないようになっているというのは、これをするためのものだ。
なお、この丸は今説明用に2つだけ囲ったが、より大きく囲めばさらに簡略化できそうだ。
丸で囲める時の条件は以下の4つ。
- 囲む領域の中には、1か\(\phi\)のみ入れることができる(0は囲めない)
- 囲む領域は、長方形もしくは正方形
- 囲む領域の大きさ(中に入る1, \(\phi\)の数)は、2の累乗(2, 4, 8, …)
- 表の右と左、上と下は繋がっているとして考えていい
そのため、先ほど囲ったところは、その一行下も含めて、領域数4の正方形で囲むこともできる。

さて、条件内に出してしまっているがここでドントケアについても触れておこう。
ドントケアは先ほど書いた通り、0としても1としても捉えられる。
つまり、今回は今囲った領域の下も全てドントケアなので、1として考えてここまで囲ってしまってOKだ。

ここまで囲めば、\(I_1\)以外は変わっても結果に影響しなくなり、この領域は\(I_1\)だけとなる。
こんな感じで丸を囲っていき、1が全て囲まれればOKだ。
なお、ドントケアは囲っても囲まなくてもいいので、囲まれていないドントケアが残っても問題ない。
囲ったドントケアは1として、囲まれなかったドントケアは0として解釈したことになる。
他のポイントとしては…
- それぞれの囲った領域は重複してよい
- 各領域はできるだけ多くのセルを囲む
- 領域数はできるだけ少なくする
あたりがある。
これを踏まえ、全てを囲むと以下の図のようになる。
ここで、同じ色の領域は一つの囲いと捉えるようにしよう。
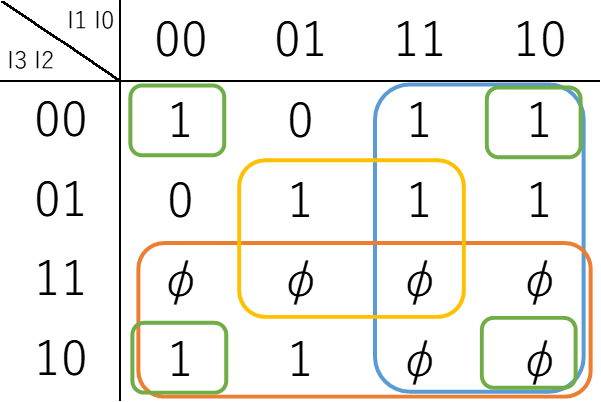
四隅の緑が見逃しがちなので、気を付けよう。
あとは、先ほどやったようにそれぞれの領域を表す項を求め、それらをORで取れば完成だ。
条件に従って丸を作っていると、その丸がかかっている入力で変化している部分、変化していない部分があるはず。
その変化していない部分が1ならその入力を、0ならそのNOTをANDで結んでいく。
そして、それぞれの丸の結果を、最後にORで取ればその出力のブール代数が完成する。
$$L_1 = \overline{I_2} \overline{I_0} + I_2 I_0 + I_3 + I_1$$
先頭から、緑、黄、オレンジ、青の領域に対応している。
ここまで簡単になった。
図で分かりやすいので、最も使いやすい簡略化の一つになるだろう。
正直、私もほとんどこれを使っている。
さて、視覚的、かつ直感的に使えて強力なカルノー図だが、弱点もある。
何かというと、入力が5以上になると図の書き方が難しくなるのだ。
一応、人の手で行うのは6変数くらいまでが限界だろう。
その場合、この表自体をさらに横や縦に並べ、その表同士も対応するセルが隣接していると捉えることで同じことが可能。
…だが、その場合は後で解説する3つ目の方法の方が早いかもしれない。
ブール代数による計算
さて、説明の順番を間違えた感が否めないが…二つ目に進んでいこう。
まあ、愚直に計算式をゴリゴリ変形していこう、というのがこの二つ目だ。
変形に使う法則は、第3回で紹介したものたちだ。
というわけで、\(L_2\)に対してやってみよう。
$$\begin{eqnarray}
L_2 & = & \overline{I_3} \overline{I_2} \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} \overline{I_2} \overline{I_1} I_0 \\
& + & \overline{I_3} \overline{I_2} I_1 \overline{I_0} \\
& + & \overline{I_3} \overline{I_2} I_1 I_0 \\
& + & \overline{I_3} I_2 \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & I_3 \overline{I_2} \overline{I_1} \overline{I_0} \\
& + & I_3 \overline{I_2} \overline{I_1} I_0 \\
& = & \overline{I_3} \overline{I_2} \overline{I_1} (\overline{I_0} + I_0) \\
& + & \overline{I_3} \overline{I_2} I_1 (\overline{I_0} + I_0) \\
& + & \overline{I_3} I_2 \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & I_3 \overline{I_2} \overline{I_1} (\overline{I_0} + I_0) \\
& = & \overline{I_3} \overline{I_2} \overline{I_1} \\
& + & \overline{I_3} \overline{I_2} I_1 \\
& + & \overline{I_3} I_2 \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & I_3 \overline{I_2} \overline{I_1} \\
& = & \overline{I_3} \overline{I_2} (\overline{I_1} + I_1) \\
& + & \overline{I_3} I_2 \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & \overline{I_2} \overline{I_1} (\overline{I_3} + I_3) \\
& = & \overline{I_3} \overline{I_2} \\
& + & \overline{I_3} I_2 \overline{I_1} \overline{I_0} \\
& + & \overline{I_3} I_2 I_1 I_0 \\
& + & \overline{I_2} \overline{I_1}
\end{eqnarray}$$
…一旦ここまでにさせてもらいたい。
これだけでもかなり大変なのがお分かりいただけると思う。
しかも、今この計算はドントケアも考慮していない状態のため、そこも考えるとより簡略化できることだろう。
まあ、方法は紹介したが…ぶっちゃけカルノー図を作る方が面倒な時(ドントケアがなく、入力数が3程度まで?)くらいしか使うタイミングはないだろう。
\(L_2\)に関しては、後で改めてカルノー図で簡略化することにしよう…
クワイン・マクラスキー法
さて、この方法なのだが…慣れないとなかなかに難しい。
そこで、論理式と並べながら、それぞれの手順が具体的に何をするものか、何を意味しているかを同時に説明していくことにしよう。
このクワイン・マクラスキー法は、表を活用しながら進めていく方法だ。
なお、ここからの手順はWikipediaを参照しながら進めていくので、よかったらこちらも見てみるといいだろう。
まず、この手法は大きく3つの段階からなる。
・関数の主項をすべて求める
クワイン・マクラスキー法 – Wikipedia
・求めた主項を表にまとめ、必須項を求める
・最簡形を求める
これだけ見ると何が何やら…という感じだと思うので、一個ずつ丁寧に見ていこう。
ここでは、\(I_4\)に対して実際に簡略化をしてみる。
関数の主項をすべて求める
いきなり分からない用語が出てきているが、先に手順を解説した後にどれが該当するかを解説しよう。
最初に、この出力\(L_4\)が1、もしくは\(\phi\)となる時の入力に関して、入力にいくつ1があるか、というのに注目する。
この入力内の1の個数について、0個から4個まで分類してまとめていく。
| 1の個数 | \(I_3 I_2 I_1 I_0\) | 名前 |
|---|---|---|
| 0 | 0000 | \(m_0\) |
| 1 | 0010 | \(m_2\) |
| 1 | 1000 | \(m_8\) |
| 2 | 0011 | \(m_3\) |
| 2 | 0101 | \(m_5\) |
| 2 | 0110 | \(m_6\) |
| 2 | 1001 | \(m_9\) |
| 2 | 1010 | \(m_{10}\) |
| 2 | 1100 | \(m_{12}\) |
| 3 | 1011 | \(m_{11}\) |
| 3 | 1101 | \(m_{13}\) |
| 3 | 1110 | \(m_{14}\) |
| 4 | 1111 | \(m_{15}\) |
名前の添え字は、その入力を2進数と捉え、10進数に変換したものをつけている。
この方法で名前を付けておくと、後で便利なので覚えておこう。
なお、この段階では1とドントケアを区別する必要はない。
では、ここから入力\(I_3 I_2 I_1 I_0\)について、1か所のみ異なる組み合わせを全て見つけていこう。
方針としては、行の先頭から順番に、次の個数のブロック全てを見比べて、1か所だけ異なればその組み合わせを作り出す。
例えば先頭の行、入力は0000だ。
1は一個も入っていないので、これと1の個数が一つの内容を比べる。
…まあ、当然全て該当し、今回は二つの組合せができる。
ここで、異なった1箇所をハイフンやアスタリスクなど別の記号で置き換え、新たな組み合わせとする。
新たな名前も付けるのだが、元となった組み合わせの添え字を全て付けてあげよう。
今注目している部分だと、\(m_{0, 2}\)は00*0、\(m_{0, 8}\)は*000となる。
次に、1の個数が1個の2行について、1の個数が2個のブロックと見比べる…というのを、全てで行う。
これで行った結果を以下の表にまとめよう。
| 1の個数 | \(I_3 I_2 I_1 I_0\) | 名前 |
|---|---|---|
| 0 | 00*0 | \(m_{0,2}\) |
| 0 | *000 | \(m_{0,8}\) |
| 1 | 001* | \(m_{2,3}\) |
| 1 | 0*10 | \(m_{2,6}\) |
| 1 | *010 | \(m_{2,10}\) |
| 1 | 100* | \(m_{8,9}\) |
| 1 | 10*0 | \(m_{8,10}\) |
| 1 | 1*00 | \(m_{8,12}\) |
| 2 | *011 | \(m_{3,11}\) |
| 2 | *101 | \(m_{5,13}\) |
| 2 | *110 | \(m_{6,14}\) |
| 2 | 10*1 | \(m_{9,11}\) |
| 2 | 1*01 | \(m_{9,13}\) |
| 2 | 101* | \(m_{10,11}\) |
| 2 | 1*10 | \(m_{10,14}\) |
| 2 | 110* | \(m_{12,13}\) |
| 2 | 11*0 | \(m_{12,14}\) |
| 3 | 1*11 | \(m_{11,15}\) |
| 3 | 11*1 | \(m_{13,15}\) |
| 3 | 111* | \(m_{14,15}\) |
この20個の組合せができた。
さて、先に進む前に…今、組み合わせることができなかった入力があるかを確認しておこう。
とはいっても、見比べてもらえれば分かるが、全ての入力を使ったので、まだ何もしなくていい。
では、今作った組み合わせで、もう一度同じことをする。
このとき、今回はアスタリスクを使って置き換えた部分も同じでなければいけない。
例えば、0*10と0*00は0**0にできるが、001*と0*00は00*0とか0***とかにできない、ということだ。
また、1か所のみ異なるというのも0と1の組み合わせのみなので、アスタリスクになった部分をもう一度置き換えないよう注意しよう。
先に言ってしまうと、これをそれ以上繰り返せないところまで繰り返す。
そして、最初は無かったが、そのうち使われない行も発生する。
その行には、何かしらの目印をつけておくようにしよう。
では、2段階目の組み合わせを作成してみる。
| 1の個数 | \(I_3 I_2 I_1 I_0\) | 名前 |
|---|---|---|
| 0 | *0*0 | \(m_{0,2,8,10}\) |
| 1 | *01* | \(m_{2,3,10,11}\) |
| 1 | **10 | \(m_{2,6,10,14}\) |
| 1 | 10** | \(m_{8,9,10,11}\) |
| 1 | 1*0* | \(m_{8,9,12,13}\) |
| 1 | 1**0 | \(m_{8,10,12,14}\) |
| 2 | 1**1 | \(m_{9,11,13,15}\) |
| 2 | 1*1* | \(m_{10,11,14,15}\) |
| 2 | 11** | \(m_{12,13,14,15}\) |
ここで、入力が全く同じになったものは名前も一致しているはずで、それらは一つにまとめている。
さて、先ほどの表と見比べてみると…\(m_{5,13}\)の*101が使われていない。
これは後で使うことになるので、覚えておこう。
で、これに対してもう一度行うと…\(m_{8,9,10,11,12,13,14,15}\)の1***だけが組み合わせで作ることができ、これも残ったものと同じ扱いになる。
というわけで、最終的に組み合わせを作れず、残ったものたちを以下に並べてみよう。
ここからは1の個数を気にしなくてもよくなるので、普通に並べてみる。
| \(I_3 I_2 I_1 I_0\) | 名前 |
|---|---|
| *101 | \(m_{5,13}\) |
| *0*0 | \(m_{0,2,8,10}\) |
| *01* | \(m_{2,3,10,11}\) |
| **10 | \(m_{2,6,10,14}\) |
| 1*** | \(m_{8,9,10,11,12,13,14,15}\) |
この表に載っているものたちが、主項と呼ばれるものだ。
さて、ここまでやっていたことを論理式の角度から見てみよう。
最初の状態で、\(m_0\)の0000と\(m_2\)の0010を組み合わせて、\(m_{0,2}\)、00*0を作り出した。
これは、両方ともこの入力の時に1を出力したい、という状況だったことを思い出そう。
つまり、論理式でいうと…
$$\begin{eqnarray}
m_0 + m_2 & = & \overline{I_3} \overline{I_2} \overline{I_1} \overline{I_0} + \overline{I_3} \overline{I_2} I_1 \overline{I_0} \\
& = & \overline{I_3} \overline{I_2} \overline{I_0} ( \overline{I_1} + I_1) \\
& = & \overline{I_3} \overline{I_2} \overline{I_0}
\end{eqnarray}$$
という操作をやっていることになる。
ようは、00*0のように*が入っている部分は、そこの入力に依らないことを表している。
そして、今全ての組み合わせで見ていた。
つまり、1になってほしい部分を簡単にする組み合わせを全て試したことになる。
主項というのは、そのままこれ以上簡略化できない項、と捉えてくれればいいだろうか。
なお、ドントケアも入れたのは、そこも1にすることができるからだ。
求めた主項を表にまとめ、必須項を求める
次に、この主項の中から必須項というものを求める。
ここでまた表を作るのだが…まず、横方向に出力が1となって欲しい入力の名前を、縦方向に先ほど求めた主項を並べる。
この横方向に、今度はドントケアとなっている出力を入れないのがポイントだ。
そして、セルには…これは、先に見てもらった方が早いだろう。
| \(m_0\) | \(m_2\) | \(m_3\) | \(m_5\) | \(m_6\) | \(m_8\) | \(m_9\) | |
|---|---|---|---|---|---|---|---|
| \(m_{5,13}\) | × | ||||||
| \(m_{0,2,8,10}\) | × | × | × | ||||
| \(m_{2,3,10,11}\) | × | × | |||||
| \(m_{2,6,10,14}\) | × | × | |||||
| \(m_{8,9,10,11,12,13,14,15}\) | × | × |
名前の付け方で分かりやすくなっているが…ようは、上に横へ並んでいるものは、組み合わせを作る元となったものたちだ。
そして、それを内包する形で左に縦へ並べた主項を求めた。
その、内包されている部分にチェックをつけていくことになる。
例えば、\(m_{0,2,8,10}\)には\(m_0, m_2, m_8, m_{10}\)の情報が詰まっているので、上に該当するものがあればそこに×印を入れていく。
ここで、必須項というものを求めるのだが、その方法は簡単。
各列(縦方向)を見て、×が1か所しかついていない主項が必須項だ。
…今回は全ての主項が該当するので、これらを全てORで取れば一番簡略化した形ということになる。
つまり…
$$L_4 = I_2 \overline{I_1} I_0 + \overline{I_2} \overline{I_0} + \overline{I_2} I_1 + I_1 \overline{I_0} + I_3$$
で\(L_4\)の簡略化が完了だ。
ちなみに、必須項の意味だが、例えば\(m_0\)で見てみよう。
主項の中からこの\(m_0\)を1にするためには、これを使ったものが必要だ。
今回は、\(m_{0,2,8,10}\)の一つだけ。
つまり、これを入れないと\(m_0\)の時に1とできないので、必須な主項となる。
だから、必須項だ、というイメージ。
最簡形を求める
さて、一応\(L_4\)の簡略化は終わってしまったが、ここからはWikipediaの例を借りて最後の手順を解説していこう。
とはいえ、上までの手順で必須項は求められるので、それ以外を考えるだけ。
Wikipediaの例で主項を求めた時点の表を以下に引用しよう。
| \(m_4\) | \(m_8\) | \(m_{10}\) | \(m_{11}\) | \(m_{12}\) | \(m_{15}\) | |
|---|---|---|---|---|---|---|
| \(m_{4,12}\) | × | × | ||||
| \(m_{8,9,10,11}\) | × | × | × | |||
| \(m_{8,10,12,14}\) | × | × | × | |||
| \(m_{10,11,14,15}\) | × | × | × |
なお、命名規則は上でやった\(L_4\)の時と全く同じだが、詳細はこちらで確認してほしい。
さて、今必須項は二つ。
これらは必ず使わなければいけないが、これだけだとまだ\(m_8\)だけカバーできていない。
そのため、必須項以外の主項から、どれを使うかを考えなければいけない。
…まあ、この例も見てもらえれば分かるが、残る二つのうちどちらを入れても\(m_8\)をカバーできるようになる。
また、この2つは両方とも構成する素子の数は変化しないので、いずれを選んでも回路の簡略化という視点では大丈夫だ。
今回は見ただけで分かったが、それでも分からない場合は、ペトリック法と呼ばれる方法で求めることができる。
が、ちょっと長くなりそうなので、今回その詳細は避けることにしよう。
他の出力
さて、手法の紹介が終わったところで、残る5つの出力もガンガン簡略化していこう。
クワイン・マクラスキー法はちょっと場所を取るので、カルノー図を用いる。
説明等は書かず、図と結果のブール代数のみ載せるので、やり方を忘れたら上に戻って確認してみよう。
\(L_2\)
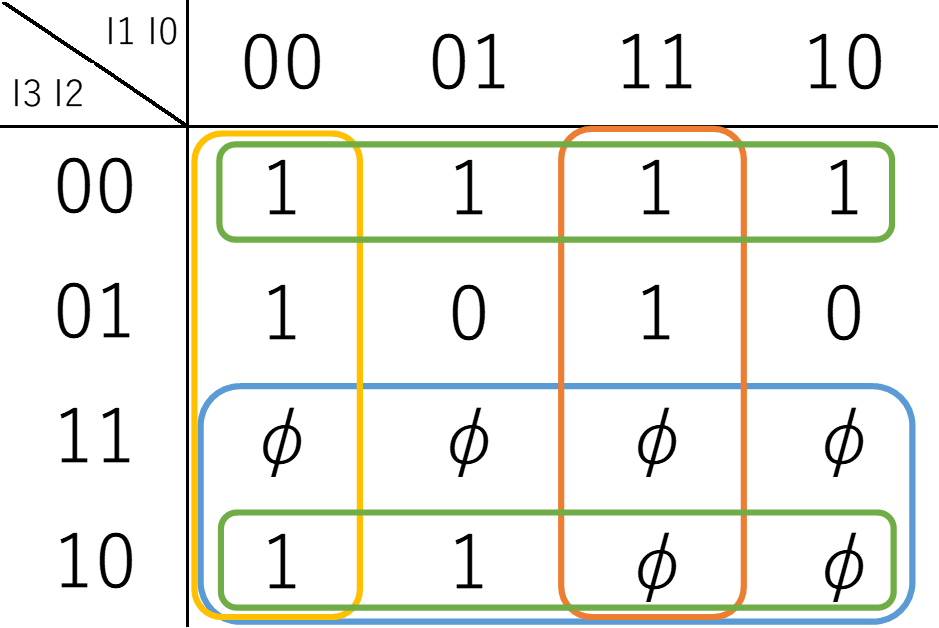
$$L_2 = I_3 + \overline{I_2} + I_1 I_0 + \overline{I_1} \overline{I_0}$$
\(L_3\)
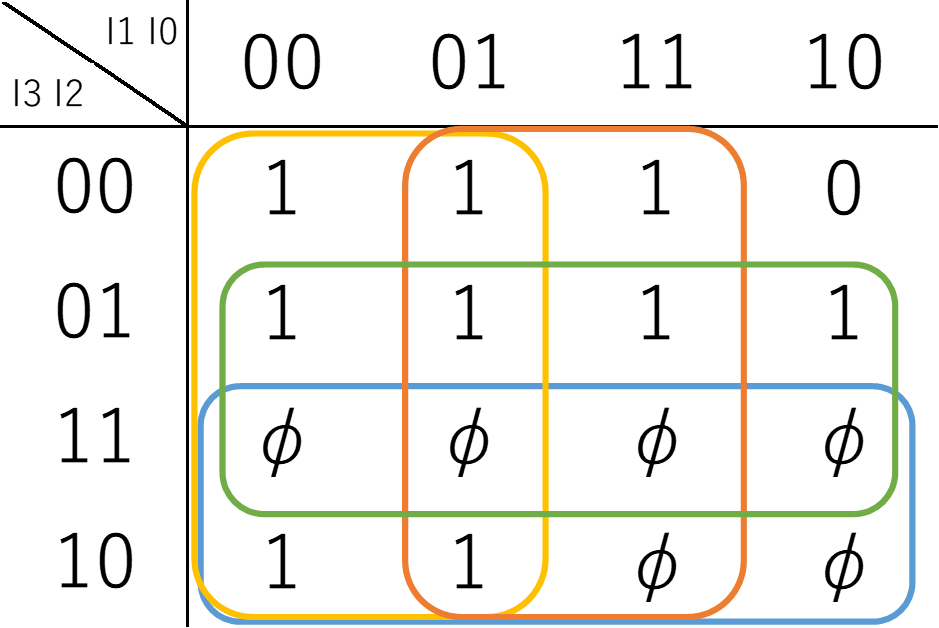
$$L_3 = I_3 + I_2 + \overline{I_1} + I_0$$
\(L_5\)
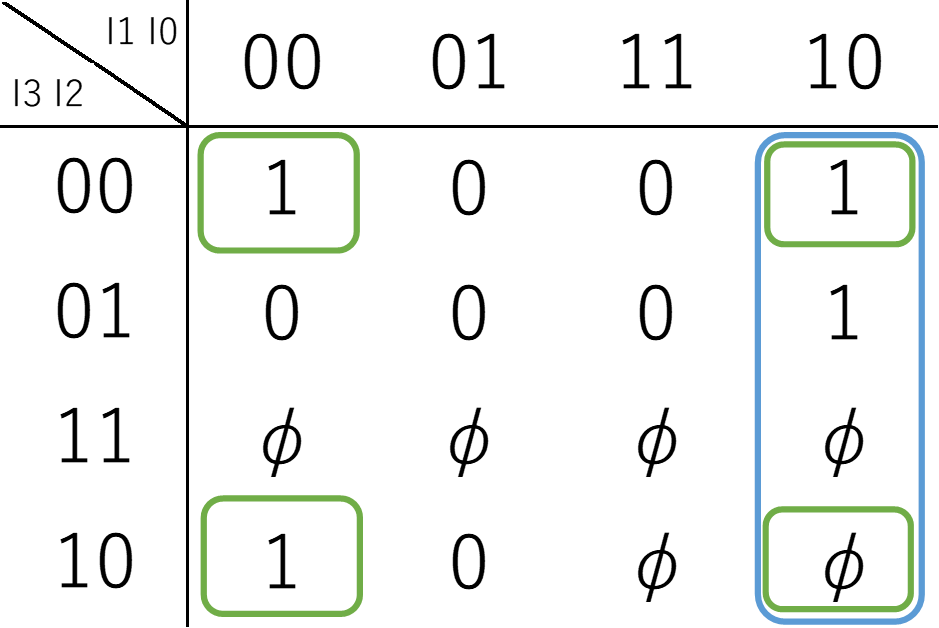
$$L_5 = \overline{I_2} \overline{I_0} + I_1 \overline{I_0}$$
\(L_6\)
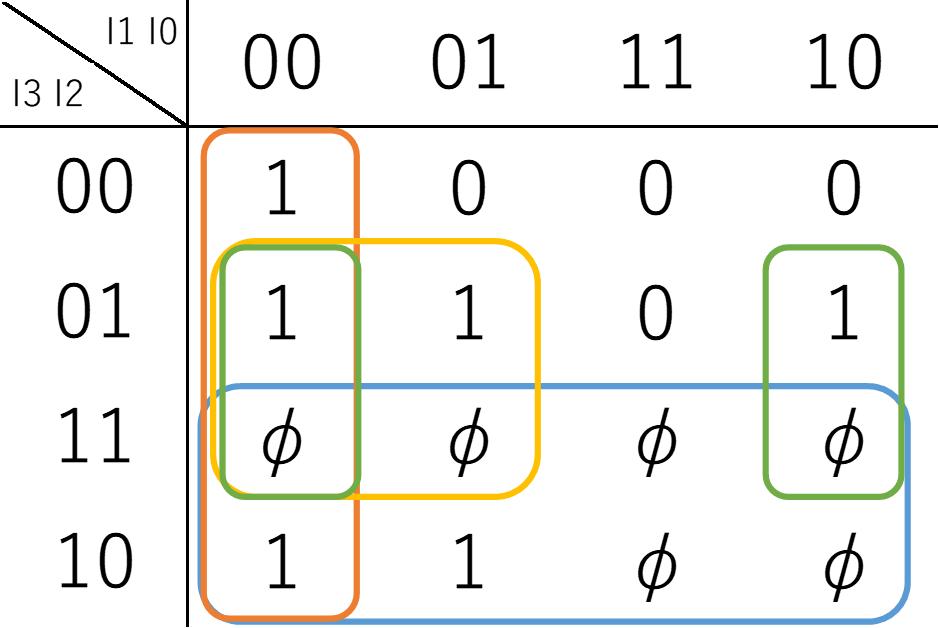
$$L_6 = I_3 + I_2 \overline{I_1} + I_2 \overline{I_0} + \overline{I_1} \overline{I_0}$$
\(L_7\)
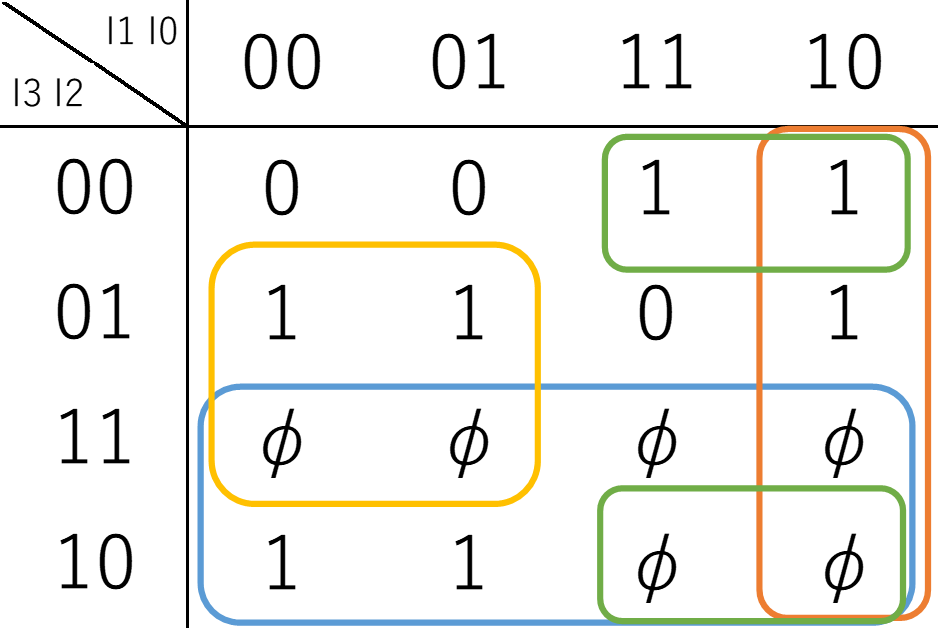
$$L_7 = I_3 + \overline{I_2} I_1 + I_1 \overline{I_0} + I_2 \overline{I_1}$$
7セグメントの論理回路図
では、ようやく論理回路図を作ろう。
とはいえ、論理式は全て出揃っているので、あとは素直に繋いでいくだけだ。
以下に、その論理回路図を載せる。

だ、だいぶ大きくなってしまった…
が、これで動かして問題ないことも確認できたので、これで完成だ。
おわりに
今回は、7セグメントに10進数を出力することを想定して、回路を簡略化する手法を実際に使いながら解説した。
一応ブール代数をゴリゴリ変形する方法もあるが…メインはカルノー図とクワイン・マクラスキー法のどちらかになるだろう。
余談だが、この二つは見た目は違えど、やっていることはほぼ全く同じだ。
カルノー図は視覚的に分かりやすい等、クワイン・マクラスキー法はアルゴリズムとして手順が明確なのでプログラムしやすい等というメリットがある。
状況によって、どちらがいいか考えて使い分けるようにしよう。
もし余力があれば、今度は7セグメントを2つに拡張し、0から15までを表示する回路、あるいは入力を符号付きで考え、マイナスの表示も行う回路あたりを作ってみると練習になると思う。
このどちらもドントケアは出てこないが、それも練習したい場合は…適当に真理値表を作って、それを実装してみるのもいいかもしれない。
何も、現実的に使えるものしか作ってはいけないということは一切ないので、色々試して遊んでみよう。
ちなみにだが、いずれの手法を使うとしても、当然ながら最初は真理値表を作るところから始まる。
その真理値表で間違ってしまうと、その後どれだけ正確に計算しても結果がズレてしまうので、細心の注意を払おう。
実は、私もこの記事に載せた回路を作る時に最初の真理値表を1か所間違えており、作り直している。
かなり手間が増えてしまうので、しっかり確認してから次に進むようにしよう。
…で、これを作った後に気づいたことがある。
電卓では、大体10桁近くの10進数を表示することになる。
それをどう組めばいいか、という問題だ。
9桁としても、2進数では符号付き31桁…つまり、31入力というとんでもない回路になってしまう。
恐らく、そこはもっと上手いやり方があると思うので、勉強を進めつつどうするか模索してみることにしよう。
さて、次回の話を。
次回から、ようやくではあるが順序回路に入ろうと思う。
前にもちらっと出したが、出力を再度入力に使いまわすことによって、情報を保持できるようにしたものだ。
その中でも、最も基本にあたるフリップフロップを次回解説する。
4種類ほどあるので、それぞれの違いにも気を付けながら進めていこう。




コメント