前回は意味理解のうち、
単語の意味を推測するための考え方を一つご紹介した。
概念体系や、シソーラスといったものを使う手法だ。
ただ、これには問題点があった。
それを克服するための方法の一つとして、
すでに書かれた、あるいは話された文章である
コーパスを用いる手法を、今回はご紹介しよう。
数式も出てくるが、必要な知識は
オマケとして入れてあるのでご安心を。
なお、本講座は以下の本を参考に進めている。
もしよかったら、中身を覗いてみて欲しい。
分布意味論
分布意味論とは
さて、いきなり用語だ。
分布意味論とは、考え方の一種。
ある単語がどんな文脈中に出やすいかという
統計的傾向が、その単語の意味的特徴を表している
という考え方になる。
分かりやすくするために、例を出そう。
例えば、「パソコン」という単語。
これが出てくるとき、前後には以下のような
単語が比較的出てくる可能性がある。
- インターネット
- ファイル
- 起動
- 操作
- 速いor遅い
また、もう一つ「スマホ」でも見てみよう。
- インターネット
- アプリ
- 起動
- 操作
- 軽い
こんな感じだろうか。
で、この二つは、意味が分かっている
我々からすると似ていると分かるだろう。
これを機械で処理する場合は、
上に出てきた単語に重複があるかを見る。
今回、「インターネット」、「起動」、
「操作」が共通している。
だから、この二つの単語は似ているっぽいぞ、
という判定が行える、ということだ。
分布仮説
そもそも、分布意味論というのは、
「同じ文脈に出現する単語は、同じような意味を持つ」
という仮説の基に成り立っている。
この仮説のことを、分布仮説と呼ぶ。
分布意味論による単語の意味表現は、
コーパスからその単語の共起語を求めることで
得ることができる。
共起語とは、文章中である単語と一緒に
出現する単語のことだ。
これは、次のチャプターで詳しく解説する。
とにかく、この考え方を用いれば、
様々な種類のコーパスを読み込むことで、
新しい言葉などにも応用することができるのだ。
共起語と自己相互情報量
共起語
上でちらっと書いた通り、共起語とは
文章中でよくセットで使われる単語のこと。
この定義は様々あり、
「文章中で一緒に出現する」という条件は、
以下のようなものが考えられる。
- 同一文章中に出現する
- 同一文中に出現する
- 前後\(n\)単語以内に出現する
- 係り受け関係にある文節内に出現する
自己相互情報量
自己相互情報量とは、単語間の関係…
共起の度合いを表す際に用いられる数式だ。
そもそも、この共起の度合いを
どのように考えるかだが、
単純にセットで出てきた回数を見る、
というのが自然だろう。
しかし、実際には頻繁に出てくるか、
あるいはほぼ出てこないかといった状態に
強く影響されてしまう。
そこで、その出現頻度の影響を無くす考え方が、
この自己相互情報量なのだ。
省略して、PMIと呼んだりもする。
では、数式を定義していこう。
コーパスにおける単語\(w\)の出現頻度を\(P(w)\)とする。
また、二つの単語\(w_1, w_2\)の
共起確率を\(P(w_1, w_2)\)と置く。
すると、このPMIは以下の式で定義される。
$$PMI(w_1, w_2) = \log \frac{P(w_1, w_2)}{P(w_1) \times P(w_2)}$$
…ただ、これだとちょっと計算がしづらい。
そもそも、共起確率って何だよという感じだと思う。
なので、新しく、
単語の出現回数を\(\mbox{count}(w)\)、
二つの単語の共起回数を\(\mbox{count}(w_1, w_2)\)、
コーパスの総単語数を\(T\)として、
以下の式で定義しなおす。
$$PMI(w_1, w_2) = \log \frac{T \times \mbox{count}(w_1, w_2)}{\mbox{count}(w_1) \times \mbox{count}(w_2)}$$
これなら、個数をカウントすれば求められる。
この二つの単語に意味的関連がなく、
互いに独立と見なせる場合は、
PMIは理論的には0となる。
また、正の相関がある場合は値も正になるのだ。
なお、この正の場合のみに着目して、
その他(マイナスの場合)はゼロとして考えることもある。
その他、単語自体の出現回数が少ない場合は、
値が異常に大きくなるときがある。
これを考慮し、
一定の出現回数以下の場合は除外する、
といったこともある。
単語共起行列と共起語ベクトル
\(N\)単語のコーパスについて、
その任意の組み合わせに対しての共起の度合いを求めて、
\(N \times N\)の行列を作ることができる。
共起の度合いは、共起回数や上で解説したPMIを用いる。
この行列のことを、単語共起行列と呼ぶ。
例としては、以下のような感じだ。
| 犬 | 学校 | … | パソコン | |
|---|---|---|---|---|
| 犬 | 0 | 4 | … | 1 |
| 学校 | 4 | 0 | … | 7 |
| … | … | … | … | … |
| パソコン | 1 | 7 | … | 0 |
この横一行は、ある単語がどのような
共起語を持つかを、その共起の度合いとともに
ベクトルとして表現したものとなっている。
このベクトルのことを、共起語ベクトルという。
また、この中で共起の度合いが
一定以上の共起語を、頻出共起語と呼ぼう。
分布類似度
さて、ここでまた類似度だ。
ここまでで、各単語には
コーパスから求めた共起語ベクトルが得られている。
あとは、このベクトルがどの程度似ているか
を調べられればいい。
これに使えるのが、コサイン類似度というもの。
とはいえ、考え方は簡単。
この二つのベクトルのなす角の
コサインを求めればいいだけだ。
…さて、数学よりの話になってきた。
なぜコサインを求めるかは、
今回のオマケとして載せよう。
一旦、このまま議論を進める。
で、二つの単語の類似度を求めるには、
以下の式で計算すればいい。
$$
\begin{eqnarray}
\mbox{similarity}(w_1, w_2) & = & \cos \theta \\
& = & \frac{v_{w_1} \cdot v_{w_2}}{|v_{w_1}| \times |v_{w_2}|}
\end{eqnarray}
$$
…この数式の具体的な計算方法も、
オマケに入れておこう。
コサインの定義から、この類似度は
常に\(-1\)以上、\(1\)以下の範囲を取る。
ただし、個数のベクトルの場合など、
マイナスの値を要素に持たない場合は0以上だ。
なお、類似度に関してはもう一つ考え方がある。
それが、頻出共起語集合というものを用いる手法。
この集合は、共起の度合いが
一定以上のものを集めたものだ。
この頻出共起集合を二つの単語で求め、
どの程度重なっているかを類似度とみなす。
これにはいくつか数式があり、
3つほど例を以下に示そう。
| 名前 | 数式 |
|---|---|
| Jaccard係数 | $$\frac{|X \cap Y|}{|X \cup Y|}$$ |
| Simpson係数 | $$\frac{|X \cap Y|}{\min(|X|, |Y|)}$$ |
| Dice係数 | $$\frac{2 \times |X \cap Y|}{|X| + |Y|}$$ |
問題点
さて、この方法にも問題点がある。
単語の種類だけ要素が存在する
ベクトルを扱うので、次元数が大きいのだ。
実際に共起している単語は少数なので、
多くの要素がゼロとなっている。
これについては、
次元を削減するための手法も研究されている。
が、もう一つ、アプローチがある。
…実は、機械学習のところで飛ばした
ニューラルネットワークを用いる手法だ。
というわけで、
このニューラルネットワークの説明も必要になった。
おわりに
今回は、単語の意味理解の二つ目を解説した。
この後オマケで数学的な知識の補足を行うので、
よかったらそこまで見てみて欲しい。
次回は、一旦ニューラルネットワークの説明を行おう。
もし短くなるようであれば、
単語の意味理解にどう使うかまで触れようと思う。
オマケ:コサイン類似度
ここからは数学のお話だ。
本文中で出た、なぜベクトルの類似度が
コサインで求められるかというお話
…の前に、三角関数からお話しよう。
三角関数とは
以下のような直角三角形を考える。
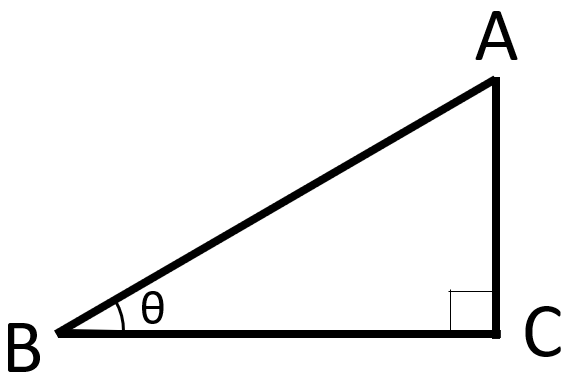
このとき、三角関数というものを考えることができる。
三角関数とは、ある角度\(\theta\)によって決まる数値で、
以下のように求められる。
$$\sin \theta = \frac{AC}{AB}$$
$$\cos \theta = \frac{BC}{AB}$$
$$\tan \theta = \frac{AC}{BC}$$
角度\(\theta\)によって、
この数値が変わるのは大丈夫だと思う。
ここからは、コサインのみに注目しよう。
BCの長さを固定した状態で
角度が小さくなる、つまりABとBCが近づくと、
コサインの値は1に近づくのは分かるだろうか。
ABの長さが、BCに近づくからだ。
逆に、角度が大きくなると、
ABの長さはどんどん長くなっていく。
式を見ると、ABは分母に入っているので、
コサインの値は0に近づいていくのだ。
つまり、
角度が小さくなると…つまり、
二つの線が同じ方向を向くと
コサインの値が大きくなっていく。
まずは、ここまでを抑えておいて欲しい。
ベクトル
さて、こちらも解説せねばならない。
ベクトルは、以前複数の値をセットにしたもの、
というような解説をしたと思う。
それもまあそうなのだが、
もう一つの説明のしかたがある。
それは、大きさと向きを持つ、ということだ。
例えば、二つの二次元ベクトル
(1, 2)、(2, 1)を見てみよう。
図にすると以下のようになっている。
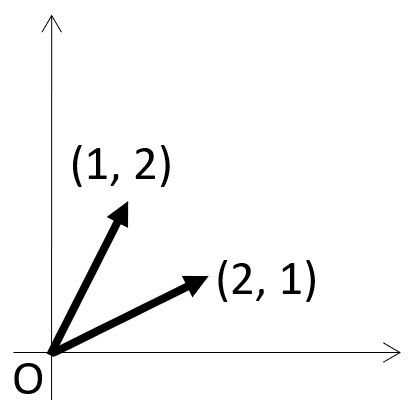
さて、上で二つのベクトルの類似度として
コサインを求めると説明した。
このベクトルが似ているというのが、
似た方向を向いている、という考え方なのだ。
つまり、その間の角度を\(\theta\)として、
そのコサインを求めればいい、ということになる。
コサインは、同じ方向を向いていれば大きくなるからだ。
では、これをどうやって求めるか、
というのが次なる課題だ。
このために、ベクトルの内積という定義を使う。
二つのベクトル\(v_1, v_2\)の内積は、
その二つがなす角を\(\theta\)として
以下の式で表される。
$$v_1 \cdot v_2 = |v_1| \times |v_2| \times \cos \theta$$
これは定義なので、
なんでこの式になるかは気にしないでおこう。
この両辺をコサインの係数で割れば…
$$\cos \theta = \frac{v_1 \cdot v_2}{|v_1| \times |v_2|}$$
と、類似度の式そのままが出てくる。
あとは、それぞれの計算式が分かれば大丈夫だ。
まず、内積\(v_1 \cdot v_2\)について。
これは、各ベクトルそれぞれの一個目、二個目、…
を掛けて、それらを全て足せばいい。
次に、バーティカルバーで囲まれた\(|v_1|\)←こいつ。
これは、そのベクトルの大きさで、
各要素を全て二乗し、それらを全て足し合わせた後に
平方根を求める。
これらを使って、実際に
コサイン類似度を一個計算してみよう。
さっき出した、(1, 2)、(2, 1)で見てみよう。
まず、内積は
$$1 \times 2 + 2 \times 1 = 2 + 2 = 4$$
となる。
次に、大きさ…これは両方一緒なので、
片方だけ出そう。
$$\sqrt{1^2 + 2^2} = \sqrt{5}$$
では、最後にコサイン類似度を求める。
$$\cos \theta = \frac{4}{\sqrt{5} \times \sqrt{5}} = \frac{4}{5}$$
よって、類似度が0.8と分かった。
これは、次元数が大きくなっても同じ方法で求められる。
今回は、あくまで計算方法が分かるまでを解説したので、
より詳しい解説は是非調べてみて欲しい。



コメント