今回解説する分の問題を解いてて、気づいたことがある。
なんと、表現の違いを無視すれば、数字まで全く同じの計算問題が出ることがあるのだ。
実際、今回の解説範囲の中で、いくつかすでに解説したことのある問題が出てきている。
そこについては、解説済みの部分へリンクを貼ることとしよう。
数字くらいは変わっているだろう、と踏んでいたので、予想外だ。
というわけで、今回も応用情報過去問の計算問題解説記事だ。
今回の解説対象は、「平成30年度 春季 応用情報技術者試験 午前」になる。
いつも通り問題文は上のリンク先参照、計算問題は独断と偏見で選んでいる。
また、備忘録なので誤り等含まれてたら申し訳ない。
その場合は教えていただけると幸いだ。
では、内容に入っていこう。
問2
まずは、ビット変換に関する計算問題だ。
問題に、文字とそれをビット表記にしたもの、出現確率が提示されている。
このとき、1文字あたりの平均ビット数はいくつになるか、というものだ。
これについては、各文字についてビット表記の桁数を数え、それに出現確率を掛けたものを足し合わせればいい。
ちょっと、表にビットの桁数と掛け算の結果を書き加えてみよう。
| 文字 | ビット表記 | ビット桁数 | 出現確率(%) | 掛け算の結果 |
|---|---|---|---|---|
| A | 0 | 1 | 50 | 0.5 |
| B | 10 | 2 | 30 | 0.6 |
| C | 110 | 3 | 10 | 0.3 |
| D | 1110 | 4 | 5 | 0.2 |
| E | 1111 | 4 | 5 | 0.2 |
あとは一番右の列を全部足せばいいだけなので、計算すると答えは1.8、イが正解になる。
問3
ハミング符号の問題。
方針としては、まずどのビットが誤りかを求める。
それが分かれば、そのビットを反転させることで答えが得られる。
では、まず誤っているビットを探していこう。
元々、以下の条件式が成り立つように\(P_1, P_2, P_3\)が設定されていた。
- \(X_1 \oplus X_3 \oplus X_4 \oplus P_1 = 0\)
- \(X_1 \oplus X_2 \oplus X_4 \oplus P_2 = 0\)
- \(X_1 \oplus X_2 \oplus X_3 \oplus P_3 = 0\)
そして、今得られているハミング符号は1110011となっているため、各変数には以下のように値が入っていることが分かる。
問題文に書かれている通り、順番通りに綺麗に並んでいるわけではないのに注意しよう。
| 変数 | 値 |
|---|---|
| \(X_1\) | 1 |
| \(X_2\) | 1 |
| \(X_3\) | 1 |
| \(X_4\) | 0 |
| \(P_1\) | 1 |
| \(P_2\) | 1 |
| \(P_3\) | 0 |
さて、では条件式の計算をそのまましてみよう。
- \(1 \oplus 1 \oplus 0 \oplus 1 = 1\)
- \(1 \oplus 1 \oplus 0 \oplus 1 = 1\)
- \(1 \oplus 1 \oplus 1 \oplus 0 = 1\)
元々の条件式は全て0だったのに対し、今回は全てが1になっている。
また、問題文から、今回誤りは1ビットのみ存在している。
この二つの情報から、全部の条件式に含まれる\(X_1\)が誤っているビットだと特定できる。
あとは、そのビットを入れ替えてあげればいいので、0110011が訂正後のハミング符号となり、アが正解だ。
問4
ただの計算問題。
まず、サンプリング周波数が40kHzと書かれているので、1秒間に40k回のサンプリングを行っている。
その1回あたり、16ビットの情報量を持つ。
求める単位がバイトなので、先に2バイトに直しておこう。
あとは、単純に掛け算すればいいので、
$$40k \times 2 = 80k$$
聞かれているのは何kバイトかなので、80のウが正解になる。
問5
ちょっと面倒な、再帰関数の問題。
大人しく、\(Ack(1, 3)\)を計算していこう。
$$Ack(1, 3) = Ack(0, Ack(1, 2))$$
\(Ack(1, 3)\)を求めるためには、\(Ack(1, 2)\)を求めなければいけない。
$$Ack(1, 2) = Ack(0, Ack(1, 1))$$
今度は\(Ack(1, 1)\)が必要だ。
$$Ack(1, 1) = Ack(0, Ack(1, 0))$$
そして、\(Ack(1, 0)\)。
$$Ack(1, 0) = Ack(0, 1)$$
定義を見ると、\(Ack(0, 1) = 2\)と分かるので、順番に戻していく。
$$Ack(1, 1) = Ack(0, 2) = 3$$
$$Ack(1, 2) = Ack(0, 3) = 4$$
$$Ack(1, 3) = Ack(0, 4) = 5$$
ということで、答えはウの5となった。
落ち着いて、どんな値が欲しくて、それを求めるためにはどうすればいいかを追っていこう。
問6
探索における比較回数の計算問題だ。
昇順に並んでいる\(n\)個のデータを\(m\)個ごとに分割し、以下の手順でデータを探していく。
- まず、各ブロックのどこに該当データが入っているかを探すため、線形探索で各ブロックの末尾と比較する。
- 次に、1で見つけたブロック内のデータを線形探索で比較して目的のデータを見つける。
この、平均の比較回数を出してあげればいい。
前提として、両方とも線形探索、先頭から順番に数えていく方式なので、比較回数の平均は最大値を2で割ったもの…つまり、探索するデータ数の半分として考えられる。
まず、手順1について見ていこう。
これを求めるためにはブロック数が必要になるが、単純に\(\frac{n}{m}\)で求められる。
今聞かれているのは平均の比較回数なので、2で割って\(\frac{n}{2m}\)回となる。
次に、手順2について。
今度は\(m\)個のデータについて同じように考えればいいので、\(\frac{m}{2}\)回。
これを足し合わせた\(\frac{m}{2} + \frac{n}{2m}\)、イが正解になる。
問16
定番の稼働率の問題。
…なのだが、これまで解説してきたものよりちょっとだけ考えなければいけないことが増えている。
まず、システムの構成を見ていこう。
今、負荷分散装置、APサーバ、DBサーバ、磁気ディスク装置と並んでいる。
負荷分散装置と磁気ディスク装置は壊れないそうなので、ここからは一旦無視して進めよう。
問題文を見ると、AP、DBはそれぞれ最低でも1台動いていればいい、とある。
逆に、APの2台ともとか、DBの2台ともが動いていないとアウトだ。
つまり、APの2台で並列、DBの2台で並列になっており、それらが直列に繋がっていると考えられる。
図に直すと以下の通りだ。
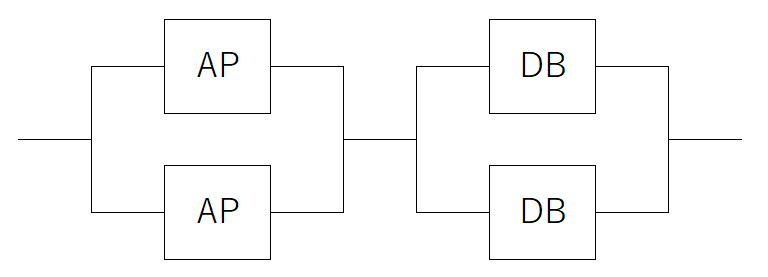
ここまで分かれば、あとは単純な稼働率の問題になる。
復習として、直列の場合は二つの稼働率の掛け算、並列の場合は1から両方とも稼働していない率を引けばいい。
まず、AP、DBそれぞれで見ていこう。
今、計算対象となるサーバの稼働率はどれも0.8なので、AP全体、DB全体それぞれで見た場合の稼働率は以下のようになる。
$$1 – (1 – 0.8)^2 = 0.96$$
あとは、稼働率0.96のサーバが直列で繋がっているとみなせるので…
$$0.96^2 = 0.9216 \sim 0.92$$
よって、ウが正解だ。
問17
タスクに関する計算問題。
だが、多少知識も絡んでくる。
まず、3つのタスクについて、どの時間で何の処理をしているかを図にしてみよう。
前提として、CPU処理はどれか1タスクずつしかできないのに対し、IOは競合しないので重複して実行できる。
また、求める実行可能状態の時間は、他の処理のせいでCPU空き待ちになっている時間を指している。
というわけで、タスクCについて、求めたい時間を黄色で塗りつぶしたものが以下だ。

最初、0秒で全てが実行可能状態になる。
一番優先度の高いAがまず実行状態に移り、その間BとCは実行可能状態のままだ。
AのCPU処理が終わると、IO処理に移り、CPUが空くので、次に優先度の高いBが実行される。
同じように、BがIO処理に入ったら、CのCPU処理開始だ。
まずここで、4秒間の実行可能状態がある。
次に、IOが全てのタスクで同時に終わり、また同じようにAから処理が開始される。
このとき、Cは6秒間待たされているので、合計して10秒、ウが答えだ。
問21
大定番、論理回路の問題だ。
一度に全部考えるのはつらいので、段階的に考えていこう。
まず、左のA NAND Bを①とする。
次に、真ん中の縦に並んでいるNANDの上を②、下を③。
最後に、Yの直前のNANDを④としよう。
これで、AとBの値から各出力がどうなるかの真理値表を書く。
| A | B | ① | ② | ③ | ④=Y |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
ということで、入力A、Bと出力Yだけに注目すると、これは排他的論理和になっている。
これを表したものはウなので、これが正解になる。
ちょっと回路が複雑なので、段階的に答えを出すようにしよう。
なお、回路図のどれが何かわからない、という場合は…実は問題冊子の問1の前に対応表が載っている。
覚えるに越したことはないが、最悪ここで確認してもいいだろう。
問22
ぱっと見は難しそうだが、意味さえ分かってしまえば楽な問題だ。
先に、図の見方を確認していこう。
問題文を読むと、クロックの立ち上がりエッジでデータを最下位ビットに取り込むと書かれている。
その前にあったデータは1ビットずつ上位へシフトだ。
図を見ると、クロックの波の左から点線が伸びている。
そこが、データの取り込みタイミングだ。
そして、ストロープの立ち上がりエッジで、今確保しているデータのうち、下から8ビット分を確定とする。
つまり、これが実行された時点でシフトレジスタの値が更新される。
図で見てみると、ストロープにも一つだけ波があり、その左からまた点線が出ている。
このタイミングで確保されていたデータの下から8ビットが、最終的に答えになる。
ということで、ストロープまでにデータ取り込みで得られるビットを並べてみよう。
データは上が1、下が0なので、110001101となる。
最後のクロックはストロープ後のため関係ないので注意。
そして、ストロープで下8ビットを結果として確定するので、10001101が確定後のシフトレジスタの値だ。
聞かれているのが16進数での値なので、これを直して8D、イが正解だ。
問23
これもぱっと見難しそうだけど、実は簡単なタイプだろう。
まず、発振器から15MHzのクロックが出ている。
ここからPLL1、分周器を通して、115kHz(±5%)にしたい。
さて、PLL1には8逓倍(読み:ていばい)と書かれている。
これは、周波数を8倍にするという意味なので、求めたい分周器には15M×8=120MHzの周波数が供給されている。
これを115kHzにするので、あとは割り算だ。
$$\frac{115k}{120M} \sim 0.96 \times 10^{-3}$$
5%の誤差が許されているので、大体で構わない。
ということで、大雑把に1000分の1くらいにすればいいことが分かる。
これに最も近いのは\(2^{10} = 1024\)、エが正解となる。
問31
これも定番、通信速度の問題だ。
まずは通信速度と送る容量を求め、そこから秒数を算出していく。
先に通信速度から見ていこう。
元々100Mビット/秒で、伝送効率が50%なので、実際の速度は50Mビット/秒となる。
次に送る容量。
1000バイトの電文を1000件、先にビットに直して8000ビットが1000件だ。
ということで、単純に掛け算して、ついでに単位を直して8Mビットとなる。
あとは、送る容量を速度で割ればいいので、
$$\frac{8M}{50M} = 0.16$$
よって、答えはウだ。
問33
今度はビット誤り率の問題。
今回、100秒に1回の1ビット誤りがあるとのことなので、100秒間に送れるデータで1を割ってあげればいい。
1秒では30Mビット送れるとのことなので、100秒間は単純に100倍だ。
ということで計算すると…
$$\frac{1}{30 \times 10^6 \times 100} \sim 3.33 \times 10^{-10}$$
より、答えはイだ。
問35
ネットワークアドレスの問題。
サブネットマスクが上位23桁なので、第3オクテットだけ見ていこう。
まず、それぞれのIPアドレスを2進数に直す。
- 192.168.0.0/23 → 0000 0000
- 192.168.2.0/23 → 0000 0010
下線を引いたところまでがネットワークアドレスとなる。
さて、この二つを集約したいので、一つサブネットマスクの範囲を縮めよう。
そして、そこまでを全て0にすれば、両ネットワークが一つのネットワークアドレスに属することになる。
よって、第3オクテットは、まず2進数で0000 0000となる。
これを元に戻して、192.168.0.0/22が集約後のネットワークアドレス、つまり答えはアだ。
問54
工数の問題だが、よくよく見るとただの計算問題。
開発工数\(E\)(人月)と、開発規模\(L\)(キロ行)の関係について、\(E = 5.2L^{0.98}\)と与えられている。
\(L = 10\)のときの生産性を求めろ、というものだ。
生産性の求め方は、実は単位から推測できる。
生産性の単位はキロ行/人月なので、開発規模を開発工数で割ればいいとわかるのだ。
あとは計算。
$$\frac{L}{E} = \frac{10}{5.2 \times 10^{0.98}}$$
と、ここでワンポイント。
今回聞かれているのがおよそなので、\(10^{0.98}\)は大体10として計算できる。
ということで、続きを計算していくと…
$$\frac{10}{5.2 \times 10} = \frac{10}{52} \sim 0.2$$
よって、大体0.2となったので、答えはアだ。
0.98乗とかだとなかなか計算がしづらいので、およその場合は丸めてしまおう。
問63
これは、ちょっと表現は違うものの、本質は令和元年度秋の問64と全く同じ問題だ。
その時の解説を上のリンクに貼ったので、そちらを参照してほしい。
問72
部品計算の問題。
まず、製品Aを1個作るのに必要な部品Cの個数を求めていこう。
製品Aを1個作るためには、部品Bが2個、部品Cが1個必要だ。
そして、部品Bを作るために、部品C~Eが1個ずつ必要になる。
よって、製品Aを1個作るためには、部品Cは1 + 2 = 3個必要と分かる。
今、製品Aを10個作りたい。
そして、部品Bの在庫数はゼロ、部品Cは5個あるようだ。
まず、製品Aを10個作るためには、部品Cは合計で3 × 10 = 30個必要になる。
そして、元々5個はあるので、30 – 5 = 25個発注する必要がある。
よってウが正解だ。
問74
グラフの読み取り問題、知識がなくても案外なんとかなるタイプだ。
まず、グラフの曲線を見ると、不良率が大きくなれば必ず合格する確率が下がることが分かる。
それを踏まえて、各選択肢を見ていこう。
まずア、不良率がp1%よりも大きいと、合格率はL1より小さくなるので不適。
次にイ、(1.0 – L1)とは不合格となる確率で、グラフで言うと合格率1.0の右にラインが引かれているとして、それと曲線の間の距離になる。
今、不良率がp1%より左の部分を見ると、明らかに狭くなっていることが分かるので、これも不適。
そしてウ、合格率p2%より右を見ると、曲線はL2未満になっているので、ウが正解だ。
一応エも見ると、不良率p2%よりも左について、不合格となる確率に注目しているので曲線の上の部分だ。
これは、(1 – L2)よりも小さくなっているので、これも不適だ。
問75
これもすでに解説したことのある問題。
令和元年度秋の問74と全く同じだ。
これもリンクを貼っておいたので、そちらを参照してほしい。
問76
PC処分時の除去損の計算だ。
まずは、処分時のPCの評価額を計算していこう。
耐用年数が4年、2年間使用した後に処分をすると書かれている。
また、減価償却方法は定額法で、その償却率は0.250ということなので、1年で25%ずつ価値が下がっていくと考えることができる。
よって、処分時のPCの評価額は、
$$30 – (30 \times 0.25 \times 2) = 15$$
より、15万円とわかる。
あとは、廃棄費用2万円を足せばいいので、15 + 2 = 17より17万円、エが正解になる。
問77
損益分岐点分析の問題、これも定番だ。
今回は、単純に損益分岐点売上を求めればいい。
そのために必要な式をおさらいしておこう。
まず、先に変動費率を求めなければいけない。
$$変動費率 = \frac{変動費}{売上}$$
これを使って、損益分岐点売上を以下の式で求めることができる。
$$損益分岐点売上 = 固定費 \times \frac{1}{1 – 変動費率}$$
まず、変動費や固定費がバラバラになっているので、それぞれ合計して表を書き直してみよう。
| 項目 | 金額(単位:百万円) |
|---|---|
| 売上高 | 500 |
| 変動費 | 300 |
| 固定費 | 180 |
| 利益 | 20 |
あとはひたすら計算だ。
まず、変動費率を求めると…
$$\frac{300}{500} = 0.6$$
となる。
次に、損益分岐点売上を出していこう。
$$180 \times \frac{1}{1 – 0.6} = 450$$
ということで、450百万円となり、答えはウだ。


コメント