本シリーズでは、以下の本に沿って解説を書いている。

前回は、またしても新しい有限オートマトンである\(\varepsilon\)入力付き非決定性有限オートマトンを解説した。
状態遷移でこれまでに使っていなかった様相やステップといった概念を導入したが、言っていることはわりと単純だ。
今回の内容の元でもあるので、不安なら復習しておこう。
以下がその記事だ。
さて、今回は定理と証明の回。
この\(\varepsilon\)nfaと、以前解説したnfaで、認識できる言語に差がないことを示す。
nfaの解説は以下をご覧いただきたい。
これが言えると、これまた以前証明した内容だが、dfaとnfaも認識できる言語に差がなかったので、これら3つはどれかで認識できれば、他二つでも認識できることになる。
で、これらを使ってさらに次回別の内容も示すので、その準備と思ってもらいたい。
nfaと\(\varepsilon\)nfaの等価性
今回は、以下の定理を示す。
ある言語\(L\)について、それを認識するnfaが存在することと、それを認識する\(\varepsilon\)nfaが存在することは同値である。
冒頭でも書いたように、片方で認識できれば、もう片方でも認識できるよ、という内容だ。
では、早速示していこう。
nfaが存在⇒\(\varepsilon\)nfaが存在
まずこちらから…なのだが、勘のいい方ならすでにお気づきかもしれない。
dfaとnfaの時がそうだったように、実はnfaも\(\varepsilon\)nfaの特殊なパターンだと考えることができるのだ。
\(\varepsilon\)nfaは、あくまで空列による遷移を許容しているだけで、別にそれが無くても問題ない。
\(\varepsilon\)nfaが存在⇒nfaが存在
問題になるのはこちら。
方針は、以前やったものでいこう。
\(\varepsilon\)nfaをnfaに変換し、それらが同じ言語を認識することを示していく。
では、まずその変換を。
\(\varepsilon\)nfaを\(E = (K_E, \Sigma, \delta_E, s_0, F_E)\)とし、それを変換して作るnfaを\(N = (K_N, \Sigma, \delta_N, t_0, F_N)\)とする。
で、実際にどうやって書き換えるかだが…その前に一つ定義を。
定義:空列による遷移先の集合
\(\varepsilon\)nfaを\(E = (K, \Sigma, \delta, s_0, F)\)とし、その状態\(s \in K\)に注目する。
このとき、集合を作り出すような\(K\)から\(K\)への対応\(S\)を、状態\(s\)から空列による遷移のみで辿れる状態の集合とする。
ただ、これには\(s\)自身も含まれることとしよう。
具体例を見てみる。
前回の例で出した\(\varepsilon\)nfaを再掲する。

これで、各状態における対応\(S\)が表す集合は、以下の表のようになっている。
| 状態\(s\) | \(S(s)\) |
|---|---|
| \(s_0\) | \(\{s_0\}\) |
| \(s_1\) | \(\{s_0, s_1, s_2, s_4\}\) |
| \(s_2\) | \(\{s_2\}\) |
| \(s_3\) | \(\{s_3\}\) |
| \(s_4\) | \(\{s_4, s_0\}\) |
一つ注意で、複数回に渡って空列による遷移があった場合でも、それら全てを含む。
言い方を変えると、その状態\(s\)についての様相\((\varepsilon, s)\)からのステップが存在するような状態の集合、と捉えてもいいかもしれない。
\(\varepsilon\)nfaからnfaへの変換
この定義を使って、変換していこう。
まず、状態の集合\(K_N\)。
これは、以下のように定義する。
$$K_N = \{(s, S(s)) | s \in K_E\}$$
\(E\)内の各状態と、その\(S\)による対応先を対にしたものを、一つの状態として持つ。
次に、入力記号の集合は…これは明らかに両者とも同じなのでそもそも分けて考える必要がない。
文字で置いた時に区別してないのはそういう理由だ。
で、状態遷移関数がちょっと厄介。
ある\(N\)内の状態\((s, S(s)) \in K_N\)と、記号\(a \in \Sigma\)における状態遷移関数は以下のように定義される。
$$\delta_N((s, S(s)), a) = \{(s’, S(s’)) \in K_N | s” \in S(s), s’ \in \delta_E(s”, a)\}$$
何をしているかというと、\(S(s)\)に含まれる各状態から記号\(a\)による\(E\)内の遷移先を見て、それとその\(S\)の組を\(N\)における遷移先とする、ということ。
これでも分かりづらいかもしれないが、後で具体例を見せるので、先に初期状態と受理状態の集合も見てしまおう。
初期状態はシンプルで、\(t_0 = (s_0, S(s_0))\)。
受理状態の集合は、以下のようにしよう。
$$F_N = \{(s, S(s)) \in K_N | S(s) \cap F_E \not = \phi\}$$
組の二つ目について、その中に\(E\)における受理状態が含まれているならば、\(N\)でも受理状態にするという感じ。
ちょっと、具体的に変換をしてみよう。
上にも書いた例を変換してみる。
まず、状態の集合は…
$$\begin{eqnarray}
K_N = & \{ & \\
& & (s_0, \{s_0\}), \\
& & (s_1, \{s_0, s_1, s_2, s_4\}), \\
& & (s_2, \{s_2\}), \\
& & (s_3, \{s_3\}), \\
& & (s_4, \{s_0, s_4\}) \\
& \} &
\end{eqnarray}$$
この5つ。
状態遷移関数は飛ばして、初期状態は\(t_0 = (s_0, \{s_0\})\)。
受理状態は、今\(F_E = \{s_3\}\)なので、\(F_N = \{(s_3, \{s_3\})\}\)だ。
では、飛ばした状態遷移関数を見ていこう。
…ちょっと、状態をそのまま書くと見づらいので、添え字を合わせて\(t_i = (s_i, S(s_i))\)と表記することにしよう。
結論を書いてしまうと、以下のような感じになる。
| 現状態 | 0 | 1 |
|---|---|---|
| \(t_0\) | \(\phi\) | \(\{t_1\}\) |
| \(t_1\) | \(\{t_2, t_3\}\) | \(\{t_0, t_1\}\) |
| \(t_2\) | \(\phi\) | \(\{t_0\}\) |
| \(t_3\) | \(\{t_0\}\) | \(\{t_0, t_4\}\) |
| \(t_4\) | \(\{t_2, t_3\}\) | \(\{t_1\}\) |
…書いて思ったのだが、参考書に誤りがあった。
31ページの図2.17なのだが、\((s_4, \{s_0, s_4\})\)から\((s_3, \{s_3\})\)に向かう0による遷移が抜けている。
実際に参考書を見ている場合は気を付けよう。
さて、これらの情報を元に状態遷移図を書いてみる。
この図でも、上で定義した\(t\)の方を使って状態を表しているので、そこだけご了承願いたい。
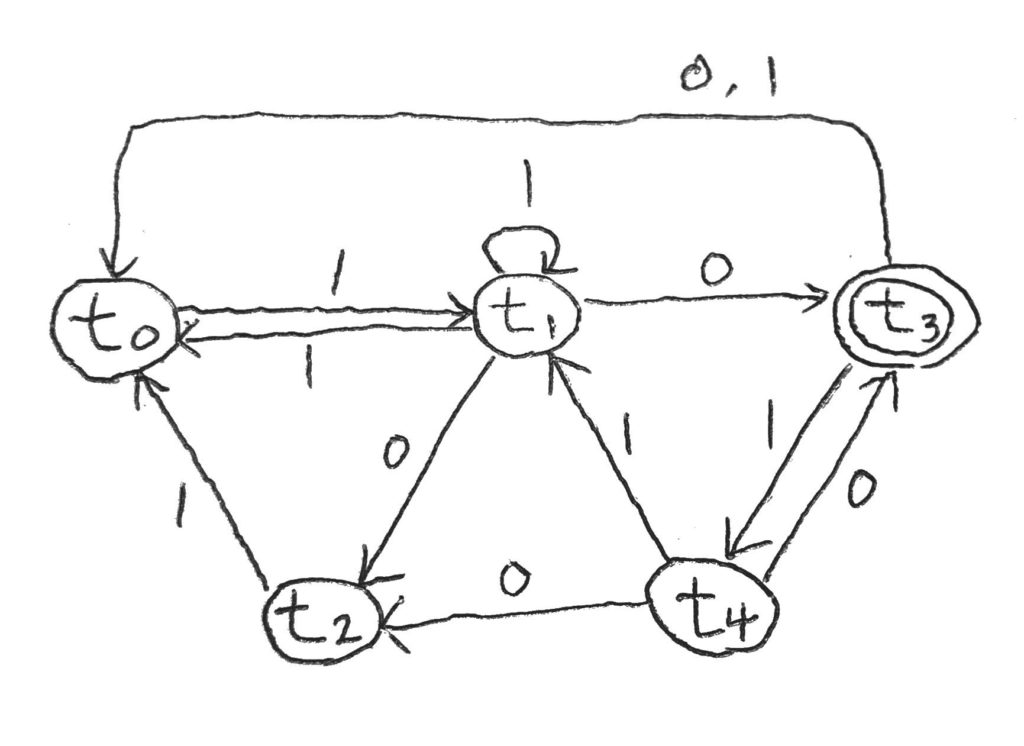
こうなった。
これが、\(\varepsilon\)nfaからnfaへの変換方法だ。
等価性の証明
さて、変換して終わりではなく、これらが同じ言語を認識することを示さなければいけない。
ここで示す内容は以下だ。
$$x \in L(E) \Leftrightarrow x \in L(N)$$
まず、右向きから示していこう。
前提となる\(x \in L(E)\)から、\(s \in F_E\)として以下のようなステップが存在する。
$$(x, s_0) \overset{*}{\Rightarrow} (\varepsilon, s)$$
この各ステップについて、二つのパターンに分けてみていこう。
まず、記号を読み込んで遷移するステップについて。
今、入力列\(x\)を分解して考えてみる。
\(a \in \Sigma\)、\(x_1, x_2 \in \Sigma^*\)として、\(x = x_1ax_2\)と置こう。
このとき、\((ax_2, s_i) \Rightarrow (x_2, s_j)\)となる2状態\(s_i, s_j \in K_E\)に注目する。
ステップの定義より、\(s_j \in \delta_E(s_i, a)\)だ。
対応\(S\)の定義より\(s_i \in S(s_i)\)なので、\(\delta_N\)の定義から以下が言える。
$$(s_j, S(s_j)) \in \delta_N((s_i, S(s_i)), a)$$
これで分かったのは、\(E\)側で記号を読み込んで遷移するようなステップの場合、\(N\)側でもその記号を読んで遷移すればいい、ということだ。
次に、空列によるステップを含むものについて。
これは連続するステップをひとまとめに考える。
上と同じように列を分解して、\(a \in \Sigma\)、\(x_1, x_2 \in \Sigma^*\)として、\(x = x_1ax_2\)とする。
このとき、\(s_1, s_2, …, s_n, s \in K_E\)について、以下のようなステップだったとしよう。
$$(ax_2, s_1) \Rightarrow (ax_2, s_2) \Rightarrow … \Rightarrow (ax_2, s_n) \Rightarrow (x_2, s)$$
つまり、\(s_1\)から\(s_n\)まで、\(\varepsilon\)による遷移で辿るようなステップだ。
その後、記号による遷移も一つ含んでいる。
このとき、ステップの定義から\(s \in \delta_E(s_n, a)\)。
また、対応\(S\)の定義から、\(s_1, s_2, …, s_n \in S(s_1)\)。
ということは、またしても\(\delta_N\)の定義から、以下が言える。
$$(s, S(s)) \in \delta_N((s_1, S(s_1)), a)$$
これが何を言っているかというと、\(E\)側で空列による遷移の連続とその直後の記号による遷移について、\(N\)側では連続した空列遷移の先頭にあたる状態から、記号による遷移先へ1回で遷移できること。
…文章だと分かりづらい。
要するに、\(E\)で仮定していたステップがある時、\(N\)では\((s_1, S(s_1))\)から\((s, S(s))\)へ記号\(a\)で遷移できるよ、ということだ。
もっと言うと、元の定義でnfaだと空列による遷移をしなかったが、今回それで辻褄が合っていることを示したわけだ。
…今書いていて、これを示す必要があったかちょっと疑問になっているが、まあ示せたので気にせず進めよう。
さて、これで同じ列を読んだときに、\(E\)側で受理状態になっていれば\(N\)側でも受理状態になっていることを示したい。
ここも、最後のステップが記号によるものか、空列によるものかで場合分けをして見てみる。
まず、最後のステップが記号によるものの場合。
この時、\(E\)側で受理状態\(s \in F_E\)に遷移したとする。
すると、\(N\)側でも状態\((s, S(s)) \in K_N\)に遷移する。
\(N\)側の受理状態\(F_N\)の定義より、\((s, S(s)) \in F_N\)が分かるので、こちらはOK。
次に、最後のステップが空列によるものの場合。
この最後にある空列による遷移の先頭を見てみる。
例えば、\(s’ \in K_E\)から\(s \in F_E\)に\(\varepsilon\)で遷移できるとしよう。
このとき、\(N\)側では最後\((s’, S(s’)) \in K_N\)に遷移する。
そして、対応\(S\)の定義より、\(s \in S(s’)\)だ。
ということで、これまた\(F_N\)の定義より、\((s’, S(s’)) \in F_N\)。
よって、こちら側は成立だ。
では、反対側を見ていこう。
\(x \in L(N) \Rightarrow x \in L(E)\)を示していく。
\(N\)側での遷移について、最終的に\((s, S(s)) \in F_N\)に到達できたとしよう。
まず、\(F_N\)の定義より、\(S(s) \cap F_E \not = \phi\)だ。
このとき、\(E\)側ではステップ\((x, s_0) \overset{*}{\Rightarrow} (\varepsilon, s)\)が存在する。
ここで、二つの場合に分けて考える。
パターン1、\(s \in F_E\)の場合。
このとき、明らかに上に書いたステップで受理状態に到達できているので、こちらはOK。
パターン2、\(s \not \in F_E\)の場合。
\(s’ \in S(s) \cap F_E \setminus \{s\}\)としておこう。
前提より\(s’ \in S(s)\)なので、状態\(s\)から空列による以下のようなステップが存在する。
$$(\varepsilon, s) \overset{*}{\Rightarrow} (\varepsilon, s’)$$
同じく前提から\(s’ \in F_E\)なので、こちらも受理状態までのステップが存在することが分かった。
このパターンで全てなので、左向きも成立。
以上で、\(\varepsilon\)nfaとnfaが同じ言語を認識できることが示せた。
おわりに
書いている方もなかなか混乱しやすいくらいには複雑な内容だった。
しかし、これでdfa、nfa、\(\varepsilon\)nfaそれぞれで認識できる言語に差がないことが示せたことになる。
次回は、さらに\(\varepsilon\)nfaと、だいぶ前にやった正規表現で認識できる言語に差がないことを示すことにしよう。
示す内容ががらっと変わるので、不安なら正規表現を復習しておくといいだろう。
2021/1/9追記
次回の内容を投稿した。
まず、正規表現で生成できる言語について、その言語を認識する\(\varepsilon\)nfaが存在することを示した。
こちら側は簡単だが、反対方向が複雑になりそう…



コメント