本シリーズでは、以下の本に沿って解説を書いている。

前回は、cfgを考える時に便利な最左導出と導出木を解説した。
まだ便利になる状況がそんなに出てきていないが、今後出てくる…はず。
以下がその記事だ。
さて、今回は以前扱っていた正規言語との関係について見ていこう。
いきなり結論を書いてしまうが、正規言語は文脈自由言語の部分集合になっている。
それを、今回示していこう。
なお、正規言語が分からない方は、dfa、nfa、\(\varepsilon\)nfa、正規表現あたりを復習しよう。
今回証明する内容
改めて、今回証明していく内容を出そう。
ある言語\(L\)が正規言語であるならば、その言語\(L\)は文脈自由言語である、というもの。
これを示す方針は、シンプルにdfaをcfgに変換するものでいこう。
まず、dfaをcfgに変換する方法を紹介する。
そして、それらが構成する言語に差がないことを示す、という内容だ。
…念のため、この方針で問題ない理由だが、dfaが認識する言語が正規言語、cfgで生成できる言語が文脈自由言語であったことを思い出そう。
dfaからcfgへの変換
最初にこれを見ていこう。
変換元となるdfaを、\(M = (K, \Sigma, \delta, S_0, F)\)とする。
以前dfaの状態は\(s_0, s_1, …\)のように小文字で置いていたが、今回は\(S_0, S_1, …\)というように大文字にしておく。
名前の書き換えだけなので問題ない。
そして、変換後のcfgを\(G = (V, \Sigma, P, S)\)としておこう。
まず、\(V\)については、\(V = K\)としてあげる。
そのままdfaの状態を使ってもよかったのだが、一応慣れている文字に置き換えさせてもらった。
ちょっと順番が前後するが、先に開始記号については\(S = S_0\)だ。
次に終端記号の集合、これはdfaの入力記号の集合そのままでいい。
さて、問題となるのは生成規則をどうするかだ。
これについて、dfa側である状態\(S_i \in K\)、記号\(a \in \Sigma\)による遷移先が\(\delta(S_i, a) = S_j\)となっているとき、以下の生成規則を加える。
$$S_i \rightarrow aS_j$$
そして、さらに\(S_F \in F\)という状態について、以下の生成規則を加えてあげる。
$$S_F \rightarrow \varepsilon$$
これで完成だ。
具体例で見てみよう。
dfaの解説時に具体例として出したもので見ていこう。
dfa\(M\)の内訳は以下の通り。
- \(K = \{S_0, S_1, S_2, S_3\}\)
- \(\Sigma = \{0, 1\}\)
- \(F = \{S_0\}\)
状態遷移関数は以下の表だ。
| 現状態 | \(0\)による遷移先 | \(1\)による遷移先 |
|---|---|---|
| \(S_0\) | \(S_1\) | \(S_2\) |
| \(S_1\) | \(S_0\) | \(S_3\) |
| \(S_2\) | \(S_3\) | \(S_0\) |
| \(S_3\) | \(S_2\) | \(S_1\) |
状態遷移図も出しておこう。
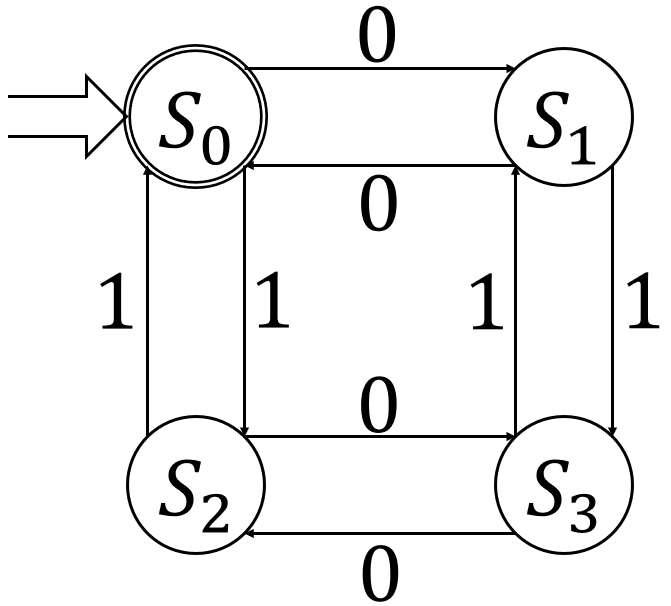
では、ここからcfg\(G\)を作っていく。
まず、簡単なところから。
- \(V = \{S_0, S_1, S_2, S_3\}\)
- \(\Sigma = \{0, 1\}\)
- \(S = S_0\)
では、生成規則\(P\)を見ていこう。
まず、変数\(S_0\)について。
dfaではこれに記号\(0\)を入力すると\(S_1\)に遷移するので…
$$S_0 \rightarrow 0S_1$$
という生成規則ができる。
次に、記号\(1\)を入力すると\(S_2\)に遷移するので…
$$S_0 \rightarrow 1S_2$$
こんな感じで出来上がる。
また、今\(S_0\)は受理状態なので…
$$S_0 \rightarrow \varepsilon$$
これも該当する。
こんな感じでどんどん作っていくと…
- \(S_0 \rightarrow \varepsilon\)
- \(S_0 \rightarrow 0S_1\)
- \(S_0 \rightarrow 1S_2\)
- \(S_1 \rightarrow 0S_0\)
- \(S_1 \rightarrow 1S_3\)
- \(S_2 \rightarrow 0S_3\)
- \(S_2 \rightarrow 1S_0\)
- \(S_3 \rightarrow 0S_2\)
- \(S_3 \rightarrow 1S_1\)
この9個が出来上がる。
これで、変換後のcfgが完成、というわけだ。
同じ言語であることの証明
さて、作って終わりではない。
これらによってできる言語が同じであることを証明しなければいけない。
式で書くと以下の通り。
$$L(M) = L(G)$$
これは集合のイコールなので、例によって以下の形に書き直す。
$$x \in L(M) \Leftrightarrow x \in L(G)$$
では、見ていこう。
右向き
まず、\(x \in L(M) \Rightarrow x \in L(G)\)を示していく。
\(|x| = n\)として、n個の記号\(a_1, a_2, …, a_n \in \Sigma\)を使って\(x = a_1a_2…a_n\)と置いておく。
\(n\)を出しているが、今回は帰納法ではないので注意。
では、この記号たちを初期状態から順番に入れていこう。
dfa側では…
- \(\delta(S_0, a_1) = S_1\)
- \(\delta(S_1, a_2) = S_2\)
- …
- \(\delta(S_{n – 1}, a_n) = S_n \in F\)
となっているとしよう。
もちろんだが、この状態の中には重複しているものがあっていい。
これについて、cfg側ではどうなっているかを見ていく。
まず、上の変換方法から\(S_0 \rightarrow a_1S_1\)が存在するので…
$$S_0 \Rightarrow a_1S_1$$
となる。
次に、\(S_1 \rightarrow a_2S_2\)が存在するので…
$$a_1S_1 \Rightarrow a_1a_2S_2$$
このようにステップを作ることができる。
これを繰り返していくと、最終的に…
$$a_1a_2…a_{n-1}S_{n-1} \Rightarrow a_1a_2…a_{n-1}a_nS_n$$
こんなステップになる。
そして、\(S_n \in F\)から、\(S_n \rightarrow \varepsilon\)という生成規則があるので、これを使って…
$$a_1a_2…a_{n-1}a_nS_n \Rightarrow a_1a_2…a_{n-1}a_n \varepsilon$$
この導出が可能だ。
あとは単なる式変形。
$$\begin{eqnarray}
a_1a_2…a_{n-1}a_n \varepsilon & = & a_1a_2…a_{n-1}a_n \\
& = & x
\end{eqnarray}$$
ということで、\(x\)を生成できたことになる。
以上で\(x \in L(G)\)だと分かったので、こちら側は証明完了だ。
…ちなみに、今\(M\)に受理状態が存在する前提で話を進めていた。
受理状態が存在しない場合については、まず\(L(M) = \phi\)となる。
このとき、上の変換方法で得られたcfg\(G\)については、生成規則の結果、必ず変数を含むことになる。
常に変数を含むということは、どんな列も生成することができない。
そもそも列を生成するときは、変数を含まない形にしなければならなかったことを思い出そう。
ということで、こちらも任意の列を生成しない…\(L(G) = \phi\)となるので問題ない。
左向き
今度は、\(x \in L(G) \Rightarrow x \in L(M)\)を示そう。
上では最後に見ていた、言語が空集合の場合…\(L(G) = \phi\)を先に見ておく。
このとき、上で見たように全ての生成規則の右側は変数を含んでいる。
そして、今回の変形方法によれば、変数を含まないような生成規則はdfa側で受理状態が存在する時に出来上がる。
それがないということは、受理状態も空集合になっている。
つまり、dfaも任意の列を受理せず、\(L(M) = \phi\)となる。
以上で\(L(G) = \phi\)の時は成立すると分かったので、以降は\(L(G) \not = \phi\)を前提として話を進めていこう。
まず、前提から以下の導出が存在することが分かる。
$$S_0 \overset{*}{\Rightarrow} x$$
さて、今cfg\(G\)の生成規則で、生成先が空集合でないものに注目する。
これも変換方法から言えることだが、この生成規則は、\(A, B \in V\)と\(a \in \Sigma\)を使って必ず以下のような形になっている。
$$A \rightarrow aB$$
これを使って\(x\)の導出を分解していこう。
さっきと同じように、\(|x| = n\)として、n個の記号\(a_1, a_2, …, a_n \in \Sigma\)を使って\(x = a_1a_2…a_n\)と置く。
このとき、以下のように書き表せる。
$$\begin{eqnarray}
S_0 & \Rightarrow & a_1S_1 \\
& \Rightarrow & a_1a_2S_2 \\
& … & \\
& \Rightarrow & a_1a_2…a_nS_n = xS_n
\end{eqnarray}$$
ここで最後に出てきた変数\(S_n\)だが、この前までがそのまま\(x\)になっている。
つまり、\(S_n \rightarrow \varepsilon\)という生成規則が存在する。
そして、その前までのステップから、以下のような生成規則も存在する、ということになる。
- \(S_0 \rightarrow a_1S_1\)
- \(S_1 \rightarrow a_2S_2\)
- …
- \(S_{n – 1} \rightarrow a_nS_n\)
では、変換方法と照らし合わせて、dfa側の状態遷移を見てみる。
すると、以下のような定義がされていることが分かる。
- \(\delta(S_0, a_1) = S_1\)
- \(\delta(S_1, a_2) = S_2\)
- …
- \(\delta(S_{n – 1}, a_n) = S_n\)
また、\(S_n \rightarrow \varepsilon\)から、\(S_n \in F\)だ。
もうここまで来ればお分かりだろう。
dfaで、初期状態から\(x = a_1a_2…a_n\)を入力すると…
$$\begin{eqnarray}
\delta(S_0, x) & = & \delta(S_0, a_1a_2a_3…a_n) \\
& = & \delta(S_1, a_2a_3…a_n) \\
& … & \\
& = & \delta(S_{n – 1}, a_n) \\
& = & S_n \in F
\end{eqnarray}$$
こんな感じで、受理状態\(S_n\)にたどり着く。
よって、\(M\)で列\(x\)が受理されたので、\(x \in L(M)\)が言えたことになり、こちらも成立。
以上で、\(L(M) = L(G)\)が示せた。
おわりに
今回は証明パートで、正規言語は文脈自由言語でもあることを示した。
また、以前の具体例で文脈自由言語は正規言語ではない言語も生成できることが分かっている。
これで、文脈自由言語は正規言語よりも幅が広い…言い換えると、dfaや正規表現などよりもcfgの方が生成できる言語が多いことが分かった。
では、どんな言語もcfgで生成できるのだろうか…と言われると、実はこれも不可能な言語が存在する。
その内容…に進む前に、もう一つ解説したいことがあるので、次回はそれに進もう。
チョムスキー標準形、グライバッハ標準形という二つの形だ。
今回の内容は必要ないが、cfgの基本はしっかり抑えてから進んでいこう。
2020/1/30追記
次回の内容を更新した。
ちょっと想像以上に記事が長くなってしまったので、まずはチョムスキー標準形のみを解説している。
グライバッハ標準形にも使うので、変換方法は是非押さえておきたい。



コメント