本シリーズは、論理回路で電卓を作ろうと思い、そのために勉強した結果を残しているものだ。
前回は、XOR、NAND、NORの3つと、論理演算について解説した。
今後も常に使うものたちなので、それを通して慣れていくといいだろう。
以下がその記事だ。
さて、今回からいよいよ実践に近い話をしていこう。
第2回、2進数のところで加算だけ実装すれば、他の3演算は可能だということを書いた。
今回は、その加算を実際に実装してみよう。
これを構成する回路には名前がついており、2種類あってそれぞれ半加算器、全加算器と呼ぶ。
この加算器を使って、実際に4桁の加算を行う回路を作る。
そのまま、減算も行えるところまで実装してみよう。
2つの加算器
さて、加算を行う回路は、その名の通り加算器という名前がついている。
もう冒頭にも書いているが、半加算器、全加算器という2つの加算器があるので、その詳細をそれぞれ見ていこう。
半加算器
まずはこの半加算器から。
これは、1桁同士の2進数を加算した結果を出力する組合せ回路だ。
…とはいえ、1桁の2進数の加算は4パターンしかない。
以下にそのパターンを全部出そう。
なお、括弧と後ろに進数を表記していないが、2進数で考えて欲しい。
$$\begin{eqnarray}
0 + 0 & = & 0 \\
0 + 1 & = & 1 \\
1 + 0 & = & 1 \\
1 + 1 & = & 10
\end{eqnarray}$$
これだけだ。
では、これを回路で実現してみよう。
まず、入力はもちろん2つの1桁の2進数。
そして、出力も2つになる。
一つは計算した桁の結果、もう一つは桁上がりだ。
よく、同じ桁の出力を\(S\)(Sum)、桁上がりの出力を\(C\)(Carry)と表すので、ここでも同じ表記を使う。
…桁上がりと書いているが、シンプルに上の桁の結果として考えてもらって構わないだろう。
入力を\(I_1, I_2\)としたときの真理値表を以下に示す。
| \(I_1\) | \(I_2\) | \(S\) | \(C\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
…どこかで見覚えがあるだろう。
\(S\)は2つの入力のXORで表現でき、\(C\)は2つの入力のANDで表現できる。
つまり、ブール代数で表現すると以下の通り。
$$\begin{eqnarray}
S & = & I_1 \oplus I_2 \\
C & = & I_1 I_2
\end{eqnarray}$$
そして、これで回路を組むと以下のようになる。
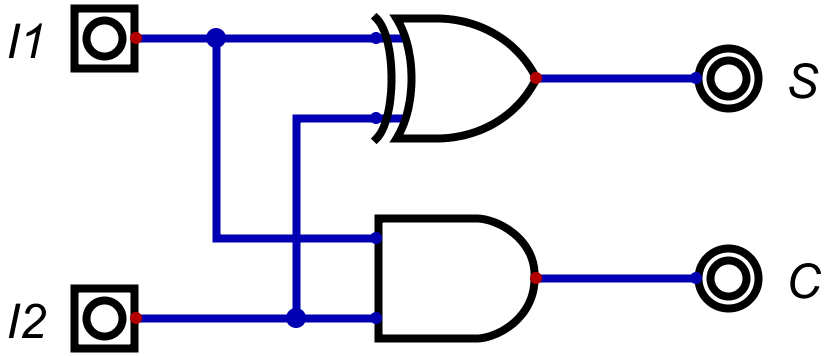
ここで、2つほど使用しているシミュレータに関する補足を。
左側にある、四角の中に丸があるものは入力を、右にある二重丸は出力を表している。
というわけで、これで1桁同士の加算は完成だ。
全加算器
次に、この全加算器というもの。
一体何をするものかというと、これも1桁同士の2進数を加算するもの…なのだが、追加でもう一つ考えることがある。
何かというと、下の桁からの桁上がりだ。
つまり、入力は3入力になる。
2つは該当の桁の2進数\(I_1, I_2\)と、残り一つは下の桁からの桁上がり\(C’\)。
出力は…半加算器と同じく、該当桁の結果\(S\)と上位桁への桁上がり\(C\)。
二つでいい理由は、3つの1桁2進数の加算結果の最大値は10進数で書くと3、2進数で書くと11だから。
ここまで表現できれば問題ないので、2出力のままで済んでいる。
パターンは全部で8パターンとなり、真理値表を以下に挙げよう。
なお、出力を見やすいよう、\(C\)、\(S\)の順番にしておこう。
| \(I_1\) | \(I_2\) | \(C’\) | \(C\) | \(S\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
では、これを実際に組んで…といきたいところだが、少し待って欲しい。
確かに、これをそのまま考えても組むことはできるが、その前に意味を考えてみよう。
これは、まず2つの入力\(I_1, I_2\)をそのまま足し、その結果と下からの桁上がり\(C’\)をもう一回足す、と考えられる。
つまり、シンプルな加算を2回行っている、と捉えられるのだ。
このシンプルな加算は、上でやった半加算器で実現できている。
ということは、それを2つ繋げることで、この全加算器も実現できる、ということになる。
入力を\(I_1, I_2\)とした時の半加算器の真理値表を再掲しておこう。
| \(I_1\) | \(I_2\) | \(S_1\) | \(C_1\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
この半加算器が一つ目と言う意味で、この出力をそれぞれ\(S_1, C_1\)としている。
では、次にこの\(S_1\)と下からのキャリー\(C’\)の組合せで、二つ目の半加算器の出力\(S_2, C_2\)を求めてみよう。
| \(S_1\) | \(C’\) | \(S_2\) | \(C_2\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
まあ、入出力の記号が変わるだけだ。
では、この二つを組み合わせて、ついでに全加算器全体の期待する出力\(S, C\)も入れて再度一つの表に直してみる。
| \(I_1\) | \(I_2\) | \(C’\) | \(C_1\) | \(S_1\) | \(C_2\) | \(S_2\) | \(C\) | \(S\) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
今、この\(S\)と\(C\)をどう求めるかを考えたい。
…まあ、\(S\)は二つ目の半加算器の出力\(S_2\)そのままなので問題ないだろう。
残る問題は、上位桁へのキャリー\(C\)。
これを注意深く見てみると、どうやら\(C_1\)と\(C_2\)のいずれかが1なら、\(C\)も1になっていそうだ。
というわけで、単にORを取ればいいので、\(C\)はブール代数で表すと以下の通り。
$$C = C_1 + C_2$$
よく見ると、\(C_1\)と\(C_2\)がともに1の場合がないので、XORでも実現ができるのだが…まあ、普通はORを使うので覚えておこう。
これで回路を組むと以下のようになる。
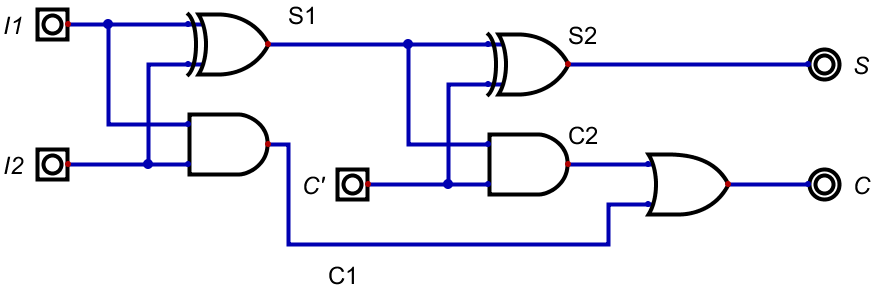
これで、各桁における加算は問題なく行えるようになった。
ちなみに、余談ではあるのだが、半加算器2つ(+OR)で全加算器を実装できるということは、全加算器の半分が半加算器だ、というところから半加算器、全加算器という名前らしい。
n桁の2進数の加算
では、ここまで出した二つの加算器を組み合わせて、n桁の2進数の加算を実装しよう。
今回は入力・出力共に4桁で説明するが、同じことの繰り返しで何桁でも実現可能だ。
さて、これ以降毎回加算器の中身を全て書いていると図が大きくなってしまうので、それぞれ以下で示すことにする。
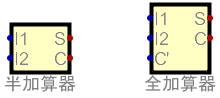
この中身は、それぞれ上に出したものそのままとなっているので、分からなければそちらを見るようにしよう。
入出力の記号も同じに合わせているので、それで確認してみてほしい。
では、4桁の2進数二つを入力し、その合計を出力する回路を作っていこう。
とはいえ、非常に簡単。
まず、各桁の加算器への入力\(I_1,I_2\)に、該当する桁の入力を入れる。
そして、加算器の出力\(S\)をその桁の結果、\(C\)を上位桁の\(C’\)に繋げればいい。
ここで、一つ注意しなければならないのが、一番下の桁だ。
ここは、下からの桁上がりがないので、半加算器を使う。
下から2桁目以降は、常に下からの桁上がりがある可能性があるので、全部全加算器になる。
ということで、サクッと組んでみたのが以下の論理回路図だ。
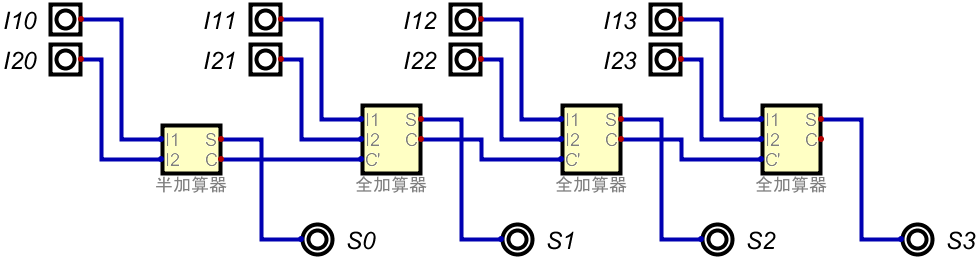
入力は計8個、2つの4桁2進数。
一つ目の2進数を\(I_1 = I_{13} I_{12} I_{11} I_{10}\)、二つ目の2進数を\(I_2 = I_{23} I_{22} I_{21} I_{20}\)と表している。
出力は、もちろん加算した結果の4桁の2進数\(S = S_3 S_2 S_1 S_0\)だ。
最上位からのキャリーは使わないので、どこにも繋げていない。
これで4桁の加算が実現でき、桁が増えたとしても同じように増やしていけばOKだ。
…本当は、これだと結果が出るまでに通るANDやORなどが多く、処理に時間がかかってしまう。
特に上位の桁は、それまでの桁の計算が終わらないと始められない。
そこで、先に下からの桁上がりがあるかを確認するような回路を別途作成して、時間を減らそうという考え方もあるのだが…そこまでやっていると記事が長くなってしまうので、一旦パスさせてもらう。
まだどこかで解説するかは決めていないが、気になれば先に調べてみるといいだろう。
復習:2の補数
今、2進数同士の加算ができるようになった。
ここで、2の補数というものを考えれば減算もできる、ということを第2回でやったと思う。
この後使うので、少し復習しておこう。
2の補数とは、簡単に言うと桁が制限されている2進数で、負の数を表現する考え方だ。
例えば、4桁で制限されているとき。
これは、5桁目以降は無視される。
それを上手く利用し、足したら0になる数を負の数として考えよう、というものだ。
\((0011)_2\)という数の時、何かを足して\((10000)_2\)となれば、最上位が無視され\((0)_2\)となる。
この何かを\(x\)とすると…
$$\begin{eqnarray}
0011 + x & = & 10000 \\
x & = & 10000 – 0011 \\
x & = & 1111 – 0011 + 1 \\
x & = & 1100 + 1 \\
x & = & 1101
\end{eqnarray}$$
ということで、この\((1101)_2\)が、\((0011)_2\)に対応する負の数、10進数で言えば-3になる。
この求め方も簡単だった。
まず元の数の各桁の0と1を全て入れ替え、その後に1を足せばよかった。
実際に\((0011)_2\)の0と1を入れ替えると\((1100)_2\)、これに1を足せば\((1101)_2\)で同じになるだろう。
ということで、これを先に考えて加算器に入力すれば、減算が実現できる。
なお、これで表現できる範囲は、制限をn桁とすると\(2^{n-1} – 1\)以下、\(-2^{n-1}\)以上だった。
また、負の数かどうかの見分け方は、最上位の桁が0なら正の数、1なら負の数だったことも思い出そう。
オーバーフロー
では、ここから加算器の話に戻る。
ここでは2進数の桁制限を4桁、符号も考えることにしよう。
つまり、\((0111)_2 = (7)_{10}\)、\((1000)_2 = (-8)_{10}\)だ。
ここで、例えば10進数でいう4 + 4を、加算器で計算してみる。
その結果は以下の通りだ。
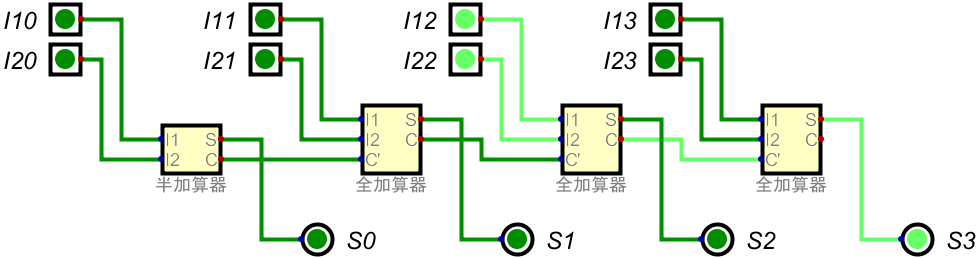
結果、\((1000)_2\)となった。
まあ、\((0100)_2 + (0100)_2\)なので当然だろう。
…さて、\((1000)_2\)の最上位は1だ。
つまり、これは負の数で、\((-8)_{10}\)となっている。
正の数同士を足したはずなのに、結果は負の数になってしまっている。
明らかにおかしいだろう。
このように、本来得られるべき結果と異なる結果が得られてしまう現象を、オーバーフローという。
これが起こる原因は、もうなんとなくお分かりかと思う。
今計算した\((4)_{10} + (4)_{10}\)は結果が\((8)_{10}\)、4桁で表現できる範囲を超えている。
ということで、この限界を超えたものが表現できず、おかしなことになってしまうのだ。
そして、現時点の4桁加算器では計算結果しか表示されないので、ぱっと見でこれが起こっているかが分からない。
それを判定して、オーバーフローが起こったら1を出力することを考えてみよう。
まず、意味的に考えると、計算結果が\((7)_{10}\)より大きい、あるいは\((-8)_{10}\)より小さい場合に発生する。
が、そもそも入力できる範囲もこの中に納まっているため、計算結果が\((7)_{10}\)より大きくなるのは正の数同士の加算、\((-8)_{10}\)より小さくなるのは負の数同士の加算だと分かる。
そして、上でやったように、\((7)_{10}\)より大きくなると、その計算結果は負になる。
ちなみに、\((-8)_{10}\)より小さくなった場合は、やはり計算結果も正になる。
試しに、\((-5)_{10} + (-4)_{10}\)で試してみよう。
\((-5)_{10} = (1011)_2\)、\((-4)_{10} = (1100)_2\)なので…
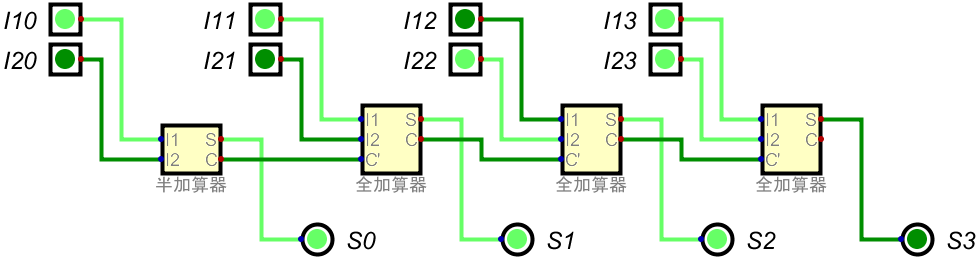
となり、結果は\((0111)_2 = (7)_{10}\)で正しく(?)おかしいことになっている。
ということは、だ。
結果がおかしい時は符号が想定される結果と異なっている、ということに注目すると、この入出力の符号を見ればオーバーフローが分かりそうだ。
そこで、入出力の符号と、オーバーフローの発生有無を以下の表にまとめてみた。
| \(I_1\)の符号 | \(I_2\)の符号 | \(S\)の符号 | オーバーフロー |
|---|---|---|---|
| + | + | + | |
| + | + | – | 発生! |
| + | – | + | |
| + | – | – | |
| – | + | + | |
| – | + | – | |
| – | – | + | 発生! |
| – | – | – |
さて、\(I_1\)、\(I_2\)、\(S\)の符号は、それぞれの最上位桁が0ならプラス、1ならマイナスだ。
そして、オーバーフローが発生したら1を\(E\)として出力すると考えると、以下の真理値表を作れる。
| \(I_{13}\) | \(I_{23}\) | \(S_3\) | \(E\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
これで、出力\(E\)は以下のブール代数で示す形で実現が可能だ。
$$E = \overline{I_{13}} \overline{I_{23}} S_3 + I_{13} I_{23} \overline{S_3}$$
…もうちょっと考えてみよう。
よく見ると、\(E\)が1になる時は、必ず\(I_{13}\)と\(I_{23}\)が同じ時。
これは、XORのNOTだ。
そして、それらいずれかと\(S_3\)が異なっている時に\(E\)が1となる。
つまり、以下の形に書き直すことができる。
$$E = ( \overline{I_{13} \oplus I_{23}} ) \cdot ( I_{13} \oplus S_3)$$
式の後半、\(S_3\)とXORを取っている\(I_{13}\)は、\(I_{23}\)でも構わない。
これを組んだ論理回路図が以下になる。

これで、出力\(E\)が1なら、結果がおかしいんだなというのが分かるようになった。
…なんとなく、最上位桁からのキャリーを使ってもできそうな気はしている。
そっちは今後やる気があればチャレンジし、上手くいけばどこかのオマケで補足することにしよう。
加減算器の作成
さて、ここまでで加算が行えるようになっていた。
そして、減算もあらかじめ手計算で負の値を求め、それを入力することで実現できた。
…しかし、その負の値を求めるところも回路で行わせたいだろう。
そこで、新たに入力\(M\)というものを用意し、これを使って加算か減算かを切り替えることを考えてみたい。
この減算の時、入力する二つの4桁2進数のうち、一つ目から二つ目を引くという形にしよう。
また、入力\(M\)が0の時は加算、1の時は減算だとする。
つまり、\(M\)が0ならシンプルに\(I_1 + I_2\)を、\(M\)が1なら今度は\(I_1 – I_2\)を計算する、という形だ。
\(M\)はモード(Mode)の頭文字のつもりでつけたが、マイナス(Minus)の頭文字と考えてもいいだろう。
さて、さっき復習した通り、ある数の2の補数は以下の手順で求めることができた。
- 各桁の0と1を入れ替える
- 1を足す
このうち、まず一つ目について見てみる。
\(M\)が0ならそのまま、1なら2の補数に変換したい…つまり\(I_2\)の各桁を反転させたい。
ようするに、\(I_2\)の各桁は以下のような形で加算器に入力されることになる。
| 元の\(I_{2n}\) | \(M\) | 加算器に入力される\(I_{2n}\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
これは、XORそのものだ。
ということで、まずは\(I_2\)の各入力に\(M\)とのXORを入れてあげれば各桁反転はOKだ。
次に、1を足す部分。
今、加算器の最下位の桁は半加算器を使っており、シンプルに2つの入力された数字のみを加算していた。
やり方としては、もう一つ半加算器を挟み、加算する数を増やす、というのが一つ挙げられる。
…が、これは全加算器と同じ考え方だった。
つまり、この半加算器を全加算器と入れ替えてあげれば、3数の加算が可能となる。
全加算器への入力は\(C’\)…下位からのキャリーとなっているが、内部動作的にはシンプルに3数を加算しているだけなので、そこに2の補数を作るための1を足しても問題ない。
では、そこに何を入力するかだが…まあ、\(M\)が0なら0を、1なら1を入れればいいだろう。
つまり、この最下位を計算する全加算器への入力\(C’\)は、そのまま\(M\)となる。
これで、先ほどの4桁加算器を拡張し、4桁加減算器を組んだ結果が以下の通りだ。
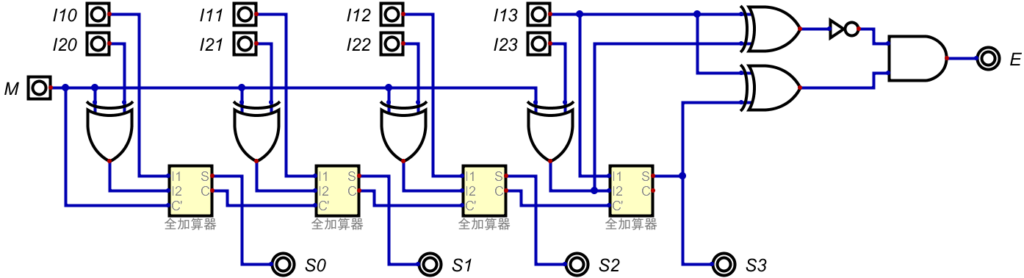
以上で、4桁分の加減算器が完成した。
まだ乗算、除算はできないが、少しだけ電卓っぽくなった…ような気がする。
おわりに
今回は、実際に2進数の計算を始めた。
まだ本シリーズは数回しかやっていないが、それだけでもここまでのものは作れるのだ。
元がシンプルなだけに、組み合わせが非常に強力なのが分かってもらえたと思う。
もし、ご自身でもシミュレータをお持ちなら、これらを実際に作って計算してみるのも面白いだろう。
さて、次回は10進数と絡めてみよう。
今、入出力はともに2進数でやっていた。
2進数で計算する電卓が最終目標ならこれでいいのだが…やはり、実際に10進数で入出力できた方が分かりやすい。
つまり、10進数で入力したものを2進数に直して計算、その結果を再度10進数に直すという仕組みが必要になる。
その中で、次回は2進数の結果を10進数に直す、という部分をやってみようと思う。
その際、効果的に回路を小さくするための手法も幾つか紹介するつもりだ。
やりたいことが多くなると、それだけ回路も大規模になる。
少しでも規模を抑えるためにも、細かいところをしっかり考えていこう。
2021/12/5追記
次回の内容を更新した。
予定通り、2進数を入力し、10進数として出力する回路を作成した。
その過程で、回路を簡略化する手法のうち、カルノー図とクワイン・マクラスキー法というものも解説している。
そのまま愚直に組むとかなり大規模になってしまうので、できる限り簡略化していこう。





コメント