本シリーズは、論理回路で電卓を作ろうと思い、そのために勉強した結果を残しているものだ。
前回は、フリップフロップが非同期という形で組まれていたことによる問題を解決するため、同期という形を解説した。
基本、この同期式のフリップフロップはシミュレータ側で用意されていることが多く、回路の中身を理解する必要はそこまでない。
が、クロックがどういう時に、入力や現状態を反映させるかという部分は非常に重要なので、そこだけは理解しておこう。
また、前回も書いたが、今後は特に断りがない限り、フリップフロップと言ったらポジティブエッジトリガ方式で組まれたものを使用することにする。
以下がその記事だ。
さて、まだ具体的にはフリップフロップを使っていなかった。
そこで、今回はそれを使って、カウンタと呼ばれる回路を組んでみよう。
これができれば、四則演算の残り乗算、除算ができるようになる。
今回でカウンタを作成し、次回で乗算、除算を実装する、という流れで進めていこう。
カウンタ
まずはこいつの正体から。
とはいえ、名前からどんな動作をするか、もう予想がつくだろう。
カウンタとは、ある条件を満たすごとに状態が次々と変化していく回路のこと。
この中でも色々と種類があるが…今回は、二つのカウンタを紹介しよう。
カウンタ
全く同じ名前だが、区別するならアップカウンタと呼ぶべきだろうか。
これは、条件を満たすごとに2進数の数が増えるように状態が変化する回路だ。
例えば、クロックが0から1になる度に数が増えるようにする場合、4出力(\(O_3 O_2 O_1 O_0\))は…
| クロック立ち上がり回数 | \(O_3\) | \(O_2\) | \(O_1\) | \(O_0\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| … | … | … | … | … |
| 15 | 1 | 1 | 1 | 1 |
| 16 | 0 | 0 | 0 | 0 |
こんな感じになる。
では、早速これを組んでみよう。
一番下の位から順に見てみる。
まず、\(O_0\)について、これはクロックのたびに0と1が反転している。
そのため、ここはJKフリップフロップを用いて両方に1を、あるいはTフリップフロップに1を入力しておけば問題ないだろう。
次に、\(O_1\)について。
ここは、\(O_0\)が0ならクロックの立ち上がりが来ても状態は変化せず、1なら現状態を反転させる、という形になっている。
そのため、JKフリップフロップの両入力に、\(O_0\)をそのまま入力すれば想定した動きになりそうだ。
そのまま、\(O_2\)に進もう。
今度は、\(O_1\)の状態が1の時…だけではなく、\(O_0\)の状態も1の時、つまりこの二つのANDが1なら状態を反転させるとよさそう。
さて、パターンが分かってきただろうか。
2進数的に考えてみよう。
各出力を2進数の各桁とみなして、1を足していくことを考えてみる。
すると、一番下の桁は0と1を交互に繰り返すことになる。
下から2番目の桁は、一番下の桁が1の時に0と1を反転させる。
下から3番目の桁は、それまでの桁が全て1の時に0と1を反転させる。
…つまり、4番目は、1から3番目までの桁が全て1なら、また反転させればいい、というわけだ。
よって、\(O_3\)は、\(O_0\)から\(O_2\)のANDを、両入力に入れてあげればいいのだ。
一旦ここまでにして、回路を組んでみよう。
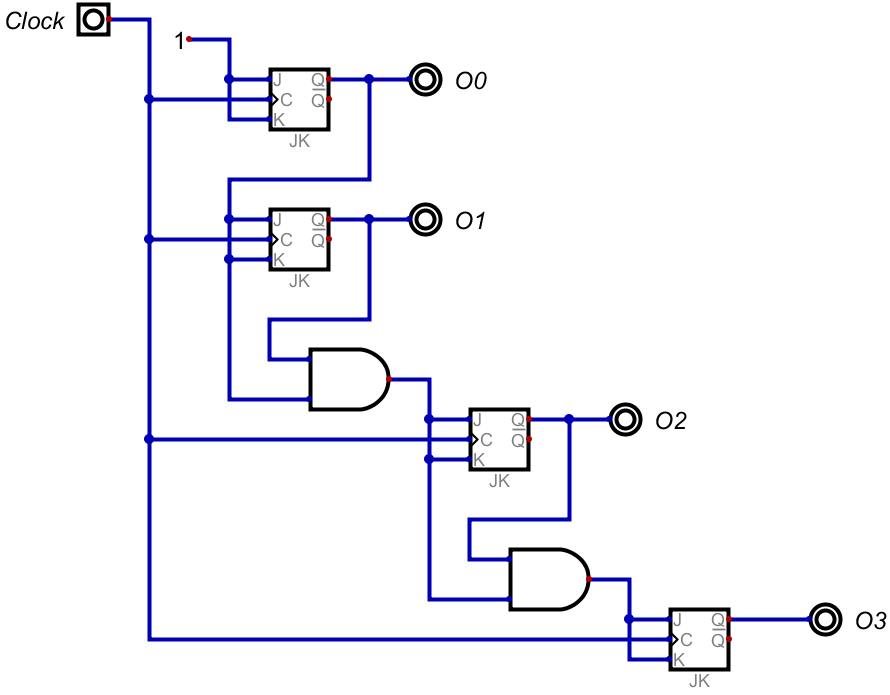
これで、4つの出力を行うアップカウンタの完成だ。
もちろん、同じ考え方で5つ目、6つ目…の出力を増やすこともできる。
使う場合には、今どこまでのカウンタが必要かを考えて組むようにしよう。
ダウンカウンタ
次に、ダウンカウンタというもの。
まあ、これも名前から分かりやすく、今度は特定の条件で2進数を1ずつ減らすよう変化するカウンタだ。
アップカウンタと同じように状態の変化を表すと、以下の表のようになる。
| クロック立ち上がり回数 | \(O_3\) | \(O_2\) | \(O_1\) | \(O_0\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| … | … | … | … | … |
| 15 | 0 | 0 | 0 | 1 |
| 16 | 0 | 0 | 0 | 0 |
| 17 | 1 | 1 | 1 | 1 |
では、同じく一番下の桁から見ていこう。
\(O_0\)は、アップカウンタと同じくクロック1回ごとに状態が反転しているので、同じく両入力に1を入れておけばいいだろう。
次に、\(O_1\)は…\(O_0\)が0の時に反転している、と捉えられる。
つまり、今度は\(O_0\)のNOTを入力することになる。
そして、\(O_2\)はやはり\(O_1\)、\(O_0\)がともに0の場合だ。
ということで、\(O_2\)への入力は、\(O_1\)と\(O_0\)のNORということになる。
…が、回路を組む上では、ちょっと変形をしておこう。
$$\overline{O_0 + O_1} = \overline{O_0} \cdot \overline{O_1}$$
ド・モルガンの定理で、先にNOTにして、それをANDで取るという形に変えただけだ。
同じように、\(O_3\)も\(O_0\)から\(O_2\)が全て0なら反転させるので、入力ももちろん\(O_0\)から\(O_2\)までのNORだ。
こっちも変形しておこう。
$$\overline{O_0 + O_1 +O_2} = \overline{O_0} \cdot \overline{O_1} \cdot \overline{O_2}$$
これも、同じく回路を組んでみる。
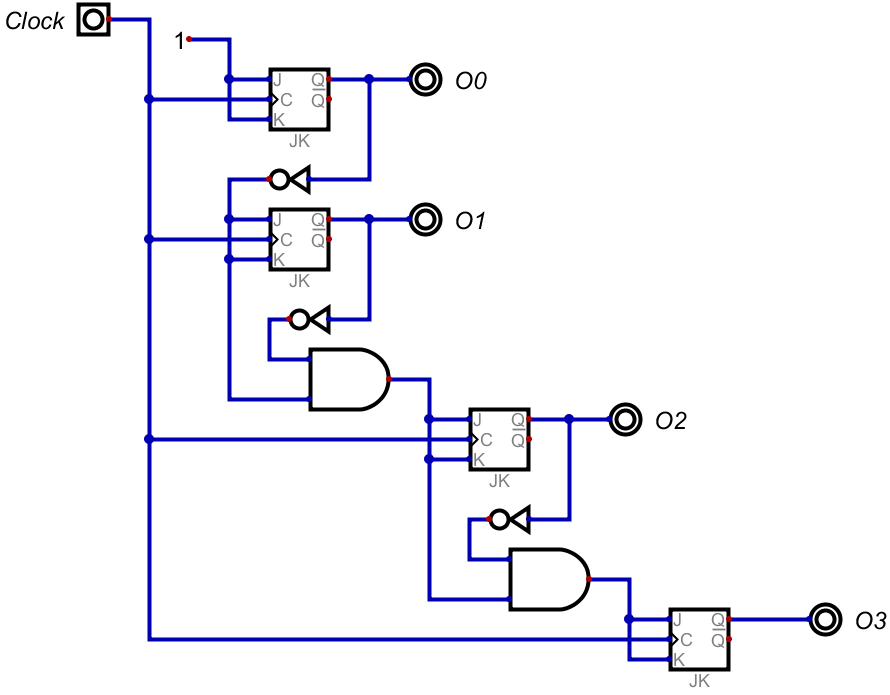
…なんかアップカウンタとの間違い探しみたいになっているが、NOT素子が3か所増えただけだ。
これだけで、ダウンカウンタの完成。
もちろんアップカウンタと同じく、同様の考え方で出力の数も増やせる。
アップダウンカウンタ
今紹介した二つのカウンタだが、スイッチか何かで動作を切り替えられると嬉しい。
ということで、それを実装してみよう。
上にも少し書いたが、これら二つの違いはシンプルで、各出力を上位桁の入力に入れる際に、それぞれNOTが入るかどうか。
つまり、そのまま入れればアップカウンタ、反転させればダウンカウンタになる、という考え方になる。
さて、この部分だけに注目して、一回真理値表を作ってみよう。
入力\(I\)の内容を、入力\(T\)によって操作することを考える。
\(T = 0\)の時は出力\(O\)は\(I\)と同じ、\(T = 1\)の時は\(O\)は\(NOT(I)\)とする。
これで真理値表を作ると…
| \(I\) | \(T\) | \(O\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
こうなる。
もうお馴染みだろう、XORだ。
というわけで、\(O = I \oplus T\)とすれば\(T\)による反転が実装できる。
これを、アップカウンタからダウンカウンタにするときにNOTを入れた部分に入れてあげれば、アップダウンカウンタの完成だ。
入力\(Mode\)を増やし、これによりアップとダウンを切り替えることにする。
0の時はアップカウンタ、1の時はダウンカウンタとして動作させよう。
これで回路を組むと、以下のようになる。
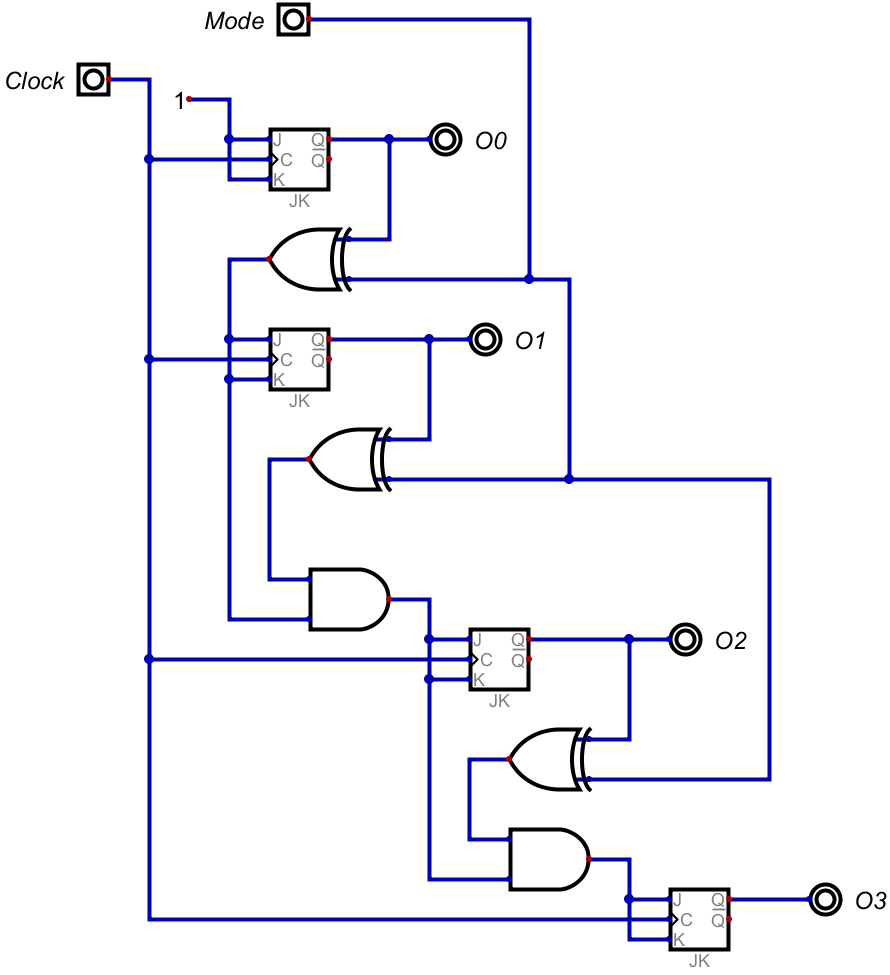
これで、アップダウンカウンタの基本形が完成だ。
もちろん、これも同じ考え方で桁数を増やせるので、必要に応じて増やしていこう。
乗算・除算の考え方
では、これを使ってどう乗算や除算を考えていくか…見ていく前に。
一つ、お詫びと訂正を。
以前やこの記事の冒頭で、乗算や除算もこのカウンタを使って実装すると書いた。
確かに実装できるし、その考え方はこれから解説する。
が、より効率のいい方法があったようなので、本シリーズで作成する電卓にはそちらを用いることにする。
紛らわしくて申し訳ないが、今回解説する内容はあくまで考え方の一つとしておいてほしい。
では、その方法を紹介しよう。
乗算
さて、まずは乗算、その意味から考えて…の前に。
今回実装する乗算は、入力・出力ともに負の数は考えない。
4桁で考えるが、例えば\((1000)_2\)は\(-8\)ではなく\(8\)として考える、ということだ。
では、改めて意味から考えてみよう。
例えば、\(2 \times 3\)について。
これは、2を3回足すと考えられる。
つまり、カウンタで3回カウントし、その1カウントごとに2を足していけばいい。
そのために、まずは結果保持用のJKフリップフロップを出力桁分用意する。
一旦、入力と同じ4桁で考えよう。
最初は全て0を保持している状態で、この出力と入力の片方を足す。
足す部分も以前作成した4桁加算器を使えばいい。
その出力をJKフリップフロップのJに入力し、Kにはその否定を入力。
これで、あとはクロック部分をなんとかすればいい。
そこで、カウンタの登場だ。
カウンタで数を足していき、もう一つの入力と同じになったらストップする、という考え方だ。
何かしらで同じかどうかを判定し、同じならクロック入力を0に固定すれば、そこで計算が終わる。
…逆に考えれば、違う間は1で、同じになったら0にすればいいのだ。
二つの入力が異なれば1になるというのは、そのままXORだった。
つまり、カウンタの出力ともう一つの入力それぞれでXORを取り、そのORを考えることで、異なれば1、同じなら0という出力が得られる。
あとは、これとクロックをANDで取れば狙ったところで止まるクロックの完成。
これを、各JKフリップフロップのクロック入力に入れればいい。
…と文章で書いてきたが、何が何やらよく分からないと思う。
そこで、サクッと回路を組んでみた。
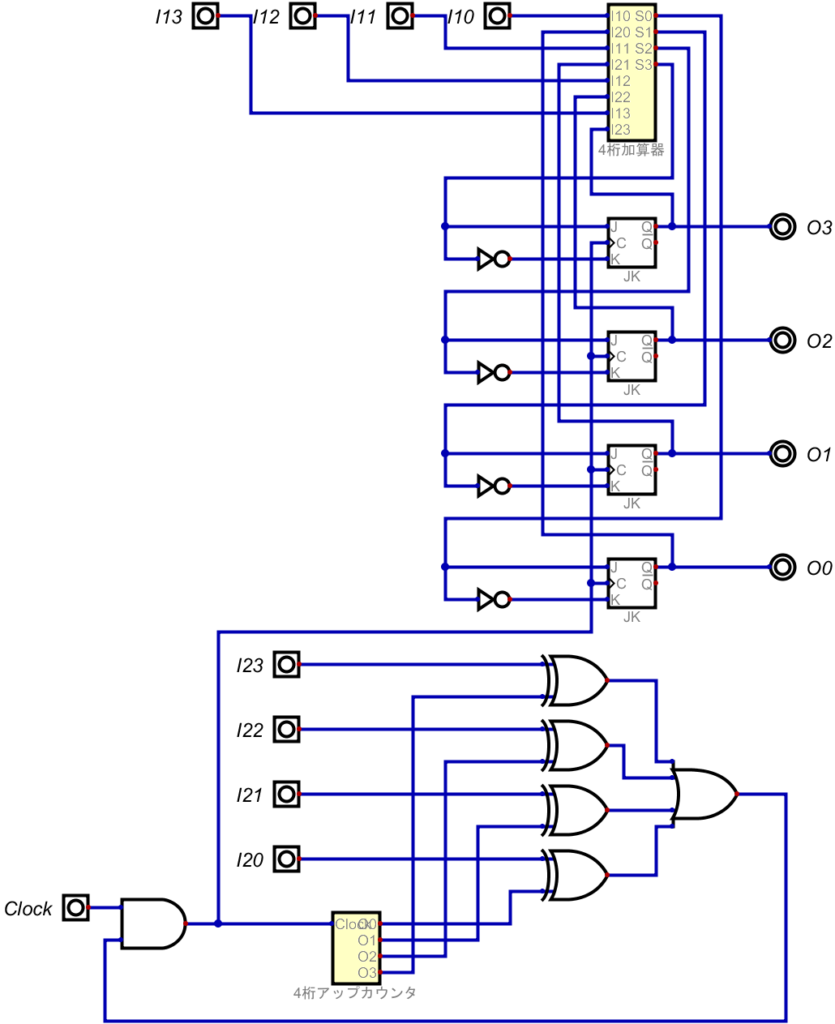
これで、この回路へのクロック入力を繰り返すことで、最終的に答えが得られる。
…が、これでは何クロックで答えが得られるかが計算によって変わってしまう。
それを解決する方法は次回紹介するので、本当は簡略化できないかも検討すべきだろうが…今回の乗算は一旦ここまでにしておこう。
除算
次は除算。
中身に入る前に、こちらも制限は4桁、正の数のみを考える。
また小数点以下は考えず、余りは別で表示させようと思えばできるが、本題で使わないものなのでとりあえず商だけ出せればOKとさせてもらう。
これも乗算と同じく、意味的に考えてみよう。
例えば\(5 \div 2\)といった場合。
これは、5から2を何回引けるかという考え方でいけそうだ。
つまり、被除数から除数を引くごとにカウンタをまわし、値がマイナスになれば…と思うかもしれないが、これだと上手くいかない。
なぜかというと、例えば\(9 – 1\)で考えてみる。
これを2進数で考えると、\(1001 – 0001\)となり、結果は\(1000\)だ。
値がマイナスになった部分と考えるとこの時点で止まり、商が1となってしまう。
ではどう考えるかというと、被除数が除数よりも大きい間、引くということが必要になる。
つまり、2値の大小比較が必要になるのだ。
というわけで、まずはそこから考えていこう。
二つの4桁2進数\(I_1 = I_{13} I_{12} I_{11} I_{10}\)、\(I_2 = I_{23} I_{22} I_{21} I_{20}\)を入力し、比較結果を出力する回路を作ってみる。
真理値表は…そのまま作ると256行になってしまうので、ちょっと考え方を変えてみよう。
まず、今回は正の値しか使わないので、上の桁から順番に見ていく。
もし\(I_{13} = 1\)かつ\(I_{23} = 0\)ならその時点で\(I_1\)の方が大きいことを出力。
逆に\(I_{13} = 0\)かつ\(I_{23} = 1\)ならその時点で\(I_2\)の方が大きいことを出力。
ここで\(I_{13} = I_{23}\)なら、一つ下の桁を見に行く。
そこからも同じ考え方で進んでいき、最後に\(I_{10} = I_{20}\)となったら、その時は\(I_1 = I_2\)なので1を出力する、という考え方になる。
で、考え方は上の桁から見たが、組む時は下の桁から見ていった方がいいだろう。
まず、\(I_{10}\)と\(I_{20}\)のみの比較を考える。
これを後で使いまわしたいので、入力は\(I_1\)、\(I_2\)としておく。
出力は三つ、\(I_1 > I_2\)の時のみ1となる出力、\(I_1 = I_2\)の時のみ1となる出力、\(I_1 < I_2\)の時のみ1となる出力。
先頭から順番に、\(A, B, C\)としておこう。
これで真理値表を作ると以下のようになる。
| \(I_1\) | \(I_2\) | \(A\) | \(B\) | \(C\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
\(B\)だけXORの否定を取り、他はそのまま普通に組めばいいだろう。
というわけで、これを組んだものが以下だ。
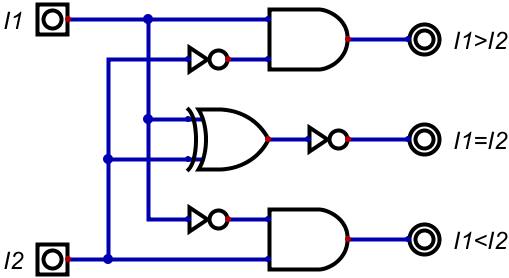
なお、出力は分かりやすいよう具体的にしておいた。
では、これを使って2桁に拡張しよう。
ここでは、上位桁の2値を同じように比較し、イコールなら下位の桁を出力に持ってきたい。
入力は4つ、\(I_1 = I_{11}I_{10}\)、\(I_2 = I_{21}I_{20}\)だ。
また、各桁に上でやった1桁の2値比較を通し、\(I_{11}\)と\(I_{21}\)の比較結果を\(A_1, B_1, C_1\)、\(I_{10}\)と\(I_{20}\)の比較結果を\(A_0, B_0, C_0\)としておく。
\(A, B, C\)は添え字が同じなら、いずれか一つのみ1となり、他は0となるので、それ以外は考えなくていい。
この条件で必要な部分だけ真理値表を書くと…
| \(A_1\) | \(B_1\) | \(C_1\) | \(A_0\) | \(B_0\) | \(C_0\) | \(A\) | \(B\) | \(C\) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
これを見ると、\(A\)から\(C\)は以下の論理式で表すことができる。
- \(A = A_1 + B_1A_0\)
- \(B = B_1B_0\)
- \(C = C_1 + B_1C_0\)
というわけで、組んだものが以下だ。
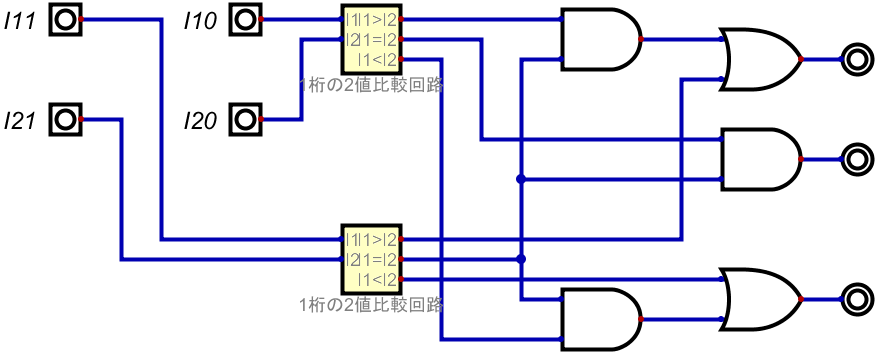
これで2桁の場合の比較回路ができた。
…さて、同じように3桁目を見ていってもいいのだが、何かお気づきだろうか。
今、下位の比較結果を用いて上位桁を実装した。
これが、そっくりそのまま次の桁にも使えるのだ。
つまり、今出した論理回路図の上の比較回路を2桁のものにすれば、今度は3桁の比較ができる。
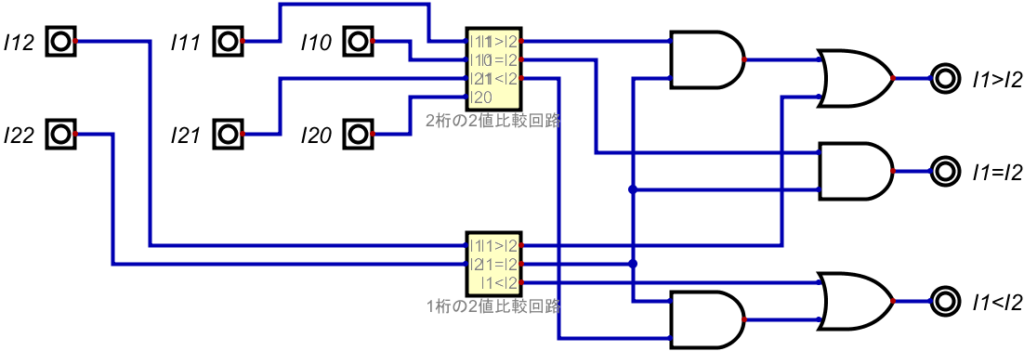
そして、さらにこれを使って、4桁の2値比較回路を作ると…
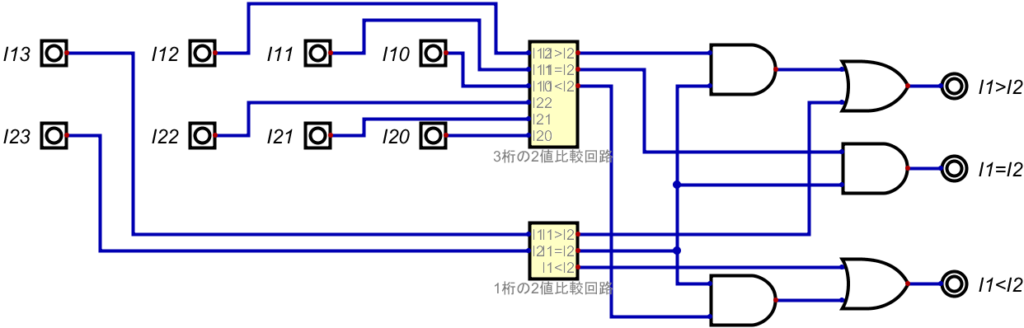
これで完成だ。
比較部分ができたので、本筋の割り算に戻ろう。
ここで、何回引けるかをさらに少し別の捉え方にしてみる。
上で作った乗算器を使って、何倍まで引けるかとしてみよう。
すると、割る数を何倍かしつつ、それが初めて元の数より大きくなった時の数から1を引けば、割り算の答えになる。
この方針で組んでみよう。
まず、割られる数を比較器の片方へ入力。
もう片方の入力には、割る数とカウンタ、乗算器を使って何倍かにできるようにしておく。
これで比較し、その結果が後者の方が小さくなったタイミングでクロックを受け付けなくし、その時のカウンタの値から1を引けば割り算の答えになる。
これを組んでみると以下の通りだ。
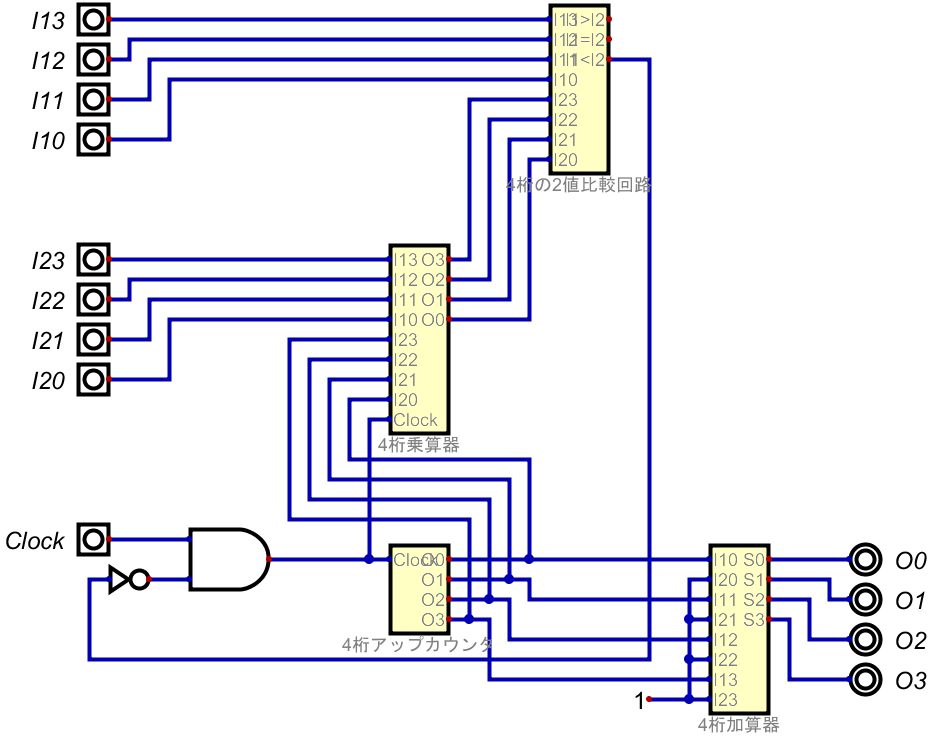
非常に大きくなってしまったが…一旦、これで加減乗除全てができるようになった。
とはいえ…やはりこれをこのまま使うのではなく、実際の電卓を組む際にはもっと別の方法を使うことにしよう。
おわりに
今回は…一応、最初はカウンタという回路を組もうという話で進めていた。
後半は一旦そのカウンタを用いた乗算・除算を行う回路を作成した。
が、まあ…見てもらえれば分かる通り、問題点も色々とある。
一番の問題は、答えが出るまでに複数のクロックが必要であること。
次回は、その問題点を解決すべく、1クロックでビシっと答えが出るような乗算・除算の回路を作成してみることにしよう。
代わりに回路規模がさらに大きくなりそうな気はしているが…まあ、頑張ってみる。
…もしかしたら、乗算と除算で回を分けるかもしれない。
2022/6/25追記
次回の内容、やはり2つに分けてまずは乗算回路を組合せ回路として作り直した。
思ったよりシンプルになり、かなりスッキリした。
…次々回の除算がどうなるか若干不安だが、なんとかやってみよう。





コメント