本シリーズでは、以下の本に沿って解説を書いている。

さて、前回から新しい単元である文脈自由文法に入った。
これまでの内容との違いに気を付けながら進めていこう。
以下がその記事だ。
今回は、この文脈自由文法…cfgにおける、幾つか重要な性質について紹介していく。
タイトルにも入れた、最左導出というやつと、導出木というやつだ。
最左導出
早速これから。
cfgで導出のステップを辿っているとき、複数の変数が出てくることがある。
前回の、正規表現の部分が分かりやすいだろう。
このような場合、どの変数から生成規則を使って置き換えても問題ない。
つまり、順番をどうしようが最終的に生成される列に変化はないのだ。
そのため、出てきた変数のうち、左から順番に置き換えをする、というルールを作ることができる。
このルールのことを、最左導出と呼ぶ。
さて、なぜこれが問題ないかだが、証明が二通り存在する。
まず、そのうち一つの証明をしていこう。
最左導出で問題ないことの証明その1
cfg\(G\)から列\(x \in \Sigma^*\)が生成できるとき、この\(x\)は最左導出によっても生成できることを示す。
なお、以下に出てくる文字について、\(x_1, x_2, x_3 \in \Sigma^*\)とする。
言い換えると、\(x_1, x_2, x_3\)には変数が出てこない。
また、生成規則\(A \rightarrow \alpha\)、\(B \rightarrow \beta\)となる\(\alpha, \beta \in (\Sigma \cup V)^*\)も用意しておこう。
まず、ステップを分解し、以下のような状態になっているとする。
$$\begin{eqnarray}
S & \overset{*}{\Rightarrow} & x_1Ax_2Bx_3 \\
x_1Ax_2Bx_3 & \Rightarrow & x_1Ax_2 \beta x_3 \\
x_1Ax_2 \beta x_3 & \Rightarrow & x_1 \alpha x_2 \beta x_3 \\
x_1 \alpha x_2 \beta x_3 & \overset{*}{\Rightarrow} & x
\end{eqnarray}$$
この導出の過程は、最左導出ではない。
…のだが、この2行目、3行目の導出は以下のように変更しても一切問題がないだろう。
$$\begin{eqnarray}
x_1Ax_2Bx_3 & \Rightarrow & x_1 \alpha x_2Bx_3 \\
x_1 \alpha x_2Bx_3 & \Rightarrow & x_1 \alpha x_2 \beta x_3
\end{eqnarray}$$
なぜかというと、生成規則は一つの変数を別の形に置き換えるものだったことを思い出そう。
つまり、それ以外には影響を与えない。
ということで、この流れに置き換えても全く問題ない。
そして、今\(A\)が最初に出てきた変数なので、最左導出のルールに沿う形にできた。
3つ以上の変数が登場している場合でも、まったく同じ議論ができる。
よって、最左導出という制限を付け加えても何の問題も生じないのだ。
最左導出で問題ないことの証明その2
こちらの方が分かりやすいかもしれない…
が、こちらには導出木を使う。
そのため、先に導出木の解説を見ていこう。
導出木
導出木とは、あるcfg\(G\)に対し、ある変数\(A \in V\)から具体的な列\(x\)を導出する際に用いられる、導出の様子を示した木構造のことだ。
この木構造が何ぞやという方も、今回に限ってはそこまで厳密な定義はいらない。
一応別で解説記事を書くつもりだが、ここの説明で分からないという場合だけで問題ないと思う。
その解説記事へのリンクは、公開したらここに貼ることにしよう。
では、詳細を説明していく。
具体例で見ていった方が分かりやすいと思うので、まずはその具体的なcfg\(G\)と列\(x\)を用意する。
cfg\(G = (V, \Sigma, P, S)\)は、以下のものを使う。
- \(V = \{S, A, B\}\)
- \(\Sigma = \{a, b\}\)
- \(P\)について
- \(S \rightarrow SS\)
- \(S \rightarrow \varepsilon\)
- \(S \rightarrow aB\)
- \(S \rightarrow bA\)
- \(A \rightarrow a\)
- \(A \rightarrow bAA\)
- \(B \rightarrow b\)
- \(B \rightarrow aBB\)
ちなみに、これが生成する言語は、記号\(\{a, b\}\)からなる列のうち、その\(a\)と\(b\)の個数が一致しているような列を含む。
これについて、列\(aaababbb\)の導出の様子を導出木で表してみよう。
まず、一番上に開始記号である\(S\)を置く。
その次に、生成規則の\(S \rightarrow aB\)を使う。
このとき、以下のように表す。
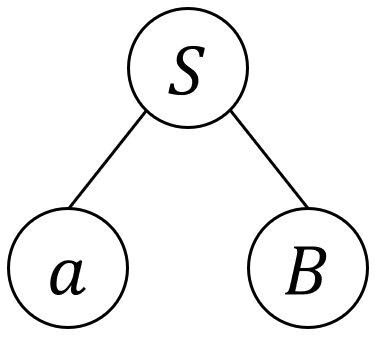
このように、ある変数を生成規則で置き換えたときに、置き換えた後の内容を下に繋げる。
このとき、一つの変数や終端記号を一つの点に置いてあげるのだ。
また、その点は、連接になっている順番で書く必要がある。
今回は、\(S \rightarrow aB\)という生成規則を適用して、\(S\)から\(a, B\)に続くように書いている、という感じになる。
さて、\(B\)はまだ変数で、ここも置き換える必要がある。
そのため、この\(B\)についても同じことをする。
これを、変数が無くなるまで繰り返してあげる。
先に、導出の様子を全部書いていこう。
赤字が、その回のステップで変化したところだ。
一応最左導出の形にもなっているので、それも併せて確認してみてほしい。
$$\begin{eqnarray}
\color{red}{S} & \Rightarrow & \color{red}{aB} \\
a\color{red}{B} & \Rightarrow & a\color{red}{aBB} \\
aa\color{red}{B}B & \Rightarrow & aa\color{red}{aBB}B \\
aaa\color{red}{B}BB & \Rightarrow & aaa\color{red}{b}BB \\
aaab\color{red}{B}B & \Rightarrow & aaab\color{red}{aBB}B \\
aaaba\color{red}{B}BB & \Rightarrow & aaaba\color{red}{b}BB \\
aaabab\color{red}{B}B & \Rightarrow & aaabab\color{red}{b}B \\
aaababb\color{red}{B} & \Rightarrow & aaababb\color{red}{b}
\end{eqnarray}$$
これを導出木で表すと、以下の通りだ。
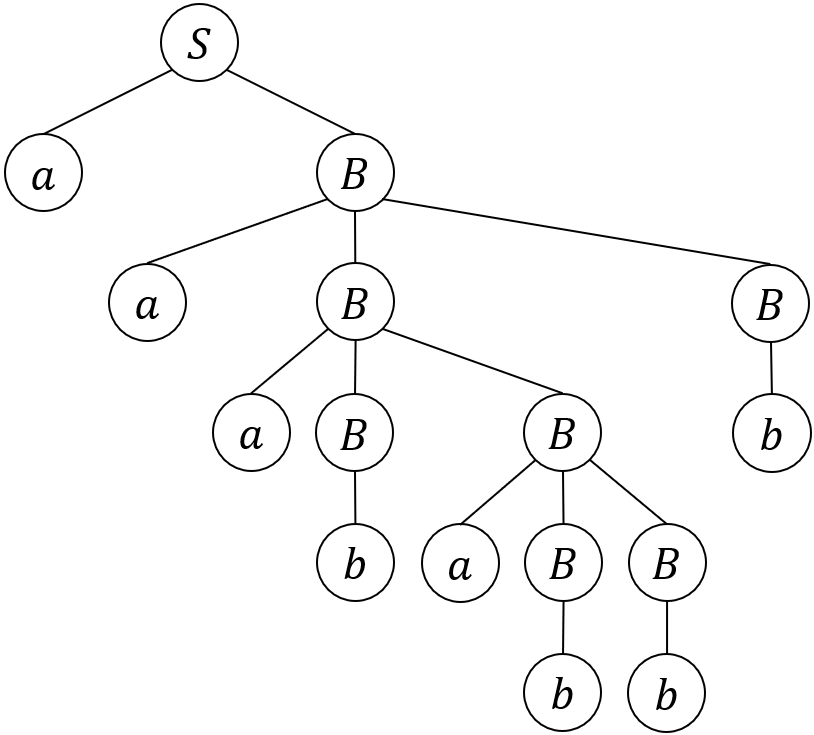
これで、末端の点が全て記号になっている。
ここまで来れば、あとは左から順番に記号を拾っていくことで、列を作ることができる。
これが、導出木というものだ。
最後の拾っていく順番が分かりづらい場合、終端記号の高さを以下のように揃えてあげると分かりやすいだろう。
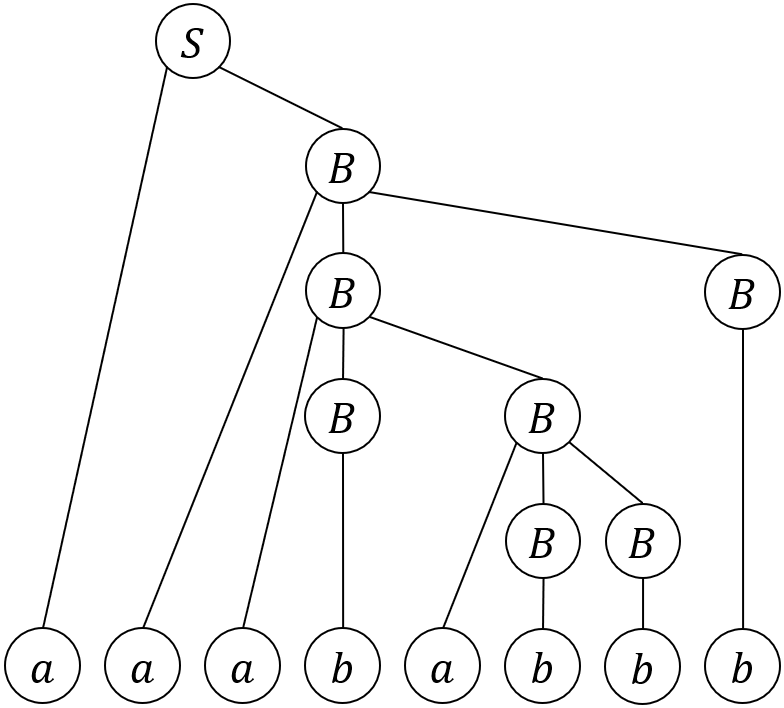
上で保留した証明
さて、この導出木を使って、最左導出で問題ないことの別証明を見ていこう。
とはいえ、非常に単純だ。
まず、上で出した導出木を見て欲しい。
これを、どういう順番で作成したかは分からないと思う。
最左導出というのは、それぞれの変数について、その下の部分をどういう順番で作るか、というルールに該当する。
しかし、例えば\(S \Rightarrow aB \Rightarrow aaBB\)の次のステップ、どちらの\(B\)を先に置き換えるかという情報が存在しない。
言い換えれば、どちらを先に置き換えても結果が変わらないことを示している。
よって、最左導出にしても問題ない、ということだ。
ちょっと感覚的な説明だが、ご理解いただけただろうか。
おわりに
今回は、cfgにおける最左導出と導出木を解説した。
これがあると分かりやすくなるので、覚えておくといいだろう。
さて、次回はこのcfgの能力について少し触れていこう。
前回の内容で、正規言語以外の言語もcfgで生成できる例を幾つかご紹介した。
では、正規言語ならcfgで生成できるのだろうか、という疑問が出てくる。
結論から言ってしまうと、正規言語はcfgで生成可能なのだが、それを次回証明していこう。
2021/1/27追記
次回の内容を更新した。
予告通り、正規言語はcfgで生成可能…言い換えると、正規言語は文脈自由言語であることを示した。
また、同時にdfaをcfgに変換する方法も解説している。
これで、以前の内容で正規言語をdfaで表し、それを使うことでcfgに直すことができるようにもなったはずだ。
ここはまだそんなに難しくないので、しっかり理解しておきたい。



コメント