前回は、自然言語処理における
意味理解の概要全体をお話した。
今回から、その詳細に入っていこう。
まずは、単語の意味理解の中でも、
概念体系やシソーラスといった
辞書の一種のようなものを扱う方法を説明する。
具体的なサイトも紹介するので、
よかったら触ってみて欲しい。
なお、本講座は以下の本を参考に進めている。
もしよかったら、中身を覗いてみて欲しい。
単語と概念の関係
まず、自然言語における単語と、
それが表す概念の関係について。
私たちが使っている日本語では、
単語について以下のようなパターンが存在する。
- 1つの単語が2つ以上の意味を持つ
- 2つ以上の単語が同じ1つの意味を持つ
上は多義語、下はその複数を同義語と呼んだりする。
意味というのは、
前回概念として扱うと解説した通り。
ということで、単語と概念には、
多対多の関係が成り立っていることになる。
例えば、「ドライバー」という単語に
注目してみよう。
この単語には、以下3つの概念が存在する。
- 車の運転手
- ゴルフ用品
- ねじ回し
さらに、一つ目は「運転手」、
三つ目は「ねじ回し」という単語が
そのまま同じ意味を持っている。
このように、単語と概念は多対多になっているのだ。
で、この概念を表すデータというものがあり、
それを集めたものを概念辞書と呼ぶ。
一番有名なのは日本語WordNetだろう。
私も大学の時研究で使ったことがある。
リンクを貼っておくので、気になったらいじってみてほしい。
概念の体系化とシソーラス
概念間の関係では、よく上下関係を考える。
2つの概念\(X\)、\(Y\)について、
「\(X\)は\(Y\)の一種である」とした場合、
\(X\)は\(Y\)の下位概念、
逆に\(Y\)は\(X\)の上位概念となる。
つまり、含まれる要素を下位に、
含む集合を上位に考えるのだ。
こう書くと、図にすれば綺麗な木構造になりそう…
なのだが、実は
「\(X\)は\(Y\)の一種で、かつ\(Z\)の一種である」
といった関係もある。
具体的に言うと、
「犬」は「イヌ科の動物」の下位であると同時に、
「家畜」の下位でもある。
そのため、木構造にはならないので注意が必要だ。
具体例でさらっと使ってしまったが、
通常は各概念に、それを表す一つの単語を
対応付けている。
つまり、単語的に見ると、
概念によって階層構造が出来上がっているのだ。
この、単語が意味内容によって
分類されている辞書のことを、シソーラスと呼ぶ。
実は、上で紹介した日本語WordNetは
このシソーラスになっている。
ちょっと、日本語WordNetでのお話をしておこう。
日本語WordNet
上で紹介したように、日本語WordNetは、
概念を単語によってラベル付けし、
それを階層的に分類したシソーラスだ。
ただ、ここでの単語は一つではなく、
同義語の集合として割り当てられている。
この集合のことをsynsetと呼んでいる。
例えば、「自動車を運転する人」という
概念に対応づけられているsynsetは…
- ドライバー
- 運転者
- ドライバ
- ドライヴァー
- 運ちゃん
- 運転手
となっている。
そして、上でも書いたように、
この「ドライバー」という単語は、
他のsynsetにも含まれている。
というように、日本語WordNet内では、
一つの概念に対応するのは
1つのsynsetであることに注意してほしい。
類似度
ここで、このシソーラスを使って
類似度という数値を定義してみよう。
これはそのままの意味で、
二つの概念がどの程度似ているか
というものを数値で表したもの。
考え方としては、どの程度上に辿れば
同じ概念にたどり着くかというものだ。
少ない経路でたどることができれば似ているし、
経路が長いとあまり似ていないという感じだ。
ただ、相対的な長さだけでは不十分なことがある。
というのも、シソーラスの上位には
非常に広範囲の内容を表す概念があり、
下位には細かい範囲の内容を表す概念がある。
一つで辿れるからといって、
それが広範囲だとあまり似ているとは言えないだろう。
そこで、絶対的な位置を考慮する考え方が出てきた。
「ウーとパルマーによる類似度の定義」というものをご紹介しよう。
これは、各概念の根からの深さで、類似度を定義する。
二つの概念\(w_1\)、\(w_2\)の類似度を求めるとする。
このとき、この二つに共通する上位概念で、
最も深くにある…根からの距離が長いものを
\(LCS\)と呼ぶ。
これはLeast Common Superconceptの略だ。
また、\(\mbox{depth}(w)\)は、
概念\(w\)の深さとしよう。
このとき、二つの概念の
類似度\(\mbox{similarity}(w_1, w_2)\)は、以下式で定義される。
$$\mbox{similarity}(w_1, w_2) = \frac{\mbox{depth}(LCS) \times 2}{\mbox{depth}(w_1) + \mbox{depth}(w_2)}$$
具体的に計算してみよう。
例えば、以下のようなシソーラスだったとしよう。
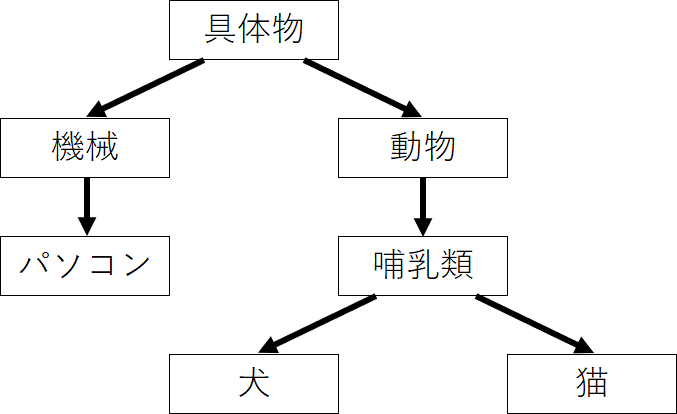
根を「具体物」とし、
まずは「犬」と「猫」の類似度を求めるとする。
\(LCS\)は「哺乳類」だ。
それぞれの深さを見ると、
哺乳類は2、犬と猫は3なので、計算すると…
$$\frac{2 \times 2}{3 + 3} = \frac{4}{6} \sim 0.67$$
こうなる。
また、例えば「犬」と「パソコン」で見てみよう。
この二つの\(LCS\)は根の「具体物」となる。
この深さは0なので、分母が0、
つまり類似度も0だ。
これができると何が嬉しいかだが、
単語のクラスタリングや類似性判定に使える。
さらに、それを基にして
文や文章の類似度計算にも応用可能だ。
問題点
いいことばかりではない。
これは、シソーラスありきで行っているが、
そのシソーラスで全ての概念が
網羅できていることはないだろう。
つまり、網羅性に欠けてしまう。
また、言語はときに変化する。
新しい言葉が生まれることだってあるだろう。
そういった変化への対応にも、
かなりコストがかかる。
もう一つ、同じ単語でも分野によって
意味が変化したりする。
こういった階層構造を作る際には、
一つに観点を絞り込む必要があるが、
それも実際難しい問題だ。
こういった問題を回避するために、
シソーラスの代わりにコーパスを用いる方法が挙げられる。
実際にどのような使われ方をしているかに
着目するのだ。
それが、次回以降の内容となる。
おわりに
今回は具体的な単語の意味…
概念の階層化を行ったシソーラスと、
それを使った類似度という数値の計算方法をご紹介した。
とはいえ、このままでは問題もあるので、
次回以降で別の手法を見ていくこととしよう。



コメント