本シリーズでは、以下の本に沿って解説を書いている。

前回は、二つ目の標準形であるグライバッハ標準形を紹介した。
変換方法が複雑、かつそれによってできる生成規則の数もかなり増えるので、幾つか具体的な例を使って練習しておきたい。
以下がその記事だ。
さて、今回は標準形から離れる。
ある言語が、文脈自由文法であるかどうかを判別するための道具の一つを紹介していこう。
参考書では\(uvwxy\)定理と書かれているが、他では反復補題と呼ばれているところもある。
毎回呼び方を変えていると混乱するので、本記事では参考書に合わせて\(uvwxy\)定理と呼ぶことにしよう。
具体例も交えながら、しっかり見ていこう。
生成する列が有限の言語
定理に入る前に、参考書には載っていないが少し補足をしておこう。
ある言語\(L\)について、それに含まれる列の数が有限だとする。
このとき、その言語は必ず文脈自由言語である。
言い換えると、\(L = L(G)\)となるcfg\(G\)が存在する、ということだ。
この証明は非常に簡単。
まず、前提から言語\(L\)は有限なので、具体的に列を書き上げることができる。
今、\(L = \{x_1, x_2, …, x_n\}\)、\(x_i \in \Sigma^*\)だったとしよう。
このとき、cfg\(G = \{V, \Sigma, P, S\}\)を以下のように定義する。
- \(V = \{S\}\)
- \(P\)について
- \(S \rightarrow x_1\)
- \(S \rightarrow x_2\)
- …
- \(S \rightarrow x_n\)
簡単に言ってしまうと、言語に含まれる列が有限なので、その全てを直接生成するような生成規則を作ってしまえばいい。
こうすると、今全ての列\(x_i \in L\)に対して以下のステップが存在する。
$$S \Rightarrow x_i$$
そして、どの生成規則の右側にも変数が登場していない。
つまり、これで\(L(G) = \{x_1, x_2, …, x_n\}\)だと分かるので、証明完了だ。
これで、言語が有限個の列しか含まなかったら、その時点で文脈自由言語であることが分かった。
…なぜこんな補足をしたかというと、定理が有限個でないような言語を対象にしているからだ。
とはいえ、通常は有限個であることは少ないだろう。
\(uvwxy\)定理(仮の姿)
では、本題に入ろう。
なんか仮の姿とか入っているが、その詳細は具体例でお見せする。
列の数が有限でないような文脈自由言語\(L\)について考える。
このとき、まずその言語\(L\)によって、ある定数\(K\)が存在する。
そして、\(|z| \geq K\)となる任意の列\(z \in L\)に対し、以下三つの条件を満たす5つの列\(u, v, w, x, y\)が存在する。
- \(z = uvwxy\)
- \(vx \not = \varepsilon\)
- 任意の\(i \geq 1\)に対し、\(uv^iwx^iy \in L\)
…何を言っているか分かるだろうか。
少なくとも、これだけだと私もよくわからなかった。
というわけで、証明の前にこれの使い方を見ていこう。
まず、背理法で今調べたい言語が文脈自由言語であると仮定する。
次に、条件を満たさないような列が一つでも存在することを導く。
すると、上の定理と矛盾が発生するので、\(L\)は文脈自由言語ではない、ということが示せるのだ。
これを使って、幾つか具体例で示してみよう。
具体例その1
まず、言語\(L\)を以下のように定義する。
$$L = \{a^nb^nc^n | n \in \mathbb{N}\}$$
幾つか具体的に列を書いてみると、\(abc\)、\(aabbcc\)、\(aaabbbccc\)、などなど。
このように、\(a\)、\(b\)、\(c\)がその順番で、同じ数ずつ連続するような列を集めた言語だ。
これは、文脈自由言語ではない。
それを、上の定理で示してみよう。
まず、背理法でこの\(L\)が文脈自由言語であると仮定する。
この\(L\)は\(n\)の値を変えることで無限個の列を作ることができるので、\(uvwxy\)定理の前提を満たすことになる。
つまり、その後半の条件を満たすはず。
\(K\)の具体的な値について…は、今はまだ分からない。
しかし、その\(K\)がどんな値だろうと、それ以上の長さの列を用意することはできる。
例えば、列\(z = a^Kb^Kc^K\)。
これは、\(a\)、\(b\)、\(c\)それぞれが\(K\)個並んでいるので、長さは\(3K\)、\(K\)以上である。
これで、\(K\)がどんな値だろうと問題なく以下の議論を行うことができる。
\(uvwxy\)定理によれば、この列\(z\)は条件2と3を満たすように5つの列\(u, v, w, x, y\)に分解できる。
条件2から、\(vx \not = \varepsilon\)なので、\(v \not = \varepsilon\)としておこう。
では、この\(v\)の取り方で場合分けをしていく。
まず、\(v = a^ib^j\)、\(i, j > 0\)としてみよう。
このとき、\(u = a^{K – i}\)、\(wxy = b^{K – j}c^K\)となっている。
イメージは以下のような感じだ。
$$\underbrace{aa…a}_{u} \underbrace{aa…abb…b}_{v} \underbrace{bb…bcc…c}_{wxy}$$
このとき、\(uv^2wx^2y\)という列を見てみると、明らかに…
$$\underbrace{aa…a}_{u} \underbrace{aa…abb…b}_{v} \underbrace{aa…abb…b}_{v} …$$
というように、\(b\)の後に\(a\)が出てきてしまう列になる。
これは、言語\(L\)には含まれない形だ。
\(v = b^ic^j\)、\(i, j > 0\)の時も同様。
では、\(v\)の取り方を変えてみる。
今度は、\(v = a^i\)、\(i > 0\)としてみよう。
このときの様子は以下の通りだ。
$$\underbrace{aa…a}_{u} \underbrace{aa…a}_{v} \underbrace{aa…abb…bcc…c}_{wxy}$$
さらに、ここから\(x\)の取り方で場合分けをしていきたい。
このとき、一つ目のパターンと同じ理由で、\(x\)は記号の切り替わりの部分を含むことはできない。
そのため、\(x = \varepsilon\)、\(x = a^j\)、\(x = b^j\)、\(x = c^j\)のいずれかになる。
一つ目、\(x = \varepsilon\)のとき。
これで列\(uv^2wx^2y = uv^2wy\)を見てみると、\(a\)の数が他二つより\(i\)個増えてしまう。
二つ目、\(x = a^j\)、\(j > 0\)のとき。
同じくこれで列\(uv^2wx^2y\)を見ると、\(a\)の個数は\(K\)より大きいのに、\(b\)、\(c\)の個数が\(K\)個のまま。
三つ目の\(x = b^j\)、\(j > 0\)と四つ目の\(x = c^j\)、\(j > 0\)も今度は\(x\)ではない方だけ\(K\)個なので、おかしくなってしまう。
よって、\(v\)の取り方はこれも違う。
…ここまで来ると、あとはもう分かると思う。
残っている\(v\)の取り方は、\(v = b^i\)、\(v = c^i\)のいずれか、両方とも\(i > 0\)だ。
このとき、列\(uv^2wx^2y\)を作ると、明らかに\(a\)の個数が\(K\)個で、他二つの少なくともどちらかは\(K\)個よりも大きくなってしまう。
以上から、\(v\)をどのように取ったとしても、\(uv^2wx^2y \not \in L\)となった。
しかし、\(uvwxy\)定理から、この列は、\(L\)に属するはず。
これで、矛盾を導き出せた。
何がまずかったかというと、最初に\(L\)が文脈自由言語であると仮定したところ。
よって、\(L\)は文脈自由言語ではない、以上で証明完了だ。
…なんとなく、使い方は分かっただろうか。
具体例その2
では、二つ目の具体例として以下の言語で見てみよう。
$$L = \{zz | z \in {a, b}^*\}$$
これは、\(a\)と\(b\)からなる列のうち、2回同じ並びを繰り返すような列からなる言語だ。
これも\(uvwxy\)定理を使ってみよう。
まず、これを文脈自由言語と仮定する。
ある\(K\)より長い列、今回は…と進みたいところだが。
実は、今回は証明することができない。
なぜなら、\(u = w = y = \varepsilon\)、\(v = x = z\)とすることで、どんな\(i > 0\)に対しても\(uv^iwx^iy = v^ix^i \in L\)が言えてしまう。
つまり、上の\(uvwxy\)定理の内容ではまだ不十分、これが仮の姿と言った理由だ。
これを調整して、本当の姿をお見せしよう。
\(uvwxy\)定理
ここからがメインの内容となる。
前提は同じくある言語\(L\)は有限でない文脈自由言語である、というもの。
このとき、ある定数\(K\)が存在し、長さが\(K\)以上の列\(z \in L\)に対して以下4つの条件を満たすような5つの列\(u, v, w, x, y\)が存在する。
- \(z = uvwxy\)
- \(vx \not = \varepsilon\)
- 任意の\(i \geq 1\)に対し、\(uv^iwx^iy \in L\)
- \(|vwx| \leq K\)
一つだけ、4つ目の条件を追加した。
これが、\(uvwxy\)定理の真の姿だ。
さっき示せなかった具体例の証明
では、これを使ってさっき示せなかった具体例を証明していこう。
言語\(L\)は以下の通りだった。
$$L = \{zz | z \in {a, b}^*\}$$
さっきやりかけたように、まずはこれを文脈自由言語と仮定する。
そして、\(K\)以上の長さの列について、\(m \geq K\)として\(z = a^mb^ma^mb^m\)と取る。
長さ\(K\)以上の列が4つ繋がっているので、明らかに全体も長さは\(K\)以上だ。
これを5つの列に分解していくのだが、今新しく追加された4つ目の条件から、\(|vwx| \leq K\)でなければいけない。
これを守ろうとすると、\(vwx\)の部分は以下のいずれかになる。
- \(a\)もしくは\(b\)が連続している部分
- \(a\)もしくは\(b\)が続き、途中で他方に入れ替わってそれが続く部分
一つ目のパターンでは、\(v\)と\(x\)は必ず一つの終端記号が続くような状態になる。
これもイメージを出してみよう。
$$\underbrace{aa…abb…b}_{u} \underbrace{bb…b}_{vwx} \underbrace{bb…baa…abb…b}_{y}$$
今は前半の\(b\)のところと仮定しているが、他でも同じだ。
このとき、\(uv^iwx^iy\)は、その\(vwx\)が属している部分の文字だけが増えてしまい、同じ列の繰り返しとはならなくなる。
二つ目、これは以下のようなイメージ。
$$\underbrace{aa…abb…b}_{u} \underbrace{bb…baa…a}_{vwx} \underbrace{aa…abb…b}_{y}$$
このときも、\(v\)と\(x\)の少なくとも一方は空列ではないので、それらの取り方によらずに\(uv^iwx^iy\)が言語\(L\)の条件を満たさなくなる。
\(v\)が空列でないとすると、\(v\)は少なくとも\(b\)一個は入っている。
つまり、\(i = 2\)とすると前半の\(b\)の個数が増えてしまう。
これは\(v\)の取り方…もっと言うと\(vwx\)の取り方を変えても全て同じように示せる。
以上で、この列\(a^mb^ma^mb^m\)は条件を満たさないので、矛盾。
言語\(L\)は文脈自由言語ではないことが示せた。
\(uvwxy\)定理の証明
では、\(uvwxy\)定理の証明をしていこう。
まず、前提からある言語\(L\)を有限でない文脈自由言語とする。
このとき、文脈自由言語の定義と以前証明した内容から、この言語から空列\(\varepsilon\)を除いた部分を生成するようなチョムスキー標準形のcfg\(G = (V, \Sigma, P, S)\)が存在する。
チョムスキー標準形を軽く復習しておこう。
生成規則が以下3パターンのいずれかであるとき、チョムスキー標準形であると定義していた。
- \(S \rightarrow \varepsilon\) ※\(S\)は生成規則、今回はこれを含まない
- \(A \rightarrow BC\) ※\(A, B, C \in V\)
- \(A \rightarrow a\) ※\(A \in V\)、\(a \in \Sigma\)
また、任意のcfgはチョムスキー標準形に変形できたことも思い出そう。
詳細は以下の記事を参照してほしい。
この\(G\)で、ある列\(z\)についての導出木を作ることを考える。
導出木は以下の記事で解説していた。
続きの話をする前に、必要な概念があるので定義しておこう。
導出木において、高さという考え方を導入する。
これは、導出木の一番上の変数から、一番下の終端記号まで辿る時に通った線の数のうち、一番大きいものだ。
例えば、以下の導出木。
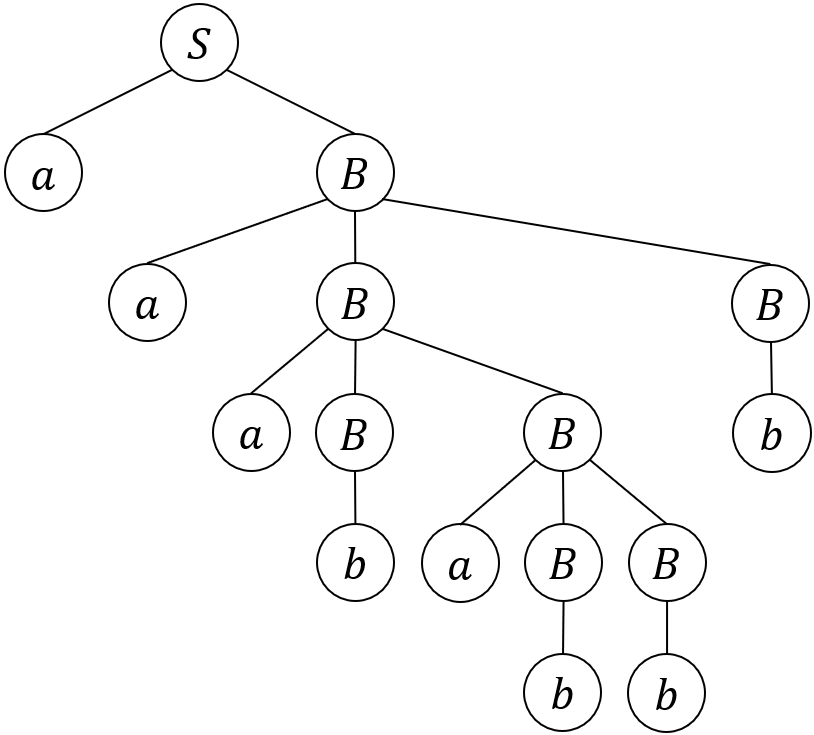
過去に導出木のところで出した例だが、この導出木の高さは5となる。
一番上の\(S\)から、右、真下、真下、右、真下or右、真下と進めば、最大の経路になる。
このとき通った線の数が5本なので、この導出木の高さが5になるのだ。
…高さの定義が終わったところで、本題に戻ろう。
今\(G\)はチョムスキー標準形なので、導出木においては全ての変数から以下の2パターンしか下に要素を繋げることができない。
- 二つの変数
- 一つの終端記号
このことから、ある導出木の高さを\(h\)以下と置くと、その導出木で表現されている列の長さは、最大でも\(2^{h – 1}\)となる。
これを、\(h\)に関する帰納法で示そう。
まず\(h = 1\)の時。
導出木は、上に開始記号、そのすぐ下に一つの終端記号の形しかあり得ない。
つまり、この時の列は長さが最大でも1になる。
\(2^{h – 1}\)を計算すると…
$$2^{h – 1} = 2^{1 – 1} = 2^0 = 1$$
より、問題ない。
次に、高さがある数\(k = h – 1 > 1\)までで成り立っていると仮定する。
これで、高さが\(k + 1\)を見てみる。
\(k + 1 > 2\)、かつcfgがチョムスキー標準形なので、開始記号からは必ず二つの変数で分かれていることがわかる。
その分かれた先それぞれを切り取って、二つの導出木として見てみよう。
すると、それぞれの高さは\(k\)以下となっており、帰納法の仮定を満たす。
つまり、そのそれぞれの部分で表現されている列の長さは、最大でも\(2^{k – 1}\)なのだ。
一番大きいパターン、二つの導出木両方が長さ\(2^{k – 1}\)の列を表現しているとしてみる。
すると、元の高さ\(k + 1\)の導出木によって表現されている列の長さは…
$$2^{k – 1} + 2^{k – 1} = 2 \times 2^{k – 1} = 2^{k – 1 + 1} = 2^k$$
ということで、最大でも\(2^k\)となる。
これで条件を満たすことが分かったので、成立だ。
さて、今注目しているcfg\(G\)に話を戻す。
この\(G\)の変数の数を\(k\)としたとき、\(K = 2^k + 1\)とおく。
ネタバレをしてしまうと、この\(K\)は定理に出てきていた\(K\)そのものだ。
ある列\(z \in L\)について、\(|z| \geq K\)のとき、\(|z| \geq 2^k + 1 > 2^k\)。
これで、今示した内容より、\(z\)を表現している導出木の高さは\(k + 1\)以上となる。
このとき、その高さを求めるために通った経路を見てみよう。
この中には変数や終端記号を表す丸が\(k + 2\)個以上含まれており、その一番下のみが終端記号、他は全て変数。
つまり、経路内には\(k + 1\)個以上の変数が含まれていることになる。
変数を\(k\)個としていたので、鳩ノ巣原理からその経路においてある変数\(A \in V\)が必ず2回以上登場することがわかる。
その同じ変数\(A\)を表す丸二か所について、以下の条件を満たしている部分を持ってくることができる。
- 片方は、必ず他方よりも開始記号に近い
- 開始記号に近い方から終端記号まで、線の数が\(k + 1\)以下で辿れる
二つ目について軽く補足。
ここで線の数が\(k + 2\)以上あったとすると、その時注目しようとしていた変数については成り立たないかもしれないが、他の変数ではやはり鳩ノ巣原理から同じ変数が2回以上登場することになる。
今度はその変数に注目を切り替えれば、この条件を満たす部分を必ず持ってこれるのだ。
さて、今開始記号に近い方の変数を改めて出発点とすると、その導出木が表現するのは長さが\(2^k\)以下の\(z\)の部分列\(z_1\)となる。
他方の変数を出発点としたときの導出木が表現する列を\(w\)としよう。
このとき、\(z_1 = vwx\)と表すことができ、\(vx \not = \varepsilon\)だ。
この理由について、今注目している変数を\(A\)とする。
このとき、\(z_1\)を表現している導出木の出発点は、例えば\(A \rightarrow BC\)のような生成規則を元にしている。
そして、その導出の中でもう一回\(A\)が出てきているということは…
$$A \Rightarrow BC \overset{*}{\Rightarrow} vAx \overset{*}{\Rightarrow} vwx$$
のようなステップが存在することになる。
さらに、この\(w\)は、\(B\)と\(C\)いずれかから導出される列に含まれている。
その上、今回はチョムスキー標準形なので、\(B\)、\(C\)から導出される列はいずれも空列ではない。
よって、\(z_1 = vwx\)、\(vx \not = \varepsilon\)となる。
ということは、だ。
先ほど出したステップの3番目に書いた\(vAx\)の\(A\)から、さらに\(vAx\)を導出するステップも存在する。
$$vAx \overset{*}{\Rightarrow} vvAxx = v^2Ax^2$$
そして、これを繰り返せばどんな\(i > 0\)に対しても、\(v^iAx^i\)という列を作り出すことができ、最終的に…
$$v^iAx^i \overset{*}{\Rightarrow} v^iwx^i$$
という列がその部分で導出できることになる。
また、同時に\(|vwx| = |z_1| = 2^k < K = 2^k + 1\)もこの中で言えている。
大元に話を戻そう。
今、列\(z\)の部分列\(z_1\)について話をしていた。
つまり、その前後に列\(u, y\)をつけてあげれば…
$$z = uz_1y = uvwxy$$
となり、これで証明完了だ。
…と思いきや、一つだけ残っている。
4つ目の条件について、今示したのは\(|vwx| < K\)。
定理にはイコールも入っているのは何なのだ、という部分。
実は今回の証明も参考書以外の内容を色々参照していたのだが、そのいずれにもこの答えになりそうな内容の記載はなかった。
この差は、証明でチョムスキー標準形を仮定していたことにより生じていると思っている。
というのも、チョムスキー標準形を仮定すると、\(u\)もしくは\(y\)が空列ではない、という条件も追加されてしまうのだ。
これは先ほど\(v\)もしくは\(x\)が空列でないことを示した箇所と同じ方法で示せる。
しかし、この証明はチョムスキー標準形を仮定しなくとも(細かい数字は変わってくるが)同じ流れで行うことができる。
その際は、\(u\)と\(y\)の両方が空列でも問題なくなり、その関係で\(|vwx| = K\)となるパターンも出てくるのだろう。
申し訳ないが、ちょっとここで力尽きてしまったので、これ以上の内容はパスさせてもらう。
ただ、どの内容を参照しても今回紹介した形で載っていたので、定理に誤りはないはずだ。
おわりに
今回は、\(uvwxy\)定理、あるいは反復補題というものを紹介した。
ちょっと課題が残ってしまったが、後日やる気が回復したら取り掛からせてもらうことにしよう。
ちなみに、一つだけ注意があり、これを使えばどんな文脈自由言語でない言語でもそのことを示せるわけではない。
今はあくまで、文脈自由言語なら条件を満たすよ、ということを言っているだけで、条件を満たせば文脈自由言語である、とは言っていない。
実際に、定理の条件を満たしつつ文脈自由言語ではない例も存在するようなので、そこは気を付けておこう。
さて、次回は新しい単元に入る。
前にも名前だけ出していたが、プッシュダウンオートマトンというものだ。
以前扱っていたオートマトンに似ているが、少し変わっている部分ももちろんあるので、混同しないよう気を付けながら進めていこう。
2021/2/8追記
次回の内容であるプッシュダウンオートマトンの解説を公開した。
参考書と少し定義を変えているので、そこだけ気を付けながら読み進めていただきたい。




コメント